| 3. Отношения между множествами. Отношения между множествами наглядно представляют с помощью особых чертежей, называемых кругами Эйлера. Для этого множества представляют в виде кругов (овалов). В начальном курсе математики с понятием подмножества млад- шие школьники встречаются, выполняя, например, задания: «Назо- ви среди данных чисел четные», «Среди данных четырехугольников найди прямоугольники». 4. Пересечение множеств. Пересечением множеств A и B называют множество, содержа- щее те и только те элементы, которые принадлежат множеству A и множеству B. Если изобразить множества A и B с помощью кругов Эйлера, то пересечением данных множеств является заштрихованная область. В том случае, когда множества A и B не имеют общих элементов, говорят, что их пересечение пусто и пишут: пересечение а и б пустое множество. 5. Объединение множеств. Объединением множеств A и B называют множество, содер- жащее те и только те элементы, которые принадлежат множеству A или множеству B. Если изобразить множества A и B с помощью кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью 6. Свойства пересечения и объединения множеств. Если обратиться к определениям пересечения и объединения множеств, то можно увидеть, что в них не фиксируется порядок оперирования множествами. Например, выполняя объединение, можно к элементам одного множества присоединить элементы другого, а можно поступить наоборот: к элементам второго множества присоединить элементы первого. Аналогичная ситуация и в случае, когда выполняется пересечение множеств. Это означает, что пересечение и объединение множеств обладают переместительным, или, как говорят в математике, коммутативным, свойством. Пересечение и объединение множеств обладают также сочетательным, или ассоциативным, свойством. Взаимосвязь пересечения и объединения множеств отражается в распределительных, или дистрибутивных, свойствах этих операций: Пересечение дистрибутивно относительно объединения множеств. Объединение дистрибутивно относительно пересечения множеств. 7. Разность множеств. Разностью множеств A и B называют множество, содержащее те и только те элементы, которые принадлежат множеству A и не принадлежат множеству B. Если представить множества A и B с помощью кругов Эйлера, то разность A \ B изобразится заштрихованной областью. Если элементы А и В перечислены, то, чтобы найти А \ В, до- статочно перечислить элементы, которые принадлежат множеству А и не принадлежат множеству В. Если множества А и В заданы характеристическими свойствами, то характеристическое свойство множества A \ B будет таким: «со- стоять из таких элементов, которые принадлежат множеству А и не принадлежат множеству В». Разность множеств обладает рядом свойств. В частности, для любых множеств A, B и C справедливы следующие равенства: 1) (A \ B) \ C = (A \ C) \ B; 2) (A  B) \ C = (A \ C) B) \ C = (A \ C)  (B \ C); (B \ C); 3) (A \ B)  C = (A C = (A  C) \ (B C) \ (B 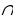 C); C); 4) A \ (B 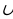 C) = (A \ B) C) = (A \ B) 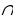 (A \ C); (A \ C); 5) A \ (B 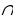 C) = (A \ B) C) = (A \ B)  (A \ C). (A \ C). 8. Дополнение множеств . Дополнением подмножества B до множества A называют множество, содержащее те и только те элементы множества A, которые не принадлежат множеству B. Если элементы множеств A и B перечислены, что- бы найти дополнение множества B до множества A, достаточно перечислить элементы, принадлежащие множеству A и не принадлежащие множеству B. 9. Декартово произведение. Декартовым произведением множеств A и B называют множество всех пар, первая компонента которых принадлежит множеству A, а вторая — множеству B. Упорядоченные наборы часто называют кортежами и различают по длине. Длина кортежа — это число элементов, из которых он состоит. Например, (3, 6, 7) — это кортеж длины 3, (м, а, т, е, м, а, т, и, к, а) — это кортеж длины 10. Декартовым произведением множеств A1, A2, …, An называют множество всех кортежей длины n, первая компонента которых принадлежит множеству A1, вторая — множеству A2, …, n-я — множеству An. 10.Число элементов в декартовом произведении конечных множеств. Нам известно, как находят декартово произведение конечных множеств. Например, если A = {x, y, z}, B = {m, p}, то A х B ={(x, m), (x, p), (y, m), (y, p), (z, m), (z, p)}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?» — достаточно пересчитать их. А как определить число элементов в декартовом произведении множеств, не образуя его и не обращаясь к пере- счету элементов? Доказано, что если в множестве A содержится а элементов, а в множестве B — b элементов, то в декартовом произведении множеств A и B содержится а*b элементов, т. е. n(A х B) = n(A) * n(В) = a * b. Например, если в множестве A содержится 3 элемента, в множестве B — 4 элемента, в множестве C — 5 элементов, то в их декартовом произведении будет содержаться 3 * 4* 5 = 60 упорядоченных наборов из трех элементов. 11. Объем и содержания понятия. Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Различают существенные и несущественные свойства объекта. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать (например, для квадрата существенными являются все вышеперечисленные свой- ства). Несущественно для квадрата ABCD свойство: «сторона AD горизонтальна». Объем понятия — это множество всех объектов, которые обобщаются в понятии и обозначаются одним термином. Любое понятие имеет не только объем, но и содержание. Содержание понятия — это множество всех существенных свойств объекта, отраженных в этом понятии. Рассмотрим, например, понятие «прямоугольник». Объем данного понятия — это множество различных прямо- угольников, а в его содержание входят такие свойства прямоугольника, как «иметь четыре прямых угла», «иметь равные противоположные стороны», «иметь равные диагонали». Между объемом понятия и его содержанием существует взаимосвязь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Например, объем понятия «квадрат» является частью объема понятия «прямоугольник», а содержание понятия «квадрат» включает в себя больше свойств, чем содержание понятия «прямоугольник». Если A является подмножествам B (A не равно B), то говорят, что понятие a — видовое по отношению к понятию b, а понятие b — родовое по отношению к понятию a. Например, если a — «прямоугольник», b — «четырехугольник», то их объемы A и B находятся в отношении включения, поскольку всякий прямоугольник является четырехугольником. Поэтому можно утверждать, что понятие «прямоугольник» — видовое по отношению к понятию «четырехугольник», а понятие «четырехугольник» — родовое по отношению к понятию «прямоугольник». Если A = B, то говорят, что понятия a и b тождественны. Например, тождественны понятия «равносторонний треугольник» и «равноугольный треугольник», так как их объемы совпадают. Рассмотрим подробнее отношение рода и вида между понятиями. Во-первых, понятия рода и вида относительны: одно и то же понятие может быть родовым по отношению к одному понятию и видовым по отношению к другому. Например, понятие «прямоугольник» — родовое по отношению к понятию «квадрат» и видовое по отношению к понятию «четырехугольник». Во-вторых, для данного понятия часто можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются понятия «четырехугольник», «параллелограмм», «многоугольник». В-третьих, видовое понятие обладает всеми свойствами родового понятия. Например, квадрат, являясь видовым понятием по отношению к понятию «прямоугольник», обладает всеми свойствами, присущими прямоугольнику. О понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и части: отрезок — часть прямой, а не ее вид. И если видовое понятие обладает всеми свойствами родового понятия, то часть не обязательно обладает всеми свойствами целого. Например, отрезок не обладает таким свойством прямой, как бесконечность. 12. Определение понятий. определение — это логическая операция, с помощью которой раскрывается содержание понятия либо устанавливается значение термина. По способу выявления содержания понятия различают явные и неявные определения. Среди явных определений в математике чаще всего используются определения через род и видовое отличие. В начальном курсе математики понятие «прямоугольник», как правило, определяют так: «Прямоугольником называется четырех- угольник, у которого все углы прямые». В этом определении есть две части — определяемое понятие (прямоугольник) и определяющее понятие (четырехугольник, у которого все углы прямые). Если обозначить через a первое понятие, а через b — второе, то данное определение можно представить в таком виде: a есть (по определению) b. Определения, имеющие такую структуру, называют явными. видовое отличие — это свойства (одно или несколько), которые позволяют выделять определяемые объекты из объема родового понятия. Формулируя определения понятий через род и видовое отличие, придерживаются ряда правил. Перечислим основные из них. Определение должно быть соразмерным. Это означает, что объемы определяемого и определяющего понятий должны совпадать. Данное правило вытекает из взаимозаменяемости, определяемого и определяющего понятий. Например, несоразмерно такое определение квадрата: «Ква- дратом называется четырехугольник, у которого все стороны рав- ны». Действительно, объем определяемого понятия — множество квадратов. Объем определяющего понятия — множество четырех- угольников, все стороны которых равны, а это множество ром- бов. Но не всякий ромб есть квадрат, т. е. объемы определяемого и определяющего понятия не совпадают, и, следовательно, данное определение несоразмерно. В определении (или их системе) не должно быть порочно- го круга. Это означает, что нельзя определять понятие через само себя (в определяющем не должно содержаться определяемого термина) или через другое, которое, в свою очередь, определяется через него. Например, содержит порочный круг определение: «Равные треугольники — это треугольники, которые равны». 3. Определение должно быть ясным. Например, нельзя определять прямоугольник как параллело- грамм с прямым углом, если понятие «параллелограмм» еще не рассмотрено. Одно и то же понятие определить через род и видовое отличие, соблюдая сформулированные правила, можно по-разному. Например, квадрат можно определить так: а) прямоугольник, у которого соседние стороны равны; б) прямоугольник, у которого диагонали взаимноперпендикулярны; в) ромб, у которого есть прямой угол; г) параллелограмм, у которого все стороны равны, а углы прямые. 13. Контекстуальные и остенсивные определения. При изучении математики в начальной школе чаще всего используют неявные определения. В неявных определениях содержание понятий раскрывается косвенным путем. Среди них различают контекстуальные и остенсивные.В контекстуальных определениях содержание нового понятия раскрывается либо через отрывок текста, либо через контекст, либо через анализ конкретной ситуации, описывающей смысл вводимого понятия. Примером контекстуального определения может быть определение уравнения и его решения, приведенное в учебнике математики для 2 класса. Остенсивные определения — это определения, раскрывающие существенные признаки предметов путем их предъявления, показа. Они используются для введения терминов путем демонстрации объектов, которые этими терминами обозначают. Например, таким способом можно определить в начальной школе понятия равенства и неравенства. В начальном обучении математике, кроме контекстуальных и остенсивных определений, часто используют приемы, заменя- ющие определение. Это, в частности, описание, сравнение. При описании изучаемого объекта ставится цель — выявить как можно больше его свойств, как существенных, так и несущественных. Если используется прием сравнения, то свойства вводимого понятия вы- являются в процессе сравнения различных объектов. Такой прием применяется, например, при ознакомлении младших школьников с понятием площади фигуры. 14. Высказывание и высказывательные формы. Высказыванием называют предложение, относительно которого имеет смысл вопрос: истинно оно или ложно. Например, предложения 1, 2, 4, 5 и 6, приведенные выше, есть высказывания, причем предложения 1, 4, 5 и 6 — истинные, а 2 — ложное. Высказывания принято обозначать прописными буквами латинского алфавита: A, B, C, …, Z. Если высказывание A истинно, то записывают: A — «и», если же высказывание A — ложно, то пишут: A — «л». «Истина» и «ложь» называются значениями истинности высказывания. Каждое высказывание либо истинно, либо ложно, быть одновременно тем и другим оно не может. Предложение x + 5 = 8 называют высказывательной формой. Оно порождает множество высказываний одной и той же формы. Итак, значение истинности элементарного высказывания определяют, исходя из его содержания с опорой на известные знания. Чтобы определить значение истинности составного высказывания, надо знать смысл логических связок, с помощью которых оно образовано из элементарных, и уметь выявлять логическую структуру высказывания. 15. Понятие разбиения множества на классы. Понятия множества и операций над множествами позволяют уточнить наше представление о классификации — действии распределения объектов по классам. Классификацию мы выполняем достаточно часто. Так, натуральные числа представляем как два класса: четные и нечетные. Углы на плоскости разбиваем на три класса: прямые, острые и тупые. Любая классификация связана с разбиением некоторого множества объектов на подмножества. При этом считают, что множество X разбито на классы X1, X2, …, Xn, …, если: подмножества X1, X2, …, Xn, … попарно не пересекаются; объединение подмножеств X1, X2, …, Xn, … совпадает с множеством X. Так как разбиение множества на классы связано с выделением его подмножеств, то классификацию можно выполнять с помощью свойств множества. 16. Число элементов в объедении и разности конечных множеств. Нам известно, как находят объединение двух конечных не- пересекающихся множеств. Например, если A = {x, y, z}, а B = {k, l, m, p}, то A  B = {x, y, z, k, l, m, p}. Чтобы ответить на вопрос: B = {x, y, z, k, l, m, p}. Чтобы ответить на вопрос: «Сколько элементов в полученном множестве?» — достаточно пересчитать их. А как определять число элементов в объединении конечных мно- жеств, не образуя его и не обращаясь к пересчету элементов? Условимся предложение «Множество A содержит a элементов» записывать в таком виде: n(A) = a. Например, если A = {x, y, z}, то утверждение «Множество A содержит три элемента» можно записать так: n(A) = 3. Можно доказать, что если в множестве A содержится a элемен- тов, а в множестве B — b элементов и множества A и B не пере- секаются, то в объединении множеств A и B содержится a b эле- ментов, т. е. n(A  B) = n(А) + n(В) = a * b. B) = n(А) + n(В) = a * b.
|





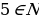 . Существуют множества конечные и бесконечные. Например: конечными является множество дней недели, месяцев в году, а бесконечными – множество точек на прямой. Для ряда числовых множеств в математике приняты стандартные обозначения: N — множество натуральных чисел; Z — множество целых чисел; Q — множество рациональных чисел;R — множество действительных чисел.
. Существуют множества конечные и бесконечные. Например: конечными является множество дней недели, месяцев в году, а бесконечными – множество точек на прямой. Для ряда числовых множеств в математике приняты стандартные обозначения: N — множество натуральных чисел; Z — множество целых чисел; Q — множество рациональных чисел;R — множество действительных чисел. B) \ C = (A \ C)
B) \ C = (A \ C)  C = (A
C = (A 









