| Этапы урока Цель этапа | Задания для учащихся, выполнение которых приведет к достижению планируемых результатов | Деятельность учителя | Деятельность учащихся | Формируемые УУД |
| 1.Организационный этап Цель: 1) включение учащихся в учебную деятельность, создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность. | Девиз урока: слушать и слышать, смотреть и видеть, думать и рассуждать. | Здравствуйте, ребята! Сегодня я хочу урок начать словами французского философа Ж. Ж. Руссо (1712-1778): “Вы талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошего умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…” | Включаются в деловой ритм урока.
| Метапредметные: коммуникативные планирование учебного сотрудничества с учителем и сверстниками. регулятивные организация своей учебной деятельности Личностные: мотивация учения |
| 2. Актуализация опорных знаний Цель: 1) организовать актуализацию изученных способов действий, достаточных для построения нового знания; 2) зафиксировать актуализированные способы действий в речи; 3) организовать актуализацию мыслительных операций, достаточных для построения нового знания: анализ, сравнение, обобщение.
| 1)Заполните пропуски: 1м=…см 1см= … м 1ц= … кг 1 кг=… ц 1руб=…коп. 1коп=…руб 2)С помощью листа бумаги показать наиболее часто используемые дроби. 3)Вычислите и сопоставьте ответы с буквами в таблице и составьте слово: 12,78*10= 127,8 14,52*100=1452 2,5*100=250 9,745:100=0,09745 0,0021*1000=2,1 0,74*100=74 843,5:10=84,35 3,08:0,01=308 0,0084:0,001=8,4 56,7*0,1=5,67
| -Давайте сравним полученные во всех заданиях ответы одинаковые.
-А какие дроби чаще всего встречаются в обычной жизни? Давайте проиллюстрируем это с помощью листа бумаги. - Назовите эти дроби. -1/100 тоже имеет свое название, а что бы его узнать выполним следующее задание.– правильный ответ на вопрос открывает.
-Одной я сотою зовусь, В расчетах вам всем пригожусь. Но лишь три буковки убрать, Могу я денежкою стать. -Какое слово мы получили? -Что же такое процент? -Сформулируйте тему и цель нашего урока. Запишем в тетрадь тему урока. Процент. Итак, в первом задании мы находили сотую часть числа. Значит 1%-это сотая часть числа. величины. | Участвуют в работе, отвечают на поставленные вопросы. Работают в парах -Во всех заданиях ответом является дробь - 1/100.
-Половина, четверть. -Работа в парах Игра «Математическое лото». Решают задачи, составляют слово. Должно получиться Пр..цент
-Процент -1/100 чего либо. | Предметные познавательные структурирование собственных знаний. Метапредметные коммуникативные организовывать и планировать учебное сотрудничество с учителем и сверстниками. регулятивные контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала. |
| 3. Постановка цели и задач урока. Мотивация учебной деятельности учащихся. Метод проблемной ситуации. Открытие новых знаний. Цель: Обеспечение мотивации учения детьми, принятия ими целей урока | Историческая справка Проценты –часто встречаются в повседневной жизни. Мы часто читаем или слышим, что в выборах приняли участие 52% избирателей, банк начисляет 12% годовых, молоко содержит 3,2% жира. Слово “процент” происходит от латинского слова pro centum, что буквально означает “со ста”. В клинописных табличках содержатся задачи на расчет процентов. Денежные расчеты с процентами были особенно распространены в Древнем Риме. Они называли процентами деньги, которые платил должник за каждую сотню. В средние века в Европе в связи с широким развитием торговли много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и для облегчения труда при вычисления процентов разрабатывали свои особые таблицы. Впервые опубликовал таблицы для расчета процентов в 1584 г. Симон Стевин – инженер из города Брюгге. Ныне процент – это частный вид десятичных дробей, сотая доля целого, принимаемого за единицу.
| -Давайте послушаем небольшую историческую справку о том, когда появилось слово процент. -Итак, в первом задании мы находили сотую часть числа, значит мы находили 1%. А как мы находили сотую часть числа? (делили на 100) Значит, записываем в тетрадь: 1% = 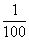 = 0,01 = 0,01 Обозначение: %. Вывод, чтобы проценты записать десятичной или обыкновенной дробью, нужно число, стоящее перед знаком процент, разделить на 100. -А как, вы думаете, как выполнить обратное преобразование, как десятичную или обыкновенную дробь записать в процентах? -Запомните равенства и запишите в тетрадь: 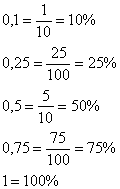
Проблемная ситуация Дан текст, прочитайте и с помощью него решите задачи Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика? Из 1800 га поля 558 га засажено картофелем. Какой процент поля засажен картофелем? Вопросы: Что такое проценты? Сколько процентов содержит вся величина? Как вычислить 1 % ? Как обратить проценты в десятичную дробь? Как обратить десятичную дробь в проценты? | Слушают сообщение о процентах, отвечают на вопросы.
-Делили на 100.
-умножить на 100.
| Предметные познавательные умение осознанно и произвольно строить речевое высказывание в устной форме, Развиваются умения ставить проблему, формулировать гипотезу, применять методы исследования (наблюдения, опыт, эксперимент, опрос, сравнение, анализ ит.д Личностные: самоопределение Метапредметные регулятивные целеполагание. коммуникативные умение вступать в диалог, участвовать в коллективном обсуждении вопроса. |
| 4. Применение знаний и умений в новой ситуации Цель: 1) уточнение темы урока; 2) определение средств (алгоритмы, модели, правила).
| Выполнение заданий: №№ 1062, 1064. -Разбор задачи 1 из учебника. Клубника содержит 6% сахара. Сколько килограммов сахара содержится в 15 кг клубники?
| Создание проблемной ситуации. Разбор задачи. -Что известно в задаче? -Что необходимо узнать? -Как найти 6% от 15 кг? -Можно ли сразу ответить на главный вопрос задачи? - Что необходимо сначала определить? -Что такое 1%? -Как найти 1 %? -Что мы находили в этой задаче? (6% от 15 кг, т.е. процент от числа.) Такие задачи называются задачами на нахождение процентов от числа. | Решают и записывают решения в тетради и на доске | Предметные познавательные: работа с информацией, использование знако-символических средств, общих схем решения Личностные: формирование готовности к самообразованию. Метапредметные коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других. регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. |
| Математическая зарядка (цель: проанализировать ошибки в домашней работе, настроить класс на активную работу) | 30%=0,3 50%=0,05 7%=0,07 325%=32,5% 7,6%=0,076 0,31=31% 2,6=26% 0,4=40%
| - Сейчас мы проведем математическую зарядку. Если вы, ребята согласны с утверждением, то поднимаете руки вперед, если нет, то – вверх. | Да нет да нет да да нет да
|
|
| 5. Контроль усвоения Цель: Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков | Выполняют самостоятельную работу, составляют слова, которые являются частью пословицы. Ученье - свет, а неученье тьма.
| Самостоятельная работа в парах. Тест
| Работают самостоятельно в тетради | Метапредметные регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. |
| 6. Подведение итогов урока Рефлексия Цель: Инициировать рефлексию детей по поводу психо-эмоционального состояния, мотивации, их собственной деятельности и взаимодействия с учителем и другими детьми в классе
| Анализируют свою работу на уроке. | + Я это знал | - Я этого не знал | ! Это меня удивило | ? Хотел бы узнать |
| Подошёл к концу наш урок. В этой пословице противопоставлены свет и тьма. Свет олицетворяет знания, полученные в результате учения, а тьма — невежество, культурную отсталость. Чтобы быть умным, образованным необходимость учиться. Давайте подведем итоги урока. Кто из вас выскажет мнение о пройденном уроке, вот фразы, с которых вы можете начать: | + Я это знал | - Я этого не знал | ! Это меня удивило | ? Хотел бы узнать | УРОК СЕГОДНЯ ЗАВЕРШЕН НО КАЖДЫЙ ДОЛЖЕН ЗНАТЬ: ПОЗНАНИЕ, УПОРСТВО, ТРУД К УСПЕХУ В ЖИЗНИ ПРИВЕДУТ! | Учащиеся отвечают на вопросы, анализируют свою работу, выражают вслух свои затруднения и обсуждают. правильность решения задач. Учащиеся оценивают себя и коллектив в целом | Метапредметные регулятивные: оценивание собственной деятельности на уроке Личностные: формирование позитивной самооценки
|
| 7.Домашнее задание Цель: Обеспечить понимание детьми содержания и способов выполнения домашнего задания |
| П. 37, №№1063, 1065. | Учащиеся записывают в дневники задание. |
|
| Самостоятельная работа. 1 вариант | Самостоятельная работа. 2 вариант | Самостоятельная работа. 1 вариант | Самостоятельная работа. 2 вариант |
| 1) 0,483 – это: р) 483% н) 4,83% у) 48,3% о) 0,483% | 1)Выразите 4% в виде десятичной дроби: н) 4 а)4 с)0,04 д)0,4 | 1) 0,483 – это: р) 483% н) 4,83% у) 48,3% о) 0,483% | 1)Выразите 4% в виде десятичной дроби: н) 4 а)4 с)0,04 д)0,4 |
| 2) 8% - это: ч) 0,08; г) 0,8; е) 0,008; м) 0,0008. | 2)Запишите дробь 1,26 в виде процентов: и)12,6% р)1,26% в) 126% ф)0,126% | 2) 8% - это: ч) 0,08; г) 0,8; е) 0,008; м) 0,0008. | 2)Запишите дробь 1,26 в виде процентов: и)12,6% р)1,26% в) 126% ф)0,126% |
| 3) 25% класса – это: и) половина учеников класса; а) пятая часть класса; е) четверть учеников класса; з) двадцать пятая часть класса | 3) Найдите 1% от 15: л) 1,5 м)150 т)15 е)0,15 | 3) 25% класса – это: и) половина учеников класса; а) пятая часть класса; е) четверть учеников класса; з) двадцать пятая часть класса | 3) Найдите 1% от 15: л) 1,5 м)150 т)15 е)0,15 |
| 4) Найдите 1% от 32: п)32 н)0,32 в) 3,2 у)0,032 | 4) Четверть в процентах -это: т) 25% р)40% б) 20% е)4% | 4) Найдите 1% от 32: п)32 н)0,32 в) 3,2 у)0,032 | 4) Четверть в процентах -это: т) 25% р)40% б) 20% е)4% |
| 5) Процент – это: ь) сотая часть числа, величины к) тысячная часть числа е)латинское слово | 5)20% класса- это: о) половина учеников класса; а) пятая часть класса; д) четверть учеников класса; з) двадцать пятая часть класса | 5) Процент – это: ь) сотая часть числа, величины к) тысячная часть числа е)латинское слово | 5)20% класса- это: о) половина учеников класса; а) пятая часть класса; д) четверть учеников класса; з) двадцать пятая часть класса |
| СЛОВО: | СЛОВО:
| СЛОВО: | СЛОВО: |
| 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= |
| 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= |
| 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= | 12,78*10= 14,52*100= 2,5*100= 9,745:100= 0,0021*1000= 0,74*100= 843,5:10= 3,08:0,01= 0,0084:0,001= 56,7*0,1= |
Проценты –часто встречаются в повседневной жизни. Мы часто читаем, что в выборах приняли участие 52% избирателей, банк начисляет 12% годовых, молоко содержит 3,2% жира.
Слово “процент” происходит от латинского слова pro centum, что буквально означает “со ста”. В клинописных табличках содержатся задачи на расчет процентов. Денежные расчеты с процентами были особенно распространены в Древнем Риме. Они называли процентами деньги, которые платил должник за каждую сотню. В средние века в Европе в связи с широким развитием торговли много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать проценты с процентов, т.е. сложные проценты, как называют их в наше время. Отдельные конторы и для облегчения труда при вычисления процентов разрабатывали свои особые таблицы. Впервые опубликовал таблицы для расчета процентов в 1584 г. Симон Стевин – инженер из города Брюгге. Ныне процент – это частный вид десятичных дробей, сотая доля целого, принимаемого за единицу.
Процент - сотая часть числа, величины. Обозначение: % 1% = = 0,01
Как проценты записать в виде дроби? Чтобы проценты нам в дробь обратить, надо число их на 100 разделить. 35%=35:100=0,35
Как дробь перевести в проценты. Дробь поскорее на 100 умножай, выраженье в процентах ее получай. 0,7=0,7 * 100%=70%
Проценты переводить в десятичную или обыкновенную дробь и наоборот. Решать задачи на нахождение дроби от числа.
Решать задачи на проценты.






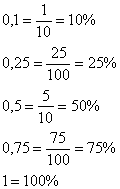
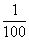 = 0,01
= 0,01 




















