Текстовые задачи, использующие уравнения в целых числах
Пример 3. Ваня и Петя ходили за грибами. Ваня нашёл 35 грибов, среди которых было несколько подосиновиков, а Петя грибов не нашёл. Ваня взял себе все белые грибы, а остальные отдал Пете. Петя, обнаружив среди них червивый подберёзовик, выкинул его. Сколько было найдено подосиновиков, если доля белых в найденных Ваней грибах оказалась равна доле подосиновиков в принесенных Петей домой грибах?
Решение. Обозначим число найденных Ваней подосиновиков за x , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
y35=x34-y, x,y∈N.
x=y(34-y)35.
Так как 35 = 5 ∙7 , а 5 и 7 – взаимно простые числа, то одно из чисел y
, а 5 и 7 – взаимно простые числа, то одно из чисел y и 34-y
и 34-y должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
Тогда x=20∙1435=4∙2=8. Таким образом, Ваня нашёл 8 подосиновиков.
Таким образом, Ваня нашёл 8 подосиновиков.
Ответ: 8 подосиновиков.
Пример 4. Любая из трёх барж разной грузоподъёмности может при полной загрузке в каждом рейсе перевезти некоторый груз, причём баржа наименьшей грузоподъёмности – за 15 рейсов. Две другие баржи перевозят весь груз за 3 совместных рейса. Сколько рейсов необходимо барже наибольшей грузоподъемности для перевозки всего груза, если недогрузка барж запрещается?
Решение. Пусть х и у – количество рейсов, за которое перевозят весь груз баржи баржи средней и наибольшей грузоподъёмности (x, y ∈N;15>x>y) , а объём (или масса) всего груза равен единице. Тогда 1x и 1y-
, а объём (или масса) всего груза равен единице. Тогда 1x и 1y-  грузоподъёмности этих двух барж.
грузоподъёмности этих двух барж.
По условию задачи баржи средней и наибольшей грузоподъёмности перевозят весь груз за 3 рейса. Тогда имеем уравнение:
31x+1y=1
1x+1y=13
1y=13-1x
1y=x-33x
y=3xx-3=3+9x-3.
Из последнего равенства следует, что число x-3 должно быть делителем числа 9. Если x-3=1,
должно быть делителем числа 9. Если x-3=1, то х = 4, у = 12; если x-3=3,
то х = 4, у = 12; если x-3=3, то х = 6, у = 6; если x-3=9,
то х = 6, у = 6; если x-3=9, то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
Ответ: 4 рейса.
Пример 5. Тринадцать пиратов делят клад золотых монет на палубе шхуны. При попытке разделить клад поровну оказалось, что остаётся 8 монет. Налетевшим штормом двух пиратов смыло за борт. Когда оставшиеся пираты снова стали поровну делить клад, то лишними оказались 3 золотые монеты. Затем в перестрелке погибли ещё три пирата. Когда уцелевшие пираты опять стали делить клад, то на этот раз оказалось, что остаётся 5 монет. Из какого количества монет состоял клад, если для его переноски достаточно сундука, вмещающего 500 золотых монет?
Решение. Пусть S ≤ 500 – количество монет, из которых состоит клад, k, m и n – число монет, которые достались бы каждому пирату при первом, втором и третьем делении соответственно. Согласно условиям задачи имеем следующую систему уравнений:
S=13k+8,S=11m+3,S=8n+5. 
Решим эту систему в целых числах. Рассмотрим сначала уравнение:
11m+3=8n+5
11m-8n=2
Найдем частное решение уравнения, им будет, например, m0 = 6, n0 = 8. Вычитая из равенства 11m-8n=2 равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11(m
равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11(m − 6) = 8(n
− 6) = 8(n − 8). Общее решение этого однородного уравнения в целых числах имеет вид: m
− 8). Общее решение этого однородного уравнения в целых числах имеет вид: m − 6 = 8l, n
− 6 = 8l, n − 8 = 11l, где l Î Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6, n
− 8 = 11l, где l Î Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6, n = 11l + 8, где l Î Z.
= 11l + 8, где l Î Z.
Следовательно, S=11m+3=118l+6+3=88l+66+3=88l+69 . Рассмотрим теперь уравнение 13k+8=88l+69 или 13k=88l+61.
. Рассмотрим теперь уравнение 13k+8=88l+69 или 13k=88l+61. Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
1. 13k=88l+61=13∙6+10l+61=78l+10l+61, 13k-78l=10l+61.
Левая часть последнего уравнения делится на 13. Следовательно, и правая часть должна делиться на 13, то есть 10l+61=13p, p∈  Z.
Z.
2. 10l=13p-61=10p+3p-61, 10l-10p=3p-61, 3p-61=10q, q ∈Z.
3. 3p=10q+61=3∙3+1q+61=9q+q+61, 3p-9q=q+61, q+61=3r, 
r∈Z, q=3r-61.
Вернёмся теперь к исходным переменным:
1. 3p=10q+61=103r-61+61=30r-610+61=30r-549, p=10r-183.
2. 10l=13p-61=1310r-183-61=130r-2379-61=130r-2440, 
l=13r-244.
3. S=88l+69=8813r-244+69=1144r-21472+69=1144r-21403
1144r-21403<500
1144r<500+21403
1144r<21903
r<219031144
r<191671144
При r=19 имеем S=1144∙19-21403=21736-21403=333, при
имеем S=1144∙19-21403=21736-21403=333, при  r=18
r=18 имеем S=1144∙18-21403=20592-21403=-811-
имеем S=1144∙18-21403=20592-21403=-811- не является натуральным числом. Значит, в кладе было 333 монеты.
не является натуральным числом. Значит, в кладе было 333 монеты.
Ответ: 333 монеты.
Просмотр содержимого документа
«Текстовые задачи, использующие уравнения в целых числах»
Текстовые задачи, использующие уравнения в целых числах
Пример 3. Ваня и Петя ходили за грибами. Ваня нашёл 35 грибов, среди которых было несколько подосиновиков, а Петя грибов не нашёл. Ваня взял себе все белые грибы, а остальные отдал Пете. Петя, обнаружив среди них червивый подберёзовик, выкинул его. Сколько было найдено подосиновиков, если доля белых в найденных Ваней грибах оказалась равна доле подосиновиков в принесенных Петей домой грибах?
Решение. Обозначим число найденных Ваней подосиновиков за 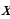 , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
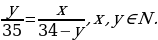
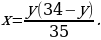
Так как 35 = 5 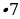 , а 5 и 7 – взаимно простые числа, то одно из чисел
, а 5 и 7 – взаимно простые числа, то одно из чисел 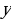 и
и 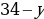 должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
Тогда 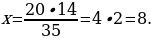 Таким образом, Ваня нашёл 8 подосиновиков.
Таким образом, Ваня нашёл 8 подосиновиков.
Ответ: 8 подосиновиков.
Пример 4. Любая из трёх барж разной грузоподъёмности может при полной загрузке в каждом рейсе перевезти некоторый груз, причём баржа наименьшей грузоподъёмности – за 15 рейсов. Две другие баржи перевозят весь груз за 3 совместных рейса. Сколько рейсов необходимо барже наибольшей грузоподъемности для перевозки всего груза, если недогрузка барж запрещается?
Решение. Пусть х и у – количество рейсов, за которое перевозят весь груз баржи баржи средней и наибольшей грузоподъёмности (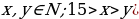 , а объём (или масса) всего груза равен единице. Тогда
, а объём (или масса) всего груза равен единице. Тогда 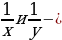 грузоподъёмности этих двух барж.
грузоподъёмности этих двух барж.
По условию задачи баржи средней и наибольшей грузоподъёмности перевозят весь груз за 3 рейса. Тогда имеем уравнение:
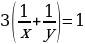
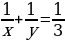
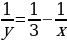
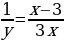
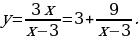
Из последнего равенства следует, что число 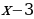 должно быть делителем числа 9. Если
должно быть делителем числа 9. Если 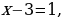 то х = 4, у = 12; если
то х = 4, у = 12; если 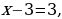 то х = 6, у = 6; если
то х = 6, у = 6; если 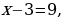 то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
Ответ: 4 рейса.
Пример 5. Тринадцать пиратов делят клад золотых монет на палубе шхуны. При попытке разделить клад поровну оказалось, что остаётся 8 монет. Налетевшим штормом двух пиратов смыло за борт. Когда оставшиеся пираты снова стали поровну делить клад, то лишними оказались 3 золотые монеты. Затем в перестрелке погибли ещё три пирата. Когда уцелевшие пираты опять стали делить клад, то на этот раз оказалось, что остаётся 5 монет. Из какого количества монет состоял клад, если для его переноски достаточно сундука, вмещающего 500 золотых монет?
Решение. Пусть S ≤ 500 – количество монет, из которых состоит клад, k, m и n – число монет, которые достались бы каждому пирату при первом, втором и третьем делении соответственно. Согласно условиям задачи имеем следующую систему уравнений:
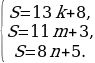
Решим эту систему в целых числах. Рассмотрим сначала уравнение:
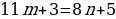
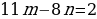
Найдем частное решение уравнения, им будет, например, m0 = 6, n0 = 8. Вычитая из равенства 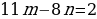 равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11(
равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11(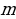 − 6) = 8(
− 6) = 8(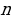 − 8). Общее решение этого однородного уравнения в целых числах имеет вид:
− 8). Общее решение этого однородного уравнения в целых числах имеет вид: 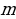 − 6 = 8l,
− 6 = 8l, 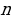 − 8 = 11l, где l Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6,
− 8 = 11l, где l Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6, 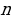 = 11l + 8, где l Z.
= 11l + 8, где l Z.
Следовательно, 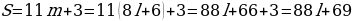 . Рассмотрим теперь уравнение
. Рассмотрим теперь уравнение 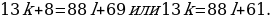 Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
1. 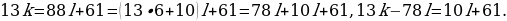
Левая часть последнего уравнения делится на 13. Следовательно, и правая часть должна делиться на 13, то есть 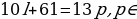 Z.
Z.
2. 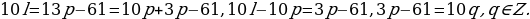
3. 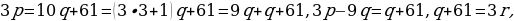
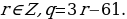
Вернёмся теперь к исходным переменным:
1. 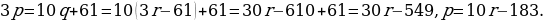
2. 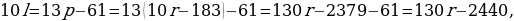
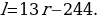
3. 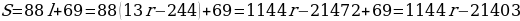
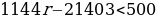
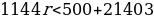
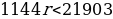
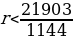
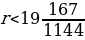
При 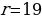 имеем
имеем 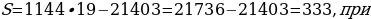
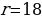 имеем
имеем 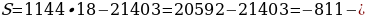 не является натуральным числом. Значит, в кладе было 333 монеты.
не является натуральным числом. Значит, в кладе было 333 монеты.
Ответ: 333 монеты.







 , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:

 , а 5 и 7 – взаимно простые числа, то одно из чисел y
, а 5 и 7 – взаимно простые числа, то одно из чисел y и 34-y
и 34-y должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20. Таким образом, Ваня нашёл 8 подосиновиков.
Таким образом, Ваня нашёл 8 подосиновиков. , а объём (или масса) всего груза равен единице. Тогда 1x и 1y-
, а объём (или масса) всего груза равен единице. Тогда 1x и 1y-  грузоподъёмности этих двух барж.
грузоподъёмности этих двух барж.




 должно быть делителем числа 9. Если x-3=1,
должно быть делителем числа 9. Если x-3=1, то х = 4, у = 12; если x-3=3,
то х = 4, у = 12; если x-3=3, то х = 6, у = 6; если x-3=9,
то х = 6, у = 6; если x-3=9, то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.


 − 6) = 8(n
− 6) = 8(n − 8). Общее решение этого однородного уравнения в целых числах имеет вид: m
− 8). Общее решение этого однородного уравнения в целых числах имеет вид: m . Рассмотрим теперь уравнение 13k+8=88l+69 или 13k=88l+61.
. Рассмотрим теперь уравнение 13k+8=88l+69 или 13k=88l+61. Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
 Z.
Z.











 имеем S=1144∙19-21403=21736-21403=333, при
имеем S=1144∙19-21403=21736-21403=333, при  r=18
r=18 имеем S=1144∙18-21403=20592-21403=-811-
имеем S=1144∙18-21403=20592-21403=-811- не является натуральным числом. Значит, в кладе было 333 монеты.
не является натуральным числом. Значит, в кладе было 333 монеты.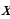 , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение: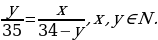
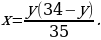
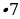 , а 5 и 7 – взаимно простые числа, то одно из чисел
, а 5 и 7 – взаимно простые числа, то одно из чисел 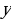 и
и 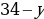 должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20. 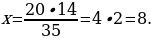 Таким образом, Ваня нашёл 8 подосиновиков.
Таким образом, Ваня нашёл 8 подосиновиков.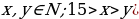 , а объём (или масса) всего груза равен единице. Тогда
, а объём (или масса) всего груза равен единице. Тогда 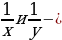 грузоподъёмности этих двух барж.
грузоподъёмности этих двух барж.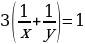
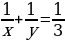
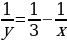
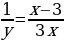
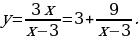
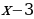 должно быть делителем числа 9. Если
должно быть делителем числа 9. Если 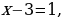 то х = 4, у = 12; если
то х = 4, у = 12; если 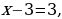 то х = 6, у = 6; если
то х = 6, у = 6; если 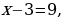 то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.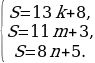
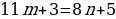
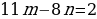
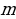 − 6) = 8(
− 6) = 8(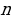 − 8). Общее решение этого однородного уравнения в целых числах имеет вид:
− 8). Общее решение этого однородного уравнения в целых числах имеет вид: 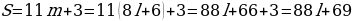 . Рассмотрим теперь уравнение
. Рассмотрим теперь уравнение 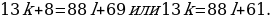 Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем: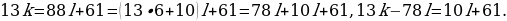
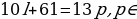 Z.
Z.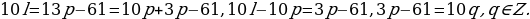
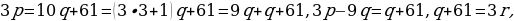
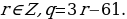
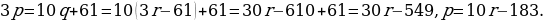
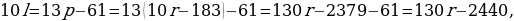
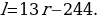
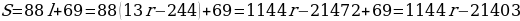
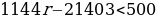
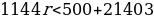
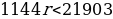
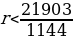
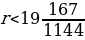
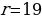 имеем
имеем 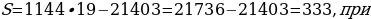
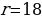 имеем
имеем 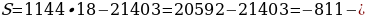 не является натуральным числом. Значит, в кладе было 333 монеты.
не является натуральным числом. Значит, в кладе было 333 монеты.









