Текстовые задачи, использующие уравнения в целых числах
Рассмотрим несколько текстовых задач, при решении которых возникают уравнения в целых числах. В таких задачах необходимым условием их решения является правильная формализация задачи, т.е. введение нужных переменных и составление уравнения (или системы уравнений), содержащего эти переменные.
Пример 1. Длина дороги, соединяющей пункты А и В, равна 2 км. По этой дороге курсируют два автобуса. Достигнув пункта А или пункта В, каждый из автобусов немедленно разворачивается и следует без остановок к другому пункту. Первый автобус движется со скоростью 51 км/час, а второй – 42 км/час. Сколько раз за 8 часов движения автобусы встретятся в пункте В, если известно, что первый стартует из пункта А, а второй – из пункта В?
Решение. Первый автобус проезжает путь между А и В за 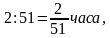 второй – за
второй – за  Если оба автобуса встретились в пункте В, то за одинаковое время первый проехал этот путь нечетное число раз, второй – четное число раз. Имеем:
Если оба автобуса встретились в пункте В, то за одинаковое время первый проехал этот путь нечетное число раз, второй – четное число раз. Имеем:



Из последнего уравнения видно, то  нечетно и кратно 7. Таких чисел в интервале от 1 до 84 шесть, это 7, 21, 35, 49, 63 и 77. Каждому такому
нечетно и кратно 7. Таких чисел в интервале от 1 до 84 шесть, это 7, 21, 35, 49, 63 и 77. Каждому такому  соответствует целое значение
соответствует целое значение 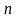 . Таким образом, за 8 часов движения автобусы встретятся в пункте В шесть раз.
. Таким образом, за 8 часов движения автобусы встретятся в пункте В шесть раз.
Ответ: 6 раз.
Пример 2. Мастер делает за 1 час целое число деталей, большее 5, а ученик – на 2 детали меньше. Один мастер выполняет заказ за целое число часов, а два ученика вместе – на 1 час быстрее. Из какого количества деталей состоит заказ?
Решение. Пусть x 5 деталей делает мастер за 1 час, тогда ученик за один час делает x – 2 детали. Пусть также мастер выполняет заказ за t часов, где t – целое число. Согласно условиям задачи имеем уравнение:
xt = 2(x – 2)(t – 1).




Дробь  должна быть целым числом. При x 5 это возможно, когда
должна быть целым числом. При x 5 это возможно, когда  или
или 
Если  , то
, то  , 6
, 6 детали в заказе.
детали в заказе.
Если  , то
, то  , 8
, 8 детали в заказе.
детали в заказе.
Ответ: из 24 деталей.
Пример 3. Ваня и Петя ходили за грибами. Ваня нашёл 35 грибов, среди которых было несколько подосиновиков, а Петя грибов не нашёл. Ваня взял себе все белые грибы, а остальные отдал Пете. Петя, обнаружив среди них червивый подберёзовик, выкинул его. Сколько было найдено подосиновиков, если доля белых в найденных Ваней грибах оказалась равна доле подосиновиков в принесенных Петей домой грибах?
Решение. Обозначим число найденных Ваней подосиновиков за  , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:

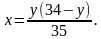
Так как 35 = 5  , а 5 и 7 – взаимно простые числа, то одно из чисел
, а 5 и 7 – взаимно простые числа, то одно из чисел  и
и  должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
должно делиться на 5, а другое – на 7. Перебирая все возможные варианты, получаем, что либо у = 20 и 34 – у = 14, либо у = 14 и 34 – у = 20.
Тогда Таким образом, Ваня нашёл 8 подосиновиков.
Ответ: 8 подосиновиков.
Пример 4. Любая из трёх барж разной грузоподъёмности может при полной загрузке в каждом рейсе перевезти некоторый груз, причём баржа наименьшей грузоподъёмности – за 15 рейсов. Две другие баржи перевозят весь груз за 3 совместных рейса. Сколько рейсов необходимо барже наибольшей грузоподъемности для перевозки всего груза, если недогрузка барж запрещается?
Решение. Пусть х и у – количество рейсов, за которое перевозят весь груз баржи баржи средней и наибольшей грузоподъёмности ( , а объём (или масса) всего груза равен единице. Тогда  грузоподъёмности этих двух барж.
грузоподъёмности этих двух барж.
По условию задачи баржи средней и наибольшей грузоподъёмности перевозят весь груз за 3 рейса. Тогда имеем уравнение:




Из последнего равенства следует, что число  должно быть делителем числа 9. Если
должно быть делителем числа 9. Если  то х = 4, у = 12; если
то х = 4, у = 12; если  то х = 6, у = 6; если
то х = 6, у = 6; если  то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
то х = 12, у = 4. Значит, решением уравнения служат пары (х, у) = {(12, 4); (6, 6); (4, 12)}, а решением задачи – пара х = 12, у = 4. Таким образом, баржа наибольшей грузоподъёмности сможет перевезти весь груз за 4 рейса.
Ответ: 4 рейса.
Пример 5. Тринадцать пиратов делят клад золотых монет на палубе шхуны. При попытке разделить клад поровну оказалось, что остаётся 8 монет. Налетевшим штормом двух пиратов смыло за борт. Когда оставшиеся пираты снова стали поровну делить клад, то лишними оказались 3 золотые монеты. Затем в перестрелке погибли ещё три пирата. Когда уцелевшие пираты опять стали делить клад, то на этот раз оказалось, что остаётся 5 монет. Из какого количества монет состоял клад, если для его переноски достаточно сундука, вмещающего 500 золотых монет?
Решение. Пусть S ≤ 500 – количество монет, из которых состоит клад, k, m и n – число монет, которые достались бы каждому пирату при первом, втором и третьем делении соответственно. Согласно условиям задачи имеем следующую систему уравнений:
Решим эту систему в целых числах. Рассмотрим сначала уравнение:


Найдем частное решение уравнения, им будет, например, m0 = 6, n0 = 8. Вычитая из равенства  равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11(
равенство 11·6 – 8·8 = 2, мы получим однородное уравнение: 11( − 6) = 8(
− 6) = 8(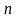 − 8). Общее решение этого однородного уравнения в целых числах имеет вид:
− 8). Общее решение этого однородного уравнения в целых числах имеет вид:  − 6 = 8l,
− 6 = 8l, 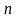 − 8 = 11l, где l Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6,
− 8 = 11l, где l Z. Соответственно, общее решение исходного уравнения в целых числах имеет вид: m = 8l + 6, 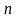 = 11l + 8, где l Z.
= 11l + 8, где l Z.
Следовательно, . Рассмотрим теперь уравнение Применим к этому уравнению алгоритм последовательного уменьшения модулей коэффициентов при неизвестных. Имеем:
1.
Левая часть последнего уравнения делится на 13. Следовательно, и правая часть должна делиться на 13, то есть Z.
2.
3.

Вернёмся теперь к исходным переменным:
1.
2.

3.



При  имеем
имеем  имеем не является натуральным числом. Значит, в кладе было 333 монеты.
имеем не является натуральным числом. Значит, в кладе было 333 монеты.
Ответ: 333 монеты.
Рассмотрим другой способ решения задачи: методом подбора.
Составим таблицу количества монет до 500 штук, при делении на 13 пиратов.
1 * 13 + 8 = 21,
2 * 13 + 8 = 34,
...
37 * 13 + 8 = 489.
Всего 37 вариантов.
Далее из всех вариантов оставим только те, деление которых на 11 даёт в остатке 3. Таких чисел всего три: 47, 190, 333.
Из них найдём число, которое имеет в остатке 5 при его делении на 8. Это число 333.
Ответ: клад состоял из 333 монет.
Пример 6. Абитуриенты сдавали экзамены в течение трёх дней в одних и тех же аудиториях первого корпуса. Число экзаменовавшихся каждый день абитуриентов в каждой аудитории было равно числу аудиторий. Если бы экзамены проводились во втором корпусе, то их можно было провести за два дня, используя каждый день одни и те же аудитории, причём каждый день в каждой аудитории абитуриентов удалось бы рассадить по рядам так, что число рядов, а также число людей в ряду было бы равным числу используемых аудиторий. Найти минимальное возможное число абитуриентов, которые могли бы быть проэкзаменованы при этих условиях.
Решение. Пусть х и у – количество аудиторий в первом и во втором корпусе соответственно. Согласно условиям задачи получаем уравнение
 .
.
Решим это уравнение в натуральных числах. Заметим сначала, что у должно делиться на 3, поэтому у = 3k, k N. Уравнение в этом случае принимает вид:



Выясним, при каких  число
число  является полным квадратом. Ясно, что это произойдёт тогда и только тогда, когда число 18k также будет полным квадратом. Имеем: 18k = n2, n N, откуда следует, что n2 делится нацело на 18, т.е. n = 6m, m N. Тогда
является полным квадратом. Ясно, что это произойдёт тогда и только тогда, когда число 18k также будет полным квадратом. Имеем: 18k = n2, n N, откуда следует, что n2 делится нацело на 18, т.е. n = 6m, m N. Тогда
18k = (6m)2, 18k = 36m2, 


Значит, Общее число абитуриентов в этом случае равно Таким образом, минимальное возможное число абитуриентов, которые могли бы быть проэкзаменованы при данных условиях, равно 432.
Ответ: 432 абитуриента.
Пример 7. Игорь и Володя решали задачу: некоторое заданное трёхзначное число прологарифмировать по основанию 2, из полученного числа вычесть некоторое заданное натуральное число и затем разность разделить на то же самое натуральное число. Игорь перепутал и в первом действии прологарифмировал по основанию 3, а Володя посчитал правильно. Когда они сверили свои результаты, оказалось, что полученные ими числа взаимно обратны. Найти исходное трёхзначное число.
Решение. Пусть х – заданное трёхзначное число, а у – заданное натуральное число. Согласно условию имеем следующее уравнение:
(
Откуда Заметим, что 62 = 36 – двузначное число, 63 = 216 – трёхзначное число, а 64 = 1296 – четырёхзначное число. Таким образом, условию задачи удовлетворяет х = 216 и у = 3.
Ответ: 216.
Задачи для самостоятельного решения
1. Учительница принесла в класс счётные палочки. Дети раскладывали их в пакетики. Когда разложили по две палочки в каждый пакетик, то осталась одна лишняя палочка. Затем разложили по 13 штук в пакетик, и тогда осталось 7 лишних палочек. Когда же палочки разложили по 9 штук в пакетик, то лишних не осталось. Сколько, самое меньшее, было счётных палочек? Ответ: 189 палочек.
2. Длина дороги, соединяющей пункты А и В, равна 3 км. По этой дороге курсируют два автобуса. Достигнув пункта А или пункта В, каждый из автобусов немедленно разворачивается и следует без остановок к другому пункту. Первый автобус движется со скоростью 50 км/час, а второй – 44 км/час. Сколько раз за 9 часов движения автобусы встретятся в пункте В, если известно, что первый стартует из пункта А, а второй – из пункта В?
3. Турфирма планирует экскурсионный маршрут для группы туристов с посещением городов А, В и С. Для проезда до города А по железной дороге были забронированы все места в 5 одинаковых вагонах и 1 место ещё в одном вагоне. Для проезда из А и В по морю были арендованы все места в 7 одинаковых яхтах и 2 места ещё в одной яхте. Для проезда из В в С были выкуплены все места в 11 одинаковых автобусах и 3 места ещё в одном автобусе. Определить количество туристов в группе, если на обратный путь заказан чартерный авиарейс на самолёт, вмещающий не более 400 пассажиров.
4. Один рабочий на новом станке производит за 1 ч целое число деталей, большее 8, а на старом станке – на 3 детали меньше. На новом станке один рабочий выполняет дневную норму за целое число часов, а два рабочих вместе выполняют норму на старых станках на 1 ч быстрее. Из какого количества деталей состоит дневная норма, если производительность рабочих одинакова?
5. Коля и Толя ходили за грибами. Толя нашёл 21 гриб, среди которых было несколько подберезовиков, а Коля грибов не нашёл. Толя взял себе все подосиновики, а остальные отдал Коле. Коля, обнаружив среди них червивый белый гриб, выкинул его. Сколько было найдено подберезовиков, если доля подосиновиков в найденных Толей грибах оказалась равна доле подберёзовиков в принесенных Колей домой грибах?
6. Любой из трёх грузовиков разной грузоподъемности при полной загрузке в каждой ездке может перевезти некоторый груз, причем грузовик с наименьшей грузоподъёмностью – за 10 ездок. Сколько совместных ездок необходимо двум другим грузовикам для перевозки всего груза, если недогрузка грузовиков запрещается?
7. Собранные на бахче арбузы уложили в одинаковые контейнеры, положив в каждый контейнер одинаковое число арбузов. Когда третью часть всех контейнеров погрузили в автомобили, то число погруженных контейнеров оказалось равно числу арбузов в одном контейнере. Пятая часть всех собранных арбузов была продана магазином в течение нескольких дней, причём каждый день продавалось одно и то же число арбузов, равное квадрату числа дней продажи. Какое минимальное количество арбузов могло быть собрано?
8. Саша и Олег решали задачу: некоторое заданное трёхзначное число прологарифмировать по основанию 3, полученное число разделить на некоторое заданное натуральное число, а затем из частного вычесть единицу. Саша перепутал и в первом действии прологарифмировал по основанию 5, а Олег посчитал правильно. Когда они сравнили свои результаты, оказалось, что полученные ими числа взаимно обратны. Найти исходное трёхзначное число.







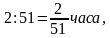 второй – за
второй – за  Если оба автобуса встретились в пункте В, то за одинаковое время первый проехал этот путь нечетное число раз, второй – четное число раз. Имеем:
Если оба автобуса встретились в пункте В, то за одинаковое время первый проехал этот путь нечетное число раз, второй – четное число раз. Имеем:


 нечетно и кратно 7. Таких чисел в интервале от 1 до 84 шесть, это 7, 21, 35, 49, 63 и 77. Каждому такому
нечетно и кратно 7. Таких чисел в интервале от 1 до 84 шесть, это 7, 21, 35, 49, 63 и 77. Каждому такому 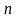 . Таким образом, за 8 часов движения автобусы встретятся в пункте В шесть раз.
. Таким образом, за 8 часов движения автобусы встретятся в пункте В шесть раз.



 должна быть целым числом. При x 5 это возможно, когда
должна быть целым числом. При x 5 это возможно, когда  или
или 
 , 6
, 6 детали в заказе.
детали в заказе. , то
, то  , 8
, 8 детали в заказе.
детали в заказе. , а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
, а белых грибов за y. Cогласно условиям задачи имеем следующее уравнение:
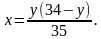
 , а 5 и 7 – взаимно простые числа, то одно из чисел
, а 5 и 7 – взаимно простые числа, то одно из чисел 









