Оглавление.
1.Введение. 2
1.1 Из истории математики. 3
1.2 Математические задачи. 4
2. Основная часть.
2.1 Методы решения задач.
1) Арифметический метод решения задач. 5
2) Алгебраический метод решения задач. 7
3) Комбинированный метод решения задач. 9
2.2 Текстовые задачи в заданиях ОГЭ.
1. Задачи на движение. 11
2. Задачи на движение по реке. 14
3. Задачи на работу. 15
4. Задачи на «концентрацию», на «смеси и сплавы» 16
5. Задачи на проценты. 18
3. Заключение.
1) Советы по организации деятельности учащихся при решении задач. 20
2) Выводы. 21
Литература 22
1. Введение.
Математика включает в себя очень много разделов – это и начальная математика, и алгебра, и геометрия, и тригонометрия, и математический анализ и т.д. Любой из этих разделов содержит текстовые задачи, которые в обучении математике занимают важное место: это и цель, и средство обучения. Умение решать задачи -показатель обучённости и развития учащихся. Научиться решать математические задачи очень важно, т. к., зная подходы к решению математических задач, учащиеся тем самым обучаются взаимодействию с любой задачей, которых достаточно много в других школьных предметах и в жизни вообще. Тем самым формируется жизненная позиция ученика как активной, самостоятельной личности. Текстовые задачи входят в ОГЭ и ЕГЭ, являются традиционным разделом на вступительных экзаменах в Вузы. Таким образом, данная тема имеет важнейшее значение в обучении математике, поэтому я и решил, что предметом моего исследования будут текстовые задачи.
Цели проекта:
1. Обобщение, углубление и систематизирование знаний по решению текстовых задач.
2. Демонстрация широты применения этой темы
3. Приобретение практических навыков при решении задач.
Задачи проекта:
1. Сформировать умения и навыки при решении разнообразных задач различной сложности.
2. Повысить уровень математической подготовки.
5. Подготовиться к успешной сдаче экзамена.
1.1 Из истории математики
"Математика (греч. matein - знание, наука) - наука о количественных отношениях и пространственных формах действительного мира. Первые понятия о математике появились в Древней Греции в 6-5 веках до нашей эры. Развитие математики до этого времени естественно отнести к периоду зарождения математических понятий, а 6-5 вв. до н. э. - время появления элементарной математики, продолжавшегося до 16 в. В течение этих двух первых периодов математические исследования стояли на очень ранних ступенях исторического развития в связи с самыми простыми потребностями хозяйственной жизни, сводившимися к счёту предметов, измерению площадей земельных участков, определению размеров отдельных частей архитектурных сооружений, измерению времени, коммерческим расчётам, навигации и т. п. Единственной наукой, зародившейся задолго до широкого развития математического изучения явлений природы в 17-18 вв. была астрономия, которая изрядно ускорила раннее развитие тригонометрии. Дальнейшее расширение круга аспектов, изучаемых математикой, привело в начале 19 в. к необходимости отнестись к процессу расширения предмета математических исследований более подробно и сознательно. Создание Н. И. Лобачевским его "воображаемой геометрии", получившей впоследствии вполне реальные применения, было первым значительным шагом в этом направлении. Развитие подобного рода исследований внесло в строение математики столь важные черты, и, следовательно, 19 и 20 вв. принято считать периодом современной математики." Итак подведём итог сказанному: счёт предметов на самых ранних ступенях развития культуры привёл к созданию простейших понятий арифметики натуральных чисел. Только на основе разработанной системы устного счисления возникают письменные системы счисления и постепенно вырабатываются приёмы выполнения над натуральными числами четырёх арифметических действий (сложение, вычитание, умножение и деление). Потребности измерения количества зерна, длины дороги и т. п. приводят к появлению названий и обозначений простейших дробных чисел и к разработке приёмов выполнения арифметических действий над дробями. Таким образом накапливался материал, складывающийся постепенно в древнейшую математическую науку — арифметику. Измерение площадей и объёмов, потребности строительной техники, существование астрономии, вызывают развитие геометрии. Эти процессы шли у многих народов в значительной мере независимо и параллельно. Особенное значение для дальнейшего развития науки имело накопление арифметических и геометрических знаний в Древнем Египте и Вавилоне. В Вавилоне на основе развитой техники арифметических вычислений появились также начала алгебры, а в связи с запросами астрономии - тригонометрия.
1.2 Математические задачи.
"Текстовые задачи в математике играют очень важную роль. Решая задачи, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления.
Все математические задачи появились из практического соображения. Ещё в далёком прошлом одним из стимулов изучения математики была потребность зарождающегося строительства и, возникшей вслед за ним, архитектуры. Остановимся на вопросе о классификации задач. Все текстовые математические задачи по числу действий, выполняемых для их решения, делятся на простые и составные. Задача, для решения которой надо выполнить один раз арифметическое действие, называется простой. Задача, для решения которой надо выполнить несколько действий, связанных между собой (независимо от того, будут ли это разные или одинаковые действия), называется составной. Простые задачи в системе обучения математике играют чрезвычайно важную роль. С помощью решения простых задач формируется одно из главных понятий начального курса математики – понятие об арифметических действиях. Умение решать простые задачи является подготовительной ступенью овладения учащимися умением решать составные задачи, так как решение составной задачи сводится к решению ряда простых задач. Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других. Решение составной задачи сводится к расчленению её на ряд простых задач и к последовательному их решению. Таким образом, для решения составной задачи надо установить систему связей между данными и искомым, в соответствии с которой выбрать, а затем выполнить арифметические действия.
2.Основная часть.
2.1 Методы решения текстовых задач.
Для решения текстовых задач применяются три основных метода: арифметический, алгебраический и комбинированный. Рассмотрим каждый из этих методов.
Арифметический метод.
Первым этапом решения задач арифметическим методом является разбор условия задачи и составление плана её решения. Этот этап решения задачи сопровождается максимальной мыслительной деятельностью.
Вторым этапом является решение задачи по составленному плану. Этот этап решения проводится учащимися без особых затруднений и в большинстве случаев носит тренировочный характер.
Третьим важным этапом решения задачи является проверка решения задачи. Она проводится по условию задачи. Пренебрежение проверкой при решении задачи, замена её проверкой ответов снижает роль решения задачи в процессе развития логического мышления учащихся.
При решении текстовых задач арифметическим методом у учащихся вырабатываются определённые умения и навыки, которые в процессе дальнейшего обучения должны совершенствоваться и закрепляться.
Умения и навыки, которые формируются в процессе решения задач только арифметическим методом, можно разбить на две группы. К первой группе относятся умения и навыки, которые необходимы для дальнейшего изучения математики. Все умения и навыки этой группы формируются в процессе решения задач на вычисление времени, т.е. тех задач, которые нет смысла решать алгебраически.
Вторая группа – это те умения и навыки, без знания которых можно решить все текстовые задачи алгебраическим методом, и в дальнейшем их незнание не будет пробелом в математическом образовании учащихся. Эти умения и навыки, несомненно, представляют интерес. Но почти все из них можно отнести к числу умений и навыков, формирующихся у учащихся при решении нестандартных задач. Решение таких задач следует проводить систематически наряду с решением стандартных текстовых задач.
Поют в хоре и занимаются танцами 82 студента, занимаются танцами и художественной гимнастикой 32 студента, а поют в хоре и занимаются художественной гимнастикой 78 студентов. Сколько студентов поют в хоре, занимаются танцами и художественной гимнастикой отдельно, если известно, что каждый студент занимается только чем-то одним?
Решение.
1-й способ.
1) 82  32 + 78 = 192 (чел.) - удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
32 + 78 = 192 (чел.) - удвоенное число студентов, поющих в хоре, занимающихся танцами и художественной гимнастикой;
2) 192: 2 = 96 (чел.) - поют в хоре, занимаются танцами и художественной гимнастикой;
3) 96 – 32 = 64 (чел.) - поют в хоре;
4) 96 – 78 = 18 (чел.) - занимаются танцами;
5) 96 – 82 = 14 (чел.) - занимаются художественной гимнастикой.
2-й способ.
1) 82 – 32 = 50 (чел.) - настолько больше студентов поют в хоре, чем
занимаются художественной гимнастикой;
2) 50 + 78 = 128 (чел.) - удвоенное число студентов, поющих в хоре;
3) 128: 2 = 64 (чел.) - поют в хоре;
4) 78 – 64 = 14 (чел.) — занимаются художественной гимнастикой;
5) 82 – 64 = 18 (чел.) - занимаются танцами.
Ответ: 64 студента поют в хоре, 14 студентов занимаются художественной гимнастикой, 18 студентов занимаются танцами.
Арбуз массой 20кг содержал 99% воды. Когда он немного усох, содержание воды в нем уменьшилось до 98%. Определите массу арбуза.
Для удобства решение будет сопровождаться иллюстрацией прямоугольников.
| 99% вода | 1% сухое вещество |
| 98% вода | 2% сухое вещество |
При этом желательно рисовать прямоугольники “сухого вещества” равными, потому что масса “сухого вещества” в арбузе остается неизменной.
1) 20:100=0,2 (кг) – масса “сухого вещества”;
2) 0,2:2=0,1 (кг) – приходится на 1% усохшего арбуза;
3) 0,1*100=10 (кг) – масса арбуза.
Алгебраический метод.
Под алгебраическим методом решения задач понимается такой метод решения, когда неизвестные величины находятся в результате решения уравнения или системы уравнений, решения неравенства или системы неравенств, составленных по условию задачи. Иногда алгебраическое решение задачи бывает очень сложным.
Пример 1. Рабочий может сделать определенное число деталей за три дня. Если он в день будет делать на 10 деталей больше, то справится с заданием за два дня. Какова первоначальная производительность рабочего и сколько деталей он должен сделать?
Решение.
1-й способ.
Пусть х д. в день - первоначальная производительность рабочего. Тогда (х + 10) д. в день - новая производительность, Зх д. – число деталей, которое он должен сделать. По условию получаем уравнение Зх = 2(х + 10), решив которое найдем х = 20. первоначальная производительность рабочего 20 деталей в день, он должен сделать 60 деталей.
2-й способ.
Пусть х д. – число деталей, которое должен сделать рабочий. Тогда  д. в день - новая производительность, (
д. в день - новая производительность, ( – 10) д. в день – первоначальная производительность рабочего по условию получаем уравнение х = 3(
– 10) д. в день – первоначальная производительность рабочего по условию получаем уравнение х = 3( – 10), решив которое найдем х = 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.
– 10), решив которое найдем х = 60. Рабочий должен сделать 60 деталей, его первоначальная производительность 20 деталей в день.
Ответ: 20 деталей в день; 60 деталей.
Пример 2. На солнышке грелось несколько кошек. У них вместе лап на 10 больше, чем ушей. Сколько кошек грелось на солнышке?
Решение.
1 способ.
Кошки х шт.
Лапы 4х шт.
Ушки 2х шт.
Так как лап на 10 больше чем ушей.
Составим и решим уравнение:
4х – 2х = 10
2х = 10 │: 2
х = 5
Ответ: 5 кошек грелось на солнышке.
2 способ.
На сколько лап больше чем ушей у одной кошки?
4 – 2 = 2 (шт.)
Сколько кошек грелось на солнышке?
10 : 2 = 5 (шт.)
Ответ: 5 кошек грелось на солнышке.
При решении задач алгебраическим методом основная мыслительная деятельность сосредотачивается на первом этапе решения задачи: на разборе условия задачи и составлении уравнений или неравенств по условию задачи.
Вторым этапом является решение составленного уравнения или системы уравнений, неравенства или системы неравенств.
Третьим важным этапом решения задач является проверка решения задачи, которая проводится по условию задачи.
В связи с внедрением в школьную программу элементов высшей математики, с ускоренным развитием и внедрением во все сферы вычислительной математики большое значение имеет формирование у учащихся не отдельных специфических навыков, а тех умений и навыков, которые имеют дальнейшее приложение. К числу этих умений и навыков относятся умения и навыки, которые формируются в процессе решения задач алгебраическим методом.
Комбинированный метод.
Иногда в ходе решения задачи применяются несколько методов: алгебраический и арифметический; геометрический, алгебраический и арифметический; арифметический и практический и т.п. Методы решения могут быть разными, но способ решения, лежащий в их основе, может быть один. Этот метод получается в результате включения в алгебраический метод решения задач решение, в котором часть неизвестных величин определяется с помощью решения уравнения или системы уравнений, неравенств или систем неравенств, а другая часть – арифметическим методом. В этом случае решение текстовых задач значительно упрощается.
Пример. Четыре товарища купили телевизор. Первый внес половину суммы, вносимой остальными, второй - треть того, что внесли все его товарищи, третий - четверть того, что все его товарищи, четвертый - оставшиеся 650 р. Сколько было уплачено за телевизор?
Решение:
Пусть первый товарищ внес х р., второй – у р., третий – z р. тогда, решая задачу чисто алгебраическим методом, по условию задачи получим достаточно громоздкую систему трех уравнений с тремя неизвестными.
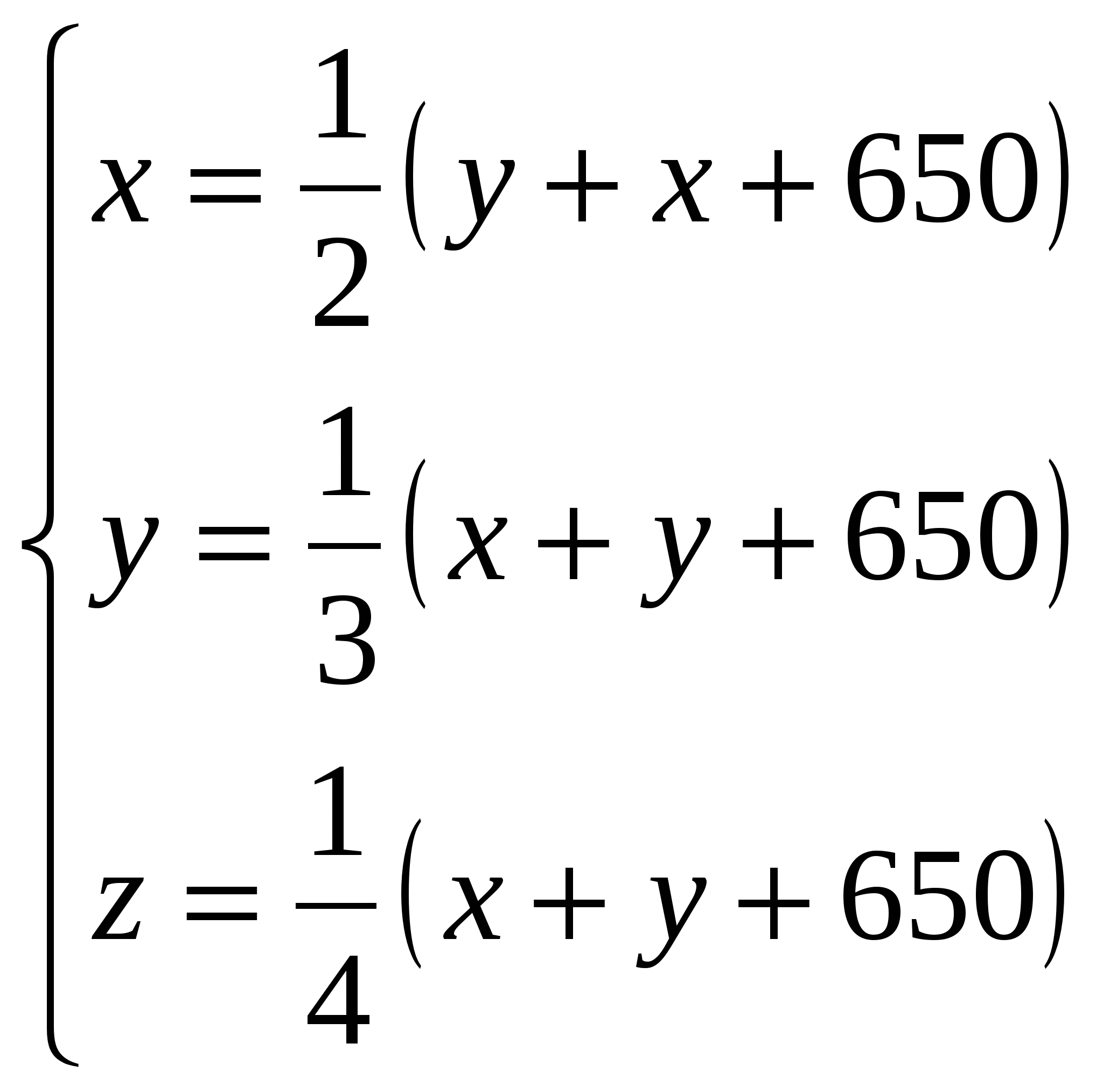
Решение начнем алгебраическим методом.
Пусть первый товарищ вне х р., тогда все остальные внесли 2х р. Отсюда находим стоимость телевизора: (р.). Значит, первый внес стоимости телевизора. Пусть второй внес у р., тогда все остальные внесли Зу р. Отсюда находим стоимость телевизора:
(р.). Значит, первый внес стоимости телевизора. Пусть второй внес у р., тогда все остальные внесли Зу р. Отсюда находим стоимость телевизора:  (р.). Значит, второй внес стоимости телевизора.
(р.). Значит, второй внес стоимости телевизора.
Пусть третий внес z р., тогда все остальные внесли 4z р. Отсюда находим стоимость телевизора:  (p.). Значит, третий внес стоимости телевизора.
(p.). Значит, третий внес стоимости телевизора.
Продолжим решение арифметическим методом.
Первый, второй и третий внесли  стоимости телевизора. Значит, четвертый внес остальные
стоимости телевизора. Значит, четвертый внес остальные  стоимости. По условию это составляет 650 р. Следовательно, телевизор стоит
стоимости. По условию это составляет 650 р. Следовательно, телевизор стоит р.
р.
Ответ: 3 000 р.
2.2 Текстовые задачи в заданиях ОГЭ.
1. Задачи на движение. 
Задачи на движение, как правило представляют собой задачи с использованием объектов, совершающих какое-либо действие. Это могут быть пешеходы, велосипедисты, автомобили, лодки и так далее. Существует 3 вида задач на движение: движение двух объектов навстречу друг другу, движение в противоположных и обратных направлениях, движение из одной точки в одном направлении. Доминирующими понятиями в таких задачах являются скорость(V), время(t) и расстояние(S) и формула, связывающая эти понятия:
S = V * t. Для начала разберём простые задачи, решающиеся в одно действие, для того чтобы закрепить эти понятия. Рассмотрим задачу: "Расстояние от города до поселка 30 км. Сколько времени потребуется пешеходу, чтобы пройти это расстояние со скоростью 6 км/ч?" Эта задача требует изначальные понятия арифметики, такие как деление, и решается в одно действие. Подставив формулу t=S/v получим: 30км / 6км/ч = 5ч. В итоге записываем ответ: Пешеходу потребуется 5 часов. В данной задаче мы находили время. Рассмотрим ещё одну простую задачу нахождения скорости пешехода: "От деревни Ивантеева до села Воронова 20 км. Миша был в пути 4 часа. С какой скоростью перемещался Миша?" Данная задача также простая и решается при подстановке формулы V=S/t: 20 км / 4ч =5км/ч. Миша перемещался со скоростью 5км/ч.
Перейдём к решению составных задач, и для начала рассмотрим задачи движения двух объектов навстречу друг другу: «От пункта А до пункта B 36 км. Первый пешеход вышел из пункта А со скоростью 5 км/ч а второй пешеход из пункта B со скоростью 4 км/ч. Через сколько времени они встретятся?» В этой задаче уже нужно представить картинку и проанализировать свои дальнейшие действия. Первым действием мы находим суммарную скорость пешеходов: 4 км/ч + 5 км/ч = 9 км/ч. Вторым действием мы находим время, формулу времени выражаем из формулы нахождения расстояния: t = S / V. Получаем: 36 км / 9 км/ч = 4 часа. И в итоге записываем ответ: Пешеходы встретятся через 4 часа.
Данные задачи были простые, так как не было введено осложняющих условий, таких как: разное время старта движения объектов; изменение скорости на различных участках пути; задержка на различных участках пути.
Велосипедист подсчитал, что если он поедет со скоростью 6 км/ч, опоздает на 1 час, если поедет со скоростью 9 км/ч, то приедет на 1 час раньше намеченного срока. С какой скоростью нужно ехать велосипедисту, чтобы приехать вовремя?
Рассмотрим задачу
Сначала рассмотрим арифметическое решение.
Допустим, что выехали два велосипедиста, у первого скорость 6 км/ч, а у второго – 9 км/ч. Тогда:
1). 6.1= 6 (км) – столько километров не доедет до намеченного места первый велосипедист при скорости 6 км/ч
2). 9.1= 9 (км) – столько лишних километров проедет второй велосипедист при скорости 6 км/ч
3). 6+9= 15 (км) – расстояние между велосипедистами в назначенное время
4). 9 – 6 = 3 (км/ч) – скорость удаления первого велосипедиста от второго
5). 15:3 = 5 (ч) - время удаления
6). 6. (5+1) = 36 (км) – расстояние до места назначения
7). 36: 5 = 7,2 (км/ч) – необходимая скорость
Ответ: велосипедисту необходимо ехать со скоростью 7,2 км/ч
Теперь рассмотрим решение этой же задачи с помощью уравнения:


 9км/ч 1ч
9км/ч 1ч



 6 км/ч 1ч
6 км/ч 1ч
Пусть х ч – намеченное время движения, тогда путь при скорости 6 км/ч равен 6(х+1) км или при скорости 9 км/ч равен 9(х – 1) км. Составим уравнение:
6(х+1) = 9(х – 1)
х = 5
При х = 5 необходимая скорость будет равна 6(5+1):5 = 7,2 (км/ч)
Ответ: велосипедисту необходимо ехать со скоростью 7,2 км/ч
Как видим, арифметическое решение потребовало большей изобретательности. Использование уравнения как математической модели преобразования жизненной ситуации позволяет упростить процесс решения задачи.
Задачи на движение по реке.
Пример 1. Катер проходит некоторое расстояние по озеру за 6 ч, по течению реки за 5 ч. Сколько времени потребуется плоту, чтобы пройти такое же расстояние по течению реки?












5 ч Vк +Vр
6 ч Vк

? ч Vр = Vп
Решение: Пусть х км – данное расстояние, тогда  км/ч – скорость катера по течению,
км/ч – скорость катера по течению,  км/ч скорость катера в стоячей воде. – скорость течения,
км/ч скорость катера в стоячей воде. – скорость течения,  - потребуется плоту на такое расстояние.
- потребуется плоту на такое расстояние.
Пример 2.
Теплоход от Киева до Херсона идет трое суток, а от Херсона до Киева - 4 суток (без остановок). Сколько времени от Киева до Херсона будут плыть плоты?

Vст +Vр, 3 суток







Vст – Vр, 4 суток
Киев Херсон


Vп = Vр? суток
Решение: пусть расстояние от Киева до Херсона х км, тогда скорость теплохода по течению Vст +Vр = км/сут, против течения Vст –Vр =
км/сут, против течения Vст –Vр = км/сут, где Vст – собственная скорость теплохода и Vр – скорость реки
км/сут, где Vст – собственная скорость теплохода и Vр – скорость реки
1). удвоенная скорость течения
2). - скорость течения
3). - время движения плотов
Ответ: 24 дня.
3. Задачи на работу.
А = рt, из этой формулы легко найти р (производительность) или t.
Если объем работы не важен и нет никаких данных, позволяющих его найти – работу принимаем за единицу.
Если трудятся два рабочих (два экскаватора и т.д.) – их производительности складываются.
В качестве переменной удобно взять производительность.
Пример 1.
Две машинистки вместе могут перепечатать рукопись за 6 часов. После 5 часов совместной работы вторая машинистка продолжила работу самостоятельно и завершила ее за 3 часа. За какое время каждая машинистка смогла бы перепечатать рукопись?
Примем объем работы за 1. Пусть первая машинистка сможет перепечатать рукопись за х часов (х0), вторая машинистка – за у часов (у0), 1/х – производительность первой машинистки, а 1/у – производительность второй. По условию задачи, работая вместе, они могут перепечатать рукопись за 6 часов; 6(1/х+ 1/у) =1. Если машинистки будут работать вместе 5 часов, то они напечатают 5(1/х+ 1/у) часть работы, а если вторая машинистка будет работать 3 часа, она напечатает 3/у части работы. По условию задачи работа при этом будет завершена 5(1/х+ 1/у) +3/у=1. Учитывая, что х0, у0, составим и решим систему уравнений:
6(1/х+ 1/у) =1, х=9,
5(1/х+ 1/у) +3/у=1; у=18.
Ответ: первая машинистка может перепечатать рукопись за 9 часов,
а вторая – за 18 часов.
Пример 2.
Двое рабочих, работая вместе, могут оклеить комнату обоями за 6 часов. За сколько часов может оклеить комнату каждый из них в отдельности, если первый это сделает на 5 часов быстрее второго?
Пусть первый рабочий может наклеить обои в комнате за х часов (х0), тогда второй рабочий наклеит обои за (х+5) часов. Всю работу примем за 1, тогда 1/х – производительность первого рабочего, 1/(х+5) – производительность второго. Так как, работая вместе, они наклеят обои за 6 ч, то их совместная производительность равна 1/6. Таким образом, имеем
1/х + 1/(х+5) = 1/6
х²-7х-30=0
х₁=10, х₂=-3 не удовлетворяет условию х0, т.е. х=10.
Таким образом, первый рабочий может выполнить работу за 10 ч,
а второй – за 15 ч.
Ответ: первый рабочий может выполнить работу за 10 ч,
а второй – за 15 ч.
4.Задачи на «концентрацию», на «смеси и сплавы»
В задачах этого типа обычно присутствуют три величины, соотношение между которыми позволяет составлять уравнение:
Концентрация (доля чистого вещества в смеси);
Количество чистого вещества в смеси (или сплаве);
Масса смеси (сплава).
Соотношение между этими величинами следующее:
Масса смеси • концентрация = количество чистого вещества
Пример 1.
Сплав меди с цинком, содержащий 5 кг цинка, сплавлен с 15 кг цинка. В результате содержание меди в сплаве понизилось по сравнению с первоначальным на 30%. Какой могла быть первоначальная масса сплава?
РЕШЕНИЕ:
Пусть х кг – масса меди в сплаве,
тогда (х+5) кг – первоначальная масса сплава;
(х/(х+5))∙100% - процентное содержание меди в первоначальном сплаве; (х+5+15)кг – масса нового сплава;
( х/(х+5+15))∙100% - процентное содержание меди в новом сплаве.
По условию содержание меди понизилось на 30%. Составим и решим уравнение:
(х/(х+5))∙100-( х/(х+5+15)) ∙100=30, х 0
10х²+200х-10х²-50х=3(х+5)(х+20)
150х=3(х+5)(х+20)
50х=(х+5)(х+20)
х²+25х-50х+100=0
х²-25х+100=0
х₁=5, х₂=20. Оба числа удовлетворяют условию х 0.
Ответ: первоначальная масса сплава могла быть либо 10 кг, либо 25 кг.
Пример 2.
Смешали 30%-ный и 50%-ный растворы азотной кислоты и получили 45%-ный раствор. Найдите отношение массы 30%-го раствора к массе 50%-го раствора.
Пусть х г – масса первого раствора, у г – масса второго раствора, тогда 0,3х г – масса кислоты в первом растворе, 0,5у г – масса кислоты во втором растворе,
(0,3х+0,5у) г – масса кислоты в смеси, что по условию задачи составляет 45% массы раствора. Составим уравнение:
0,3х+0,5у=0,45(х+у)
0,5у-0,45у=0,45х-0,3х
0,05у=0,15х
у=3х
х: у=1:3
Ответ: отношение массы 30%-го раствора к массе 50%-го раствора как 1:3.
Задачи на проценты.
Решение задач на проценты сводится к основным трем действиям с процентами:
-нахождение процентов от числа;
-нахождение числа по его процентам;
-нахождение процентного отношения чисел.
Пример 1.
Покрасив 2 метра забора, Том Сойер «уступил» это занятие другому мальчику, который покрасил 30% неокрашенной части забора. После этого Том трижды «уступал «своё право красить забор другим мальчикам. Первый и второй из них покрасили соответственно 1/5 и 1/6 всего забора, а третий - 85% оставшейся неокрашенной части забора. Какова длина забора, если последний оставшийся метр Том красил сам?
РЕШЕНИЕ:
Пусть х-длина всего забора, тогда 0,3(х-2) – длина части забора, которую покрасил мальчик, красивший сразу за Томом, а из следующих трех мальчиков первый и второй покрасили ⅕∙х и ⅙∙х метров. Пусть у – длина части забора, оставшейся неокрашенной после этого. Из условия следует, что 1 метр (который в конце красил Том) составляет 100% - 85% = 15% от у.
То есть 0,15у=1, у=100/15=20/3. Так как сумма всех покрашенных частей равна длине всего забора, получаем уравнение:
2+ 0,3(х-2) + ⅕∙х + ⅙∙х +у=х
2+0,3х-0,6+11/30∙х+20/3=х
20/30∙х+1,4+20/3=х
х=24,2(м)
Ответ: длина забора 24,2 метра.
Пример 2.
Находясь в гостях у Кролика, Винни-Пух за первые три часа съел 40% всего запаса меда Кролика. Пятачок и Кролик вместе за это же время съели 300 граммов меда. За следующие три часа Винни-Пух съел 2/3 оставшегося меда, а Пятачок и Кролик съели 100 граммов меда на двоих, после чего у Кролика осталось 1,6 кг меда. Сколько меда было у Кролика до визита Винни-Пуха?
РЕШЕНИЕ:
Пусть первоначально у кролика было х кг меда. Винни-Пух за первые 3 часа съел 0,4х кг, а Пятачок и кролик съели 300г меда. У кролика осталось х-0,4х-0,3=0,6х-0,3(кг).
За следующие 3 часа Винни-Пух съел 2/3(0,6х-0,3)=0,4х-0,2(кг),
а Пятачок и кролик – 100г. У кролика осталось
0,6х-0,3-0,4х+0,2-0,1=0,2х-0,2(кг)
Зная, что осталось 1,6 кг, составим уравнение:
0,2х-0,2=1,6
х=9(кг)
Ответ: первоначально у кролика было 9 кг меда.
3. Заключение.
При решении текстовых задач учащимся могут помочь несколько простых и общих советов.
Совет 1. Не просто прочитайте, а тщательно изучите условие задачи. Попытайтесь полученную информацию представить в другом виде – это может быть рисунок, таблица или просто краткая запись условия задачи.
Совет 2. Выбор неизвестных.
В задачах "на движение" – это обычно скорость, время, путь. В задачах “на работу” - производительность и т.д.
Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и можно было составить соответствующую “математическую модель” (уравнение, неравенство, система уравнений или неравенств).
Совет 3. Составление и решение “математической модели”.
При составлении “математической модели” (уравнения, неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи. Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи и чему в тексте задачи соответствует каждый “знак” полученной записи (сами неизвестные, действия над ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить составленное.
Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и полученную запись).
Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации. Например, не x и y, а x+y, x/y, 1/x и т.п.
Если кажется, что получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.
Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.
Совет 4. Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.
При решении задач короткую запись задачи можно сделать с помощью рисунка или таблицы.
Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.
Можно выделить семь вопросов, которые дают верное направление решению задач разных типов.
Вопросы к задаче с комментариями к ним:
О каком процессе идёт речь? Какими величинами характеризуется этот процесс? (Количество величин соответствует числу столбцов таблицы).
Сколько процессов в задаче? (Количество процессов соответствует числу строк в таблице).
Какие величины известны? Что надо найти? (Таблица заполняется данными задачи).
Как связаны величины в задаче? (Вписать основные формулы, выяснить связи и соотношения величин в таблице).
Какую величину (величины) удобно выбрать в качестве неизвестной или неизвестных? (Клетки в таблице заполняются в соответствии с выбранными неизвестными).
Какие условия используются для составления «модели»? (Выписать полученную «модель»)
Легко ли решить полученное? (Если решить сложно, ввести новые переменные, использовать другие соотношения)
Выводы:
Для того, чтобы научиться решать задачи, надо приобрести опыт их решения путем многократного повторения операций, действий, составляющих предмет изучения.
Редкие ученики самостоятельно приобретают такой опыт. Долг учителя - помочь учащимся приобрести опыт решения задач, научить их решать задачи.
Помощь учителя не должна быть чрезмерной, но и не быть слишком малой.
Навыки решения текстовых задач формируются на основе осмысленных знаний и умений.
Для формирования навыков нужна тщательно продуманная система упражнений и задач «от простого к сложному».
Знания учащихся по математике должны совершенствоваться с решением каждой новой задачи.
Следует учитывать индивидуальные особенности и возможности учащихся.
Приоритетными формами являются учебные занятия, предполагающие активную самостоятельную познавательную деятельность обучающихся, работа в группах, парах, взаимообучение.
Планируемые результаты: По завершении проекта обучающиеся смогут решать текстовые задачи различной сложности.
Проверить успешность проекта можно путем проведения проверочной работы.
Литература
1.Бизам, Д. Игра и логика. 85 логических задач //Д. Бизам, Я. Герцег.– М.: Мир, 1975.– 358 с. : ил.
2.Математика: Учебник для 5 класса общеобразовательных учреждений// А.Г. Мерзляк.–Вентана-Граф, 2017-304 с..
3.Математика: Учебник для 6 класса общеобразовательных учреждений// А.Г. Мерзляк.–Вентана-Граф, 2017-304 с.
4.Кочагин В.В. Математика // Тематические тренировочные задания/ В. В. 5.Кочагин, М. Н. Кочагина. – М.: Просвещение, 2008.
6.Ресурсы Интернет: http: //www.eidos.ru/journal/2002/0920.htm
7.Ресурсы Интернет: http://www.erudition.ru
8.Ресурсы Интернет: http:// docs.google.com
9.Ресурсы Интернет: http://ipk.admin.tstu.ru/sputnik
22






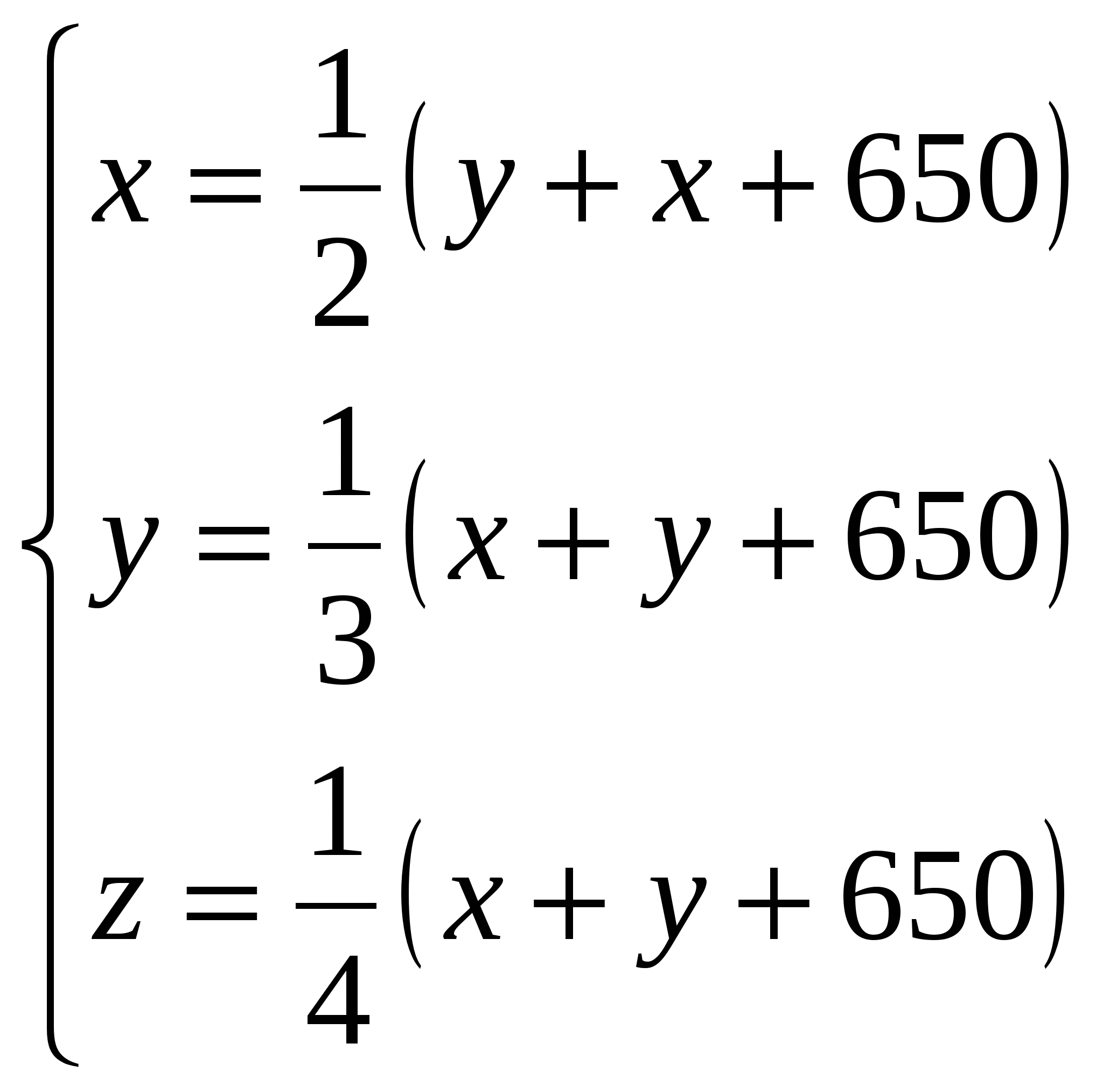



 9км/ч 1ч
9км/ч 1ч


 6 км/ч 1ч
6 км/ч 1ч























