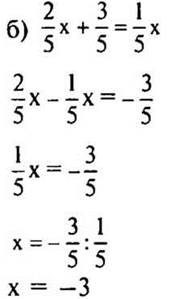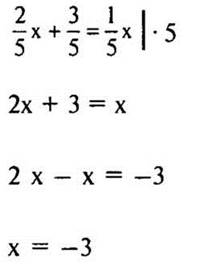Тема урока: « Перпендикулярные прямые».

Тема урока: « Перпендикулярные прямые».

Тип урока: урок получения новых знаний.

Класс: 6 класс.

Цели урока: ввести понятие и обозначение перпендикулярных прямых, перпендикулярных отрезков и лучей; показать способы построения перпендикулярных прямых; отрабатывать умение строить перпендикулярные прямые; развивать наблюдательность, а также коммуникативные умения, воспитывать аккуратность, внимательность, усидчивость.

Ход урока

I. Организационный момент

II. Анализ контрольной работы

1. Познакомить учащихся с результатами контрольной работы.

2. Выполнить работу над ошибками, решив задания, в которых допущено наибольшее количество ошибок, задания, вызвавшие затруднения у учащихся.

III. Устный счет

1 .Упростите выраженя:

12m + 16 + 2m + m;

2 * 5z + 5z.

1. Решите уравнения:

8 + 31у = 32у (у = 8);

6 - 8х = 7 - 9х (х = 1);

2у + 4 = -9 + 3у (у = 13).

2. За кусок пицы и салат «Цезарь» вы заплатили 200 рублей. Салат дороже пиццы в 3 раза. Сколько стоит пицца? (50 руб.)

3. Какую часть метра составляет 250 миллиметров?

4. Какую часть часа составляют 10 минут?

IV. Индивидуальная работа ( 1 вариант составлен для менее подготовленных учащихся, первые выполнившие 3 номера, выполняют 4 задание на обратной стороне поворотной доски доски )

1 карточка

1. Раскрыть скобки и найти значение выражения:

4,23 - (3,24 + 8,4) - 4,23 + 3,24. (-8,4)

2. Решить уравнение: 2(7х — 4) — 2(2х — 3) = 12. ( 2 )

3. Привести подобные слагаемые: 12а - 17b + 13b - 12а + 2а.

4. Упростить выражение: -3(2а + 5с) - 2(-5а - 6с). (4а -3с)

2 карточка

1. Раскрыть скобки и найти значение выражения:

4,49 - (6,21 + 3,3) + (6,7 - 4,49) + 6,21.

2. Решить уравнение: —7(3х — 8) + 3(4х + 5) = 8.

3. Привести подобные слагаемые: 23m — 21n + 16n — 13m — 16n.

4. Упростить выражение: —2(3а + 6с) + 8(с — а) —3(—6а — 7с).

V. Сообщение темы урока

— Сегодня для работы на уроке нам понадобится транспортир и чертежный треугольник. А вот зачем, вы узнаете в течение урока.

VI. Изучение нового материала

1. Подготовительная работа.

— Вспомним что мы знаем о прямой ( используем слайд)

— Какие виды углов вы знаете? (Слайд.Прямой, острый, тупой, развернутый.)

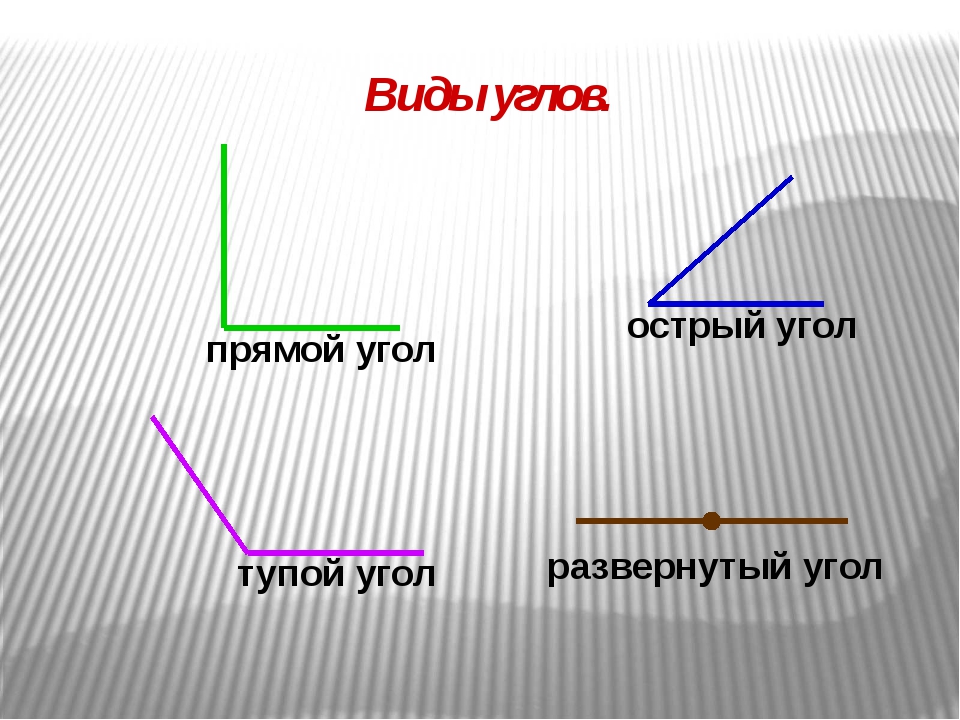
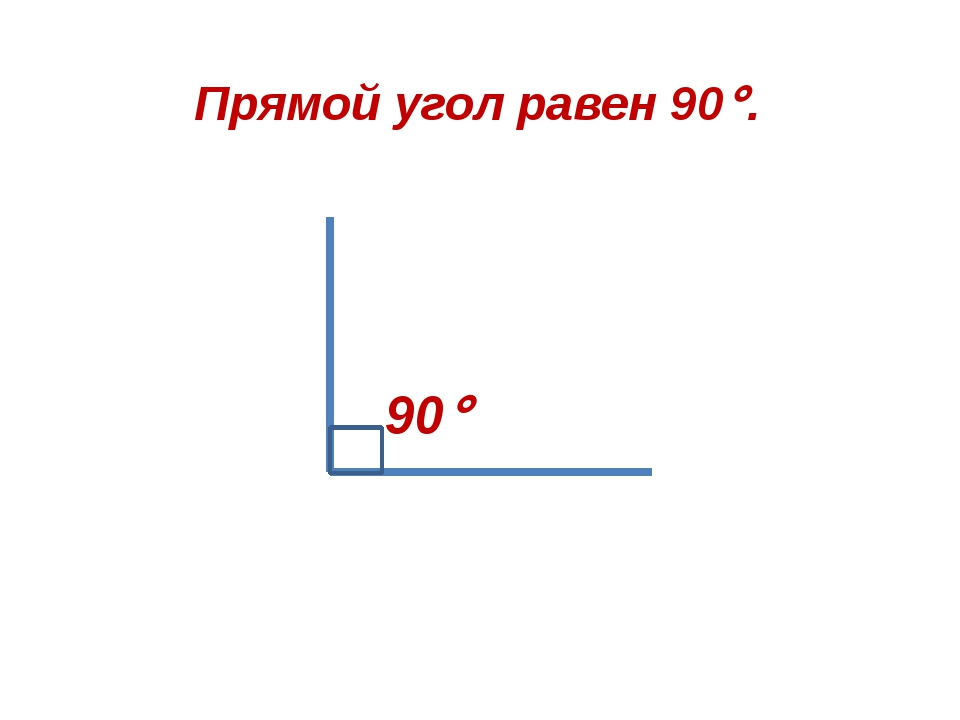
— Дайте определение прямого угла. (Слайд.Угол, градусная мера которого равна 90°, называется прямым углом.)

— Как называется прибор для измерения углов? (Транспортир.)

2. Работа над новой темой.

— Постройте две пересекающиеся прямые.

— Обозначьте их.

— Сколько углов получилось при пересечении этих прямых? (6)

— Что у всех углов общего? (Общая вершина — точка пересечения прямых.)

— Что можете сказать о парах этих углов? (Они равны.)

(Показать на чертеже.)

— Если все четыре угла равны между собой, то каждый угол равен 90°.

Определение. Две прямые, образующие при пересечении прямые углы, называют перпендикулярными.

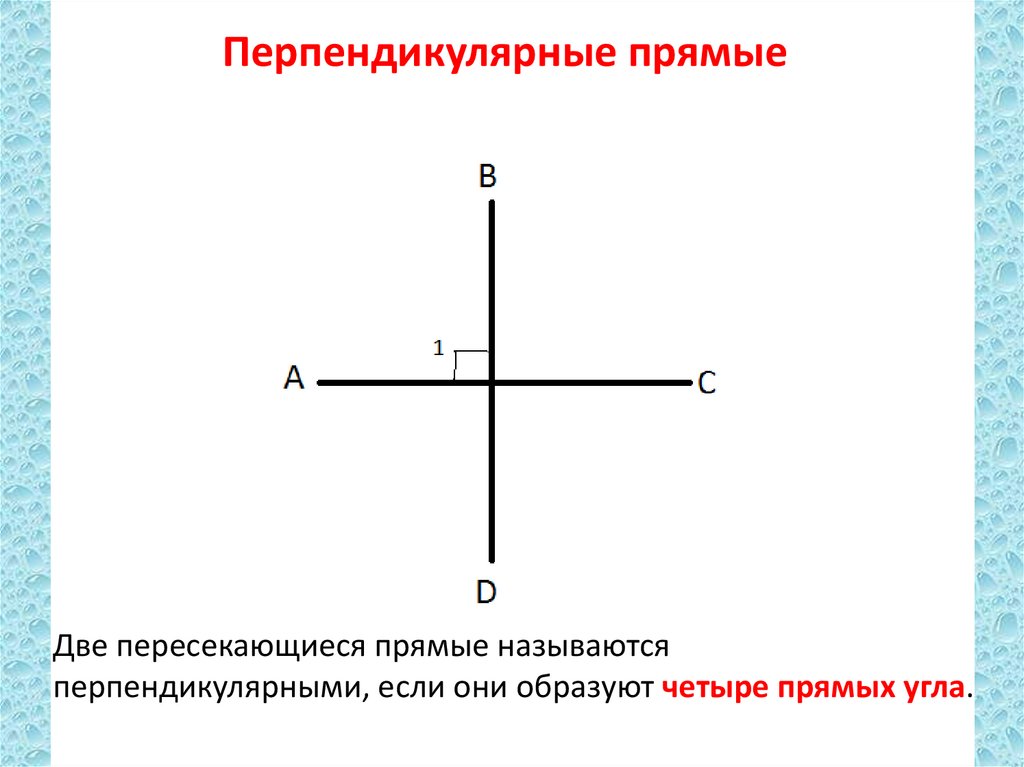
— Обозначают: АС ⊥ ВД.

— Читают: прямая АС перпендикулярна прямой ВД.

— Если АС ⊥ВД, то ВД ⊥ АС

—Показать на доске построение прямых с помощью транспортира и чертежного треугольника.

— В тетрадях проведем наклонную прямую (показываю на доске), строим перпендикулярную к ней с помощью транспортира.

— В тетрадях проведем наклонную прямую, строим перпендикулярную к ней с помощью чертежного треугольника. Обозначим на втором рисунке прямые с помощью маленьких латинских букв а и с .

— Опишите взаимное расположение прямых: a ⊥ с.

— Отметьте по две точки на каждой прямой.

— Какие геометрические фигуры получились? (Отрезки и лучи.)

— Обозначим отрезки как АВ и СD. Что можете о них сказать? (Они перпендикулярны друг другу.)

— Опишите взаимное расположение отрезков: АВ ⊥ CD.

— Дайте определение перпендикулярных отрезков (лучей). Определение. Отрезки (или лучи), лежащие на перпендикулярных прямых, называют перпендикулярными.

VII. Физкультминутка .

VIII. Закрепление изученного материала

1. № 464 стр. 109 (устно).

с ⊥ b, k ⊥ l.

2. № 465 стр. 109 (на доске и в тетрадях).

Вывод: через точку, не лежащую на прямой, можно провести только одну прямую, перпендикулярную данной прямой

IX. Работа над задачей

№ 474 стр. 110 (самостоятельно, устная проверка).

Решение:

1) 60:0,2=300 (м)-осталось в первый раз,

2) 300:0,5 = 600 (м) –было в куске.

Ответ: 600 м.

X. Повторение изученного материала

1. № 469 (а, б) стр. 110 (самостоятельно, взаимопроверка).

— Какое свойство уравнений использовали при решении второго уравнения?

а) 2х – 5 = х + 2

2х - х = 2 + 5

х = 7

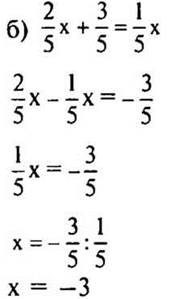
2 способ

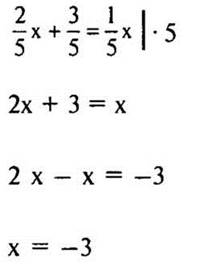
(Ответ: а) х = 7; б) х = —3.)

XI. Подведение итогов урока

— Какие прямые называют перпендикулярными?

— Какие отрезки и лучи называют перпендикулярными?

— Сколько перпендикулярных прямых можно провести к данной прямой из одной точки, не лежащей на этой прямой?

Домашнее задание

№ 476 стр.110, №477 ,№ 480 (в, г) стр. 111.