Просмотр содержимого документа
«Тест 1 Тригонометрические функции»
Тест 1
Тригонометрические функции
Вариант 1
А1. Найдите значение выражения: 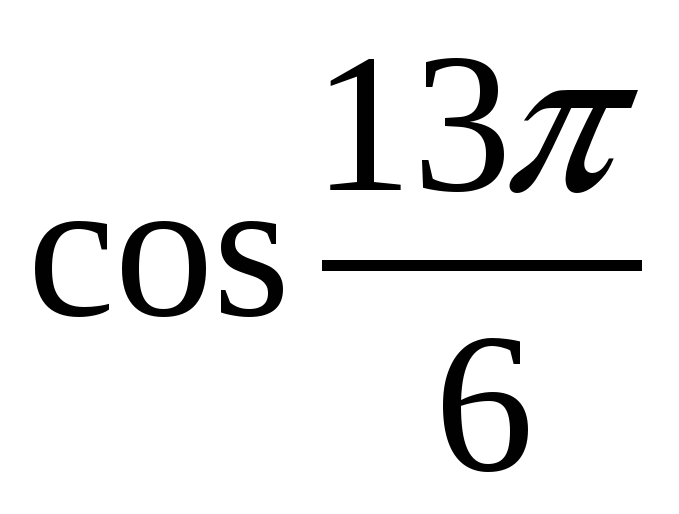 .
.
1)  2)
2)  3)
3) 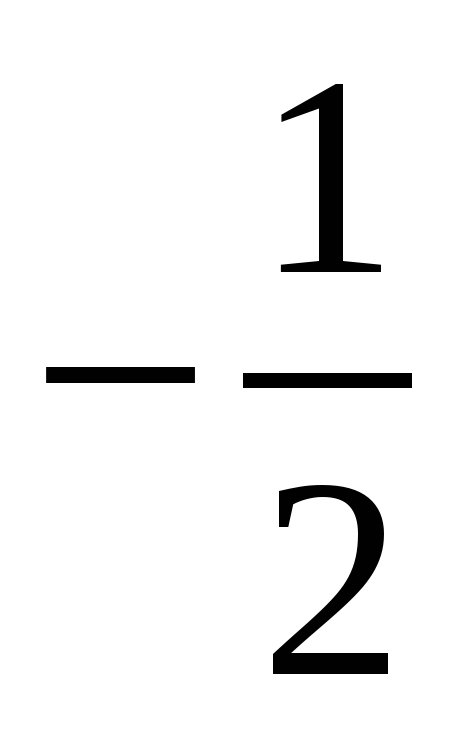 4)
4) 
А2. Найдите значение выражения:  .
.
1)  2)
2) 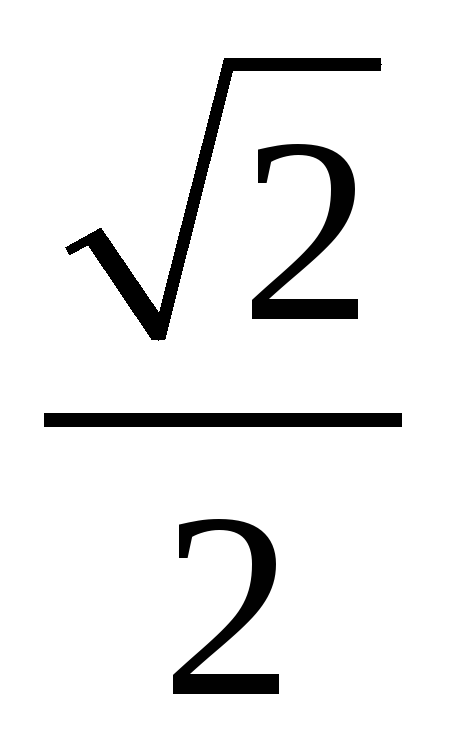 3) 1 4) –1
3) 1 4) –1
А3. Найдите значение выражения:  .
.
1)  2)
2)  3)
3) 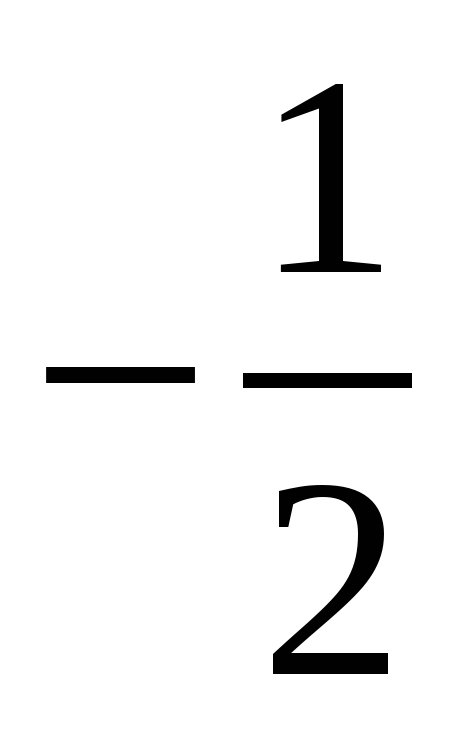 4)
4) 
А4. Найдите значение выражения:  .
.
1)  2) –1 3)
2) –1 3)  4) 1
4) 1
А5. Упростите выражение:  .
.
1)  2)
2)  3)
3)  4)
4) 
А6. Какими свойствами обладает функция  ?
?
1) нечетная, периодическая 2) ни четная ни нечетная, непериодическая
3) четная, периодическая 4) ни четная ни нечетная, периодическая
А7. Найдите наименьший положительный период функции  .
.
1) 2) 3 3)  4)
4) 
А8. Найдите наименьшее значение функции  на отрезке
на отрезке  .
.
1)  2)
2)  3) -1 4)
3) -1 4) 
А9. Какая из точек принадлежит графику функции  ?
?
1)  2)
2)  3)
3)  4)
4) 
А10. Какая из точек не принадлежит графику функции  ?
?
1)  2)
2)  3)
3)  4)
4) 
В1. Сколько целых чисел из промежутка  принадлежит области определения функции
принадлежит области определения функции  ?
?
Тест 1
Тригонометрические функции
Вариант 2
А1. Найдите значение выражения:  .
.
1) 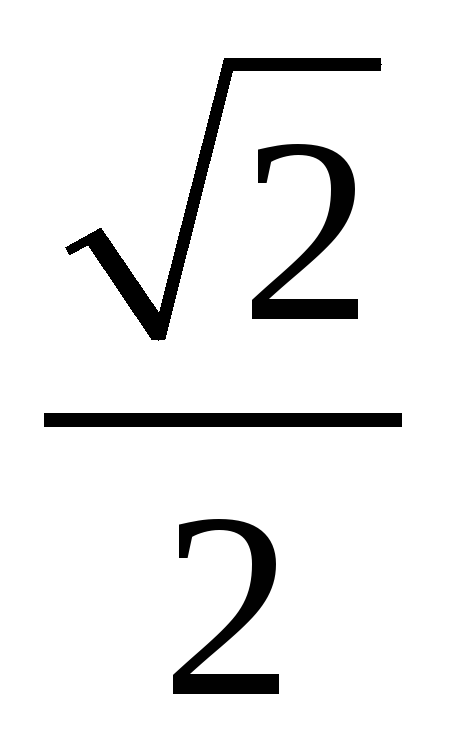 2)
2)  3)
3)  4)
4) 
А2. Найдите значение выражения:  .
.
1)  2)
2) 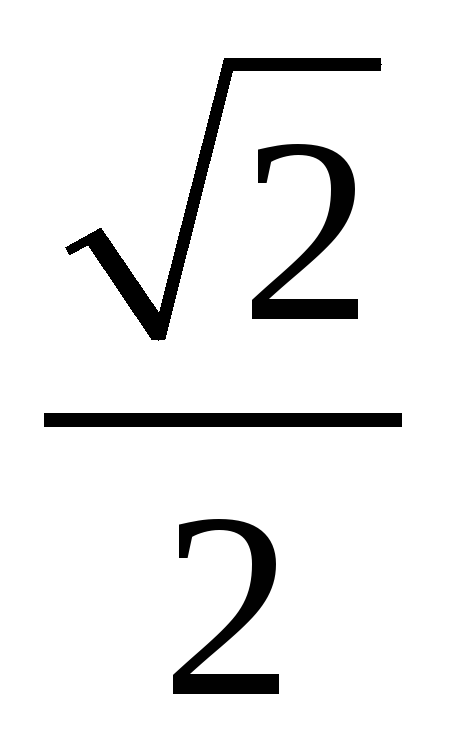 3) 1 4) –1
3) 1 4) –1
А3. Найдите значение выражения: .
1)  2)
2)  3)
3) 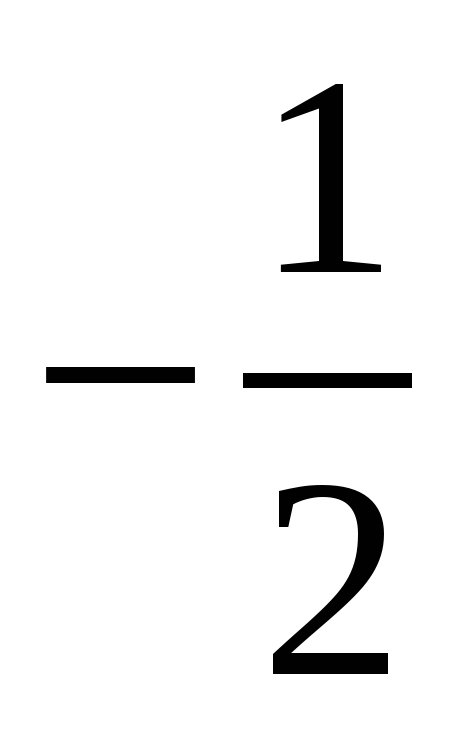 4)
4) 
А4. Найдите значение выражения: .
1)  2) –1 3)
2) –1 3)  4) 1
4) 1
А5. Упростите выражение
1) 1 2) 2cosx 3) 4) cosx+ sinx
А6. Какими свойствами обладает функция у = 3x + cos x.
1) нечетная, периодическая 2) ни четная ни нечетная, непериодическая
3) четная, периодическая 4) ни четная ни нечетная периодическая
А7. Найдите наименьший положительный период функции у = 2sin .
1) 6 2) 3 3)  4)
4) 
А8. Найдите наибольшее значение функции на отрезке .
1) 2) 3) 4)
А9. Какая из точек принадлежит графику функции ?
1) 2) 3)  4)
4)
А10. Какая из точек не принадлежит графику функции ?
1) 2) 3) 4)
В1.Сколько целых чисел из промежутка принадлежит области определения функции ?
Ответы:
| Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | В1 |
| 1 | 1 | 1 | 3 | 2 | 4 | 4 | 3 | 2 | 2 | 4 | 3 |
| 2 | 2 | 4 | 2 | 3 | 3 | 2 | 1 | 1 | 4 | 3 | 5 |
Просмотр содержимого документа
«Тест 2 Тригонометрические уравнения»
Просмотр содержимого документа
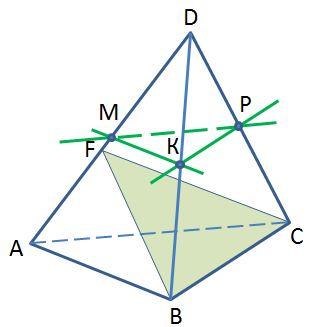
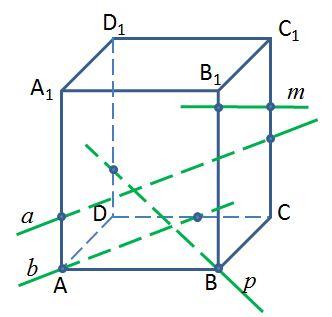
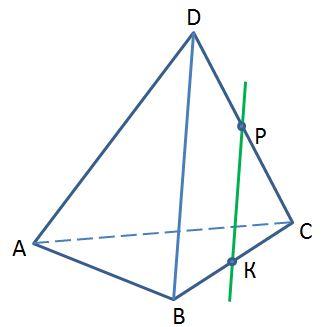
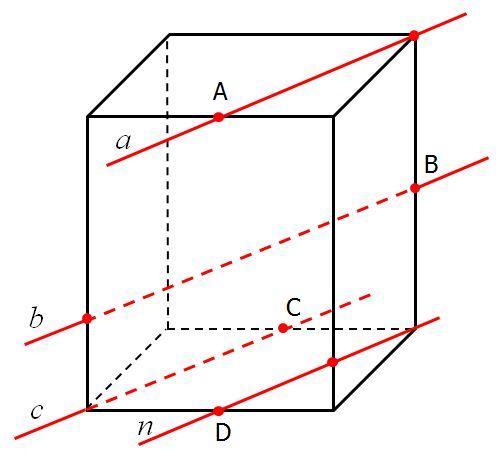
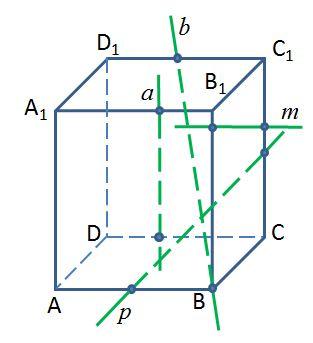
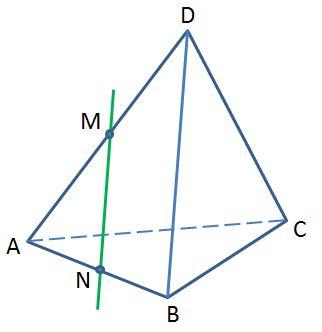
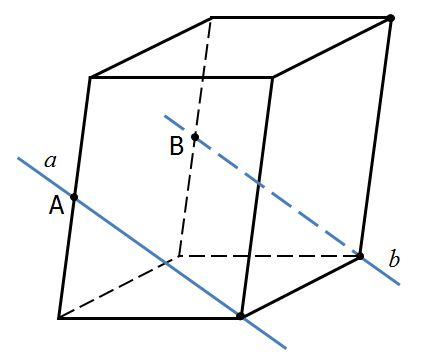
«Тест 2. Параллельность прямых и плоскостей»
Просмотр содержимого документа
«Тест 3 Преобразование тригонометрических выражений»
Тест 3
Преобразование тригонометрических выражений
Вариант 1
А1. Найдите значение выражения:  .
.
1)  2)
2)  3)
3)  4)
4) 
А2. Вычислите: 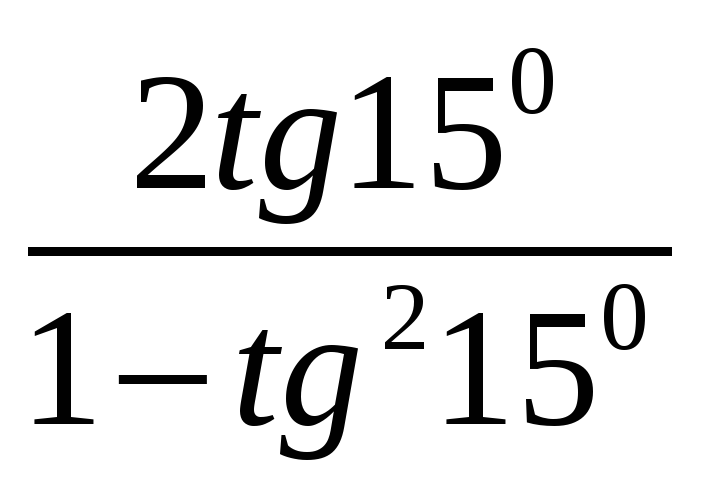
1)  2)
2)  3) 0,5 4)
3) 0,5 4) 
А3. Вычислите: 
1) 
 2) 0,5 3)
2) 0,5 3)  4) 0
4) 0
А4. Упростите выражение: 
1)  2)
2)  3)
3)  4) 1
4) 1
А5. Упростите выражение:  .
.
1)  2)
2)  3) 0; 4)
3) 0; 4)  .
.
А6. Вычислите: 
1) 0 2) -1 3) 2 4) 1
А7. Найдите значение выражения: 
1) 1 2) 2 3) 0 4) -1
А8. Упростите выражение:  .
.
1)  2)
2)  3)
3)  ; 4)
; 4) 
А9. Найдите значение выражения: 
1)  2) 7 3) -7 4)
2) 7 3) -7 4) 
А10. Найдите значение выражения: 
1) 0,25 2) 4 или 0,25 3) -0,25 4) 4
Тест 3
Преобразование тригонометрических выражений
Вариант 2
А1. Найдите значение выражения:  .
.
1)  2)
2)  3)
3)  4)
4) 
А2. Найдите значения выражения cos2α - sin2α , если tgα=2.
1) 1; 2) -1; 3) ; 4)
; 4)  .
.
А3. Упростите выражение 6,8 + 2cos2x, если sinx = .
.
1) 8,3; 2) 7,8; 3) 6,8; 4) 9,3.
А4. Вычислите: 
1) 3 ; 2) 3; 3) 1,5
; 2) 3; 3) 1,5 ; 4)
; 4)  .
.
А5. Упростите выражение 6cos2a – 5 –3cos2a.
1) 1; 2) 2 3) –2; 4) –5.
А6. Упростите выражение 
1) -20,6; 2) -16,4; 3) -19,4; 4) 6cos2α-22,4.
А7. Упростите выражение 7,4 - tg2α, если cosα= .
.
1) 17,4; 2) 4,4; 3) -0,6; 4) -2,6.
А8. Упростите выражение  , если tg x = 4.
, если tg x = 4.
1) 5; 2) 10; 3) 17; 4) 34.
А9. Найдите значение выражения
 .
.
1)  ; 2) 1+
; 2) 1+ ; 3) ; 4)
; 3) ; 4)  .
.
А10. Упростите выражение: , если .
1) 2; 2) 4; 3) 1; 4) 2tg2 α.
Ответы:
| Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
| 1 | 1 | 4 | 4 | 1 | 2 | 2 | 2 | 2 | 4 | 4 |
| 2 | 3 | 4 | 1 | 4 | 3 | 3 | 3 | 4 | 2 | 2 |
Просмотр содержимого документа
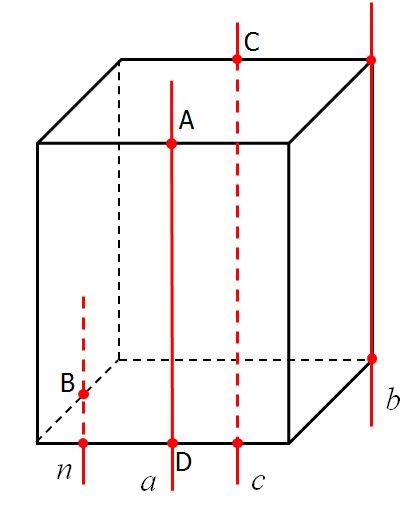
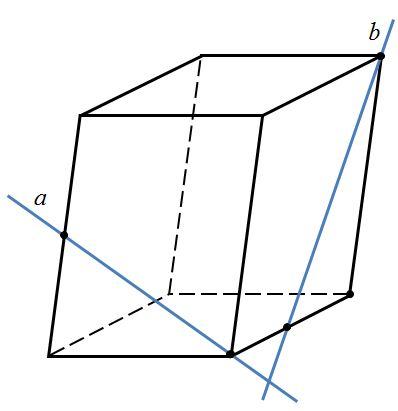
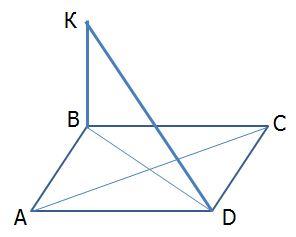
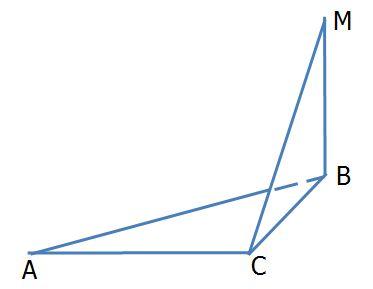
«Тест 3. Перпендикулярность прямых и плоскостей»
Просмотр содержимого документа
«Тест 4 Производная»
Тест 4
Производная
Вариант 1
А1. Найдите производную функции  .
.
1) 12х2 2) 12х 3) 4х2 4) 12х3
А2. Найдите производную функции  .
.
1) -5 2) 11 3) 6 4) 6х
А3. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А4. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А5. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А6. Вычислите значение производной функции  в точке хо=2.
в точке хо=2.
1) 10 2) 12 3) 8 4) 6
А7. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А8. Вычислите значение производной функции  в точке хо= 4.
в точке хо= 4.
1) 21 2) 24 3) 0 4) 3,5
А9. Вычислите значение производной функции 
в точке  . 1) 2 2)
. 1) 2 2)  3) 4 4)
3) 4 4) 
А10. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
В![]() 1. Вычислите значение производной функции
1. Вычислите значение производной функции  в точке хо= 26.
в точке хо= 26.
В2. Найдите значение х, при которых производная функции  равна 0.
равна 0.
Тест 4
Производная
Вариант 2
А1. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А2. Найдите производную функции  .
.
1) 7 2) 12 3) -5 4) -5х
А3. Найдите производную функции  .
.
1)  2)
2)  3)
3)  4)
4) 
А4. Найдите производную функции  .
.
1)  2)
2)  3) 4)
3) 4)
А5. Найдите производную функции .
1)  2) 3) 4)
2) 3) 4)
А6. Вычислите значение производной функции в точке хо=2.
1) 13 2) 3 3) 8 4) 27
А7. Найдите производную функции .
1) 2) 3) 4)
А8. Вычислите значение производной функции в точке .
1) -47 2) -49 3) 47 4) 11,5
А9. Вычислите значение производной функции
в точке . 1) 2 2) -1 3) -2 4)
А10. Найдите производную функции .
1) 2) 3) 4)
В![]() 1. Вычислите значение производной функции в точке хо= -7.
1. Вычислите значение производной функции в точке хо= -7.
В2. Найдите значение х, при которых производная функции равна 0.
Ответы:
| Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 | В1 | В2 |
| 1 | 1 | 3 | 4 | 2 | 3 | 2 | 3 | 1 | 1 | 4 | 2 | 4 |
| 2 | 2 | 3 | 3 | 1 | 4 | 1 | 2 | 2 | 3 | 3 | -9 | -4 |
Просмотр содержимого документа
«Тест 5 Применения производной к исследованию функций»
Тест 6
Применения производной к исследованию функций
Вариант 1
А1. Укажите промежуток, на котором функция  только возрастает.
только возрастает.
1)  2)
2)  3)
3)  4)
4) 
А2. Укажите промежуток, на котором функция  убывает.
убывает.
1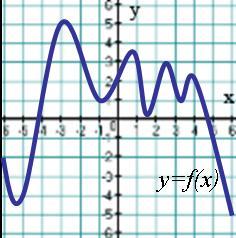 )
)  2)
2)  3)
3)  4)
4) 
А3. На рисунке изображен график функции  . Сколько точек минимума имеет функция?
. Сколько точек минимума имеет функция?
1) 4 2) 5 3) 2 4) 1
А4. Найдите точку максимума функции  .
.
1) -4 2) -2 3) 4 4) 2
А5. Сколько критических точек имеет функция  ?
?
 1) 2 2) 1 3) 4 4) 3
1) 2 2) 1 3) 4 4) 3
А6. На рисунке изображен график производной у =f ´(x).
Найдите точку максимума функции у =f(x).
1) 1 2) 3 3) 2 4) -2
А7. Найдите точку минимума функции  .
.
1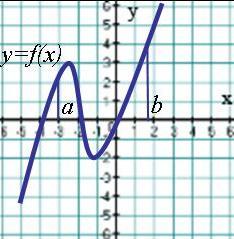 ) -2 2) -0,5 3) 0,5 4) 2
) -2 2) -0,5 3) 0,5 4) 2
А8. График функции у=f(x) изображен на рисунке. Укажите наибольшее значение этой функции на отрезке 
1) 2 2) 3 3) 4 4) 6
А9. Найдите наименьшее значение функции  на отрезке
на отрезке  . 1)
. 1)  2) 3 3) 1 4) -
2) 3 3) 1 4) -
А10. Найдите наименьшее значение функции  .
.
1) -1; 2) -3; 3) -2; 4) - .
.
Тест 6
Применения производной к исследованию функций
Вариант 2
А1. Укажите промежуток, на котором функция  только убывает.
только убывает.
1)  2)
2)  3)
3)  4)
4) 
А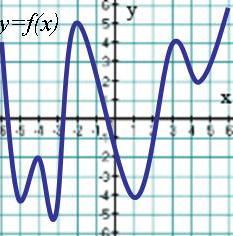 2. Укажите промежуток, на котором функция
2. Укажите промежуток, на котором функция  возрастает.
возрастает.
1)  2)
2)  3)
3)  4)
4) 
А3. На рисунке изображен график функции  . Сколько точек минимума имеет функция?
. Сколько точек минимума имеет функция?
1) 5 2) 3 3) 2 4) 1
А4. Найдите точку максимума функции  .
.
1) -3 2) -2 3) 3 4) 2
А5. Сколько критических точек имеет функция  ?
?
 1) 2 2) 1 3) 4 4) 3
1) 2 2) 1 3) 4 4) 3
А6. На рисунке изображен график производной у =f ´(x).
Найдите точку минимума функции у =f(x).
1) 1 2) 3 3) -4 4) -2
А7. Найдите точку максимума функции  .
.
1 ) -2 2) -0,5 3) 0,5 4) 2
) -2 2) -0,5 3) 0,5 4) 2
А8. График функции у=f(x) изображен на рисунке. Укажите наименьшее значение этой функции на отрезке 
1) 2 2) -2 3) -4 4) 6
А9. Найдите наибольшее значение функции  на отрезке
на отрезке  . 1)
. 1)  2) 3 3) 2 4) 4
2) 3 3) 2 4) 4
А10. Найдите наибольшее значение функции  .
.
1) 1 2) 3 3) 2 4) 
Ответы:
| Вариант | А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 | А9 | А10 |
| 1 | 3 | 2 | 1 | 4 | 1 | 2 | 4 | 3 | 1 | 2 |
| 2 | 2 | 4 | 2 | 1 | 4 | 4 | 2 | 2 | 3 | 1 |





 .
.  ?
?  ?
?  3)
3)  .
.
 .
. .
. .
. .
. .
. .
. .
.  .
.  .
. 

 .
. 




 в точке хо=2.
в точке хо=2.  )
)  1) 2 2) 1 3) 4 4) 3
1) 2 2) 1 3) 4 4) 3 ) -2 2) -0,5 3) 0,5 4) 2
) -2 2) -0,5 3) 0,5 4) 2 .
.  2. Укажите промежуток, на котором функция
2. Укажите промежуток, на котором функция 









