Просмотр содержимого документа
«Теорема Эйлера. Призма.»
Тема: Многогранники. Теорема Эйлера. Призма.
Задание: Записать конспект
Теорема Эйлера: Сумма числа граней и вершин любого многогранника равна числу рёбер, увеличенному на 2. Г + В = Р + 2
Число граней плюс число вершин минус число рёбер в любом многограннике равно 2. Г + В - Р = 2
| Правильный многогранник | Число |
| граней | вершин | рёбер |
| Тетраэдр | 4 | 4 | 6 |
| Куб | 6 | 8 | 12 |
| Октаэдр | 8 | 6 | 12 |
| Додекаэдр | 12 | 20 | 30 |
| Икосаэдр | 20 | 12 | 30 |
ПР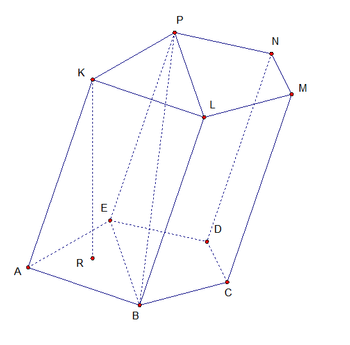 ИЗМА
ИЗМА
Определение. Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки многоугольников.
Основания ABCDE, KLMNP
Боковые грани Все грани, кроме оснований. ABLK, BCML, CDNM, DEPN, EAKP
Боковые ребра AK, BL, CM, DN, EP
Высота KR
Диагональ BP
Диагональное сечение EBLP
основания призмы равны.
у призмы основания лежат в параллельных плоскостях.
у призмы боковые ребра параллельны и равны.
Определение. Призма называется прямой, если ее боковые ребра перпендикулярны основаниям. В противном случае призма называется наклонной.
Оп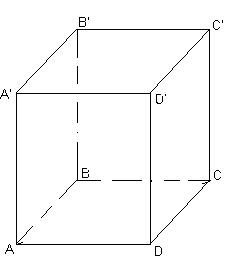 ределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
ределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
Основания правильной призмы являются правильными многоугольниками.
Боковые грани правильной призмы являются равными прямоугольниками.
Боковые ребра правильной призмы равны.
Правильная призма является прямой.





 ИЗМА
ИЗМА ределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.
ределение. Прямая призма называется правильной, если ее основания являются правильными многоугольниками.









