Россия, Нижний Новгород
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 22.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 17.05.2025 09:24
Веселова Светлана Михайловна
Учитель математики
47 лет
4 771
11 193 
Местоположение
Специализация
Теорема косинусов
Категория:
Геометрия
27.12.2021 21:53
Тема:
§ 2. Теорема косинусов
Просмотр содержимого документа
«Теорема косинусов»
Теорема косинусов
А
Геометрия 9 класс
учитель математики
Теорема косинусов
В
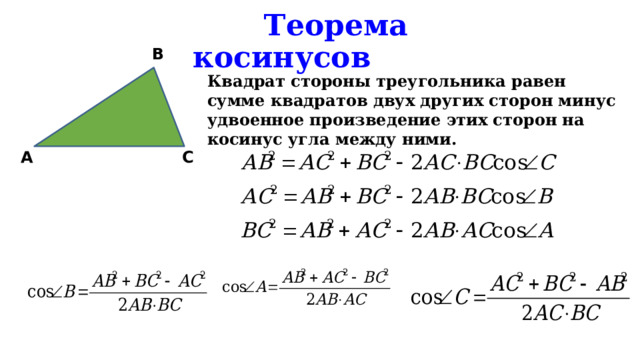
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
А
С
b 2 + c 2 , то треугольник тупоугольный . В а С А " width="640"
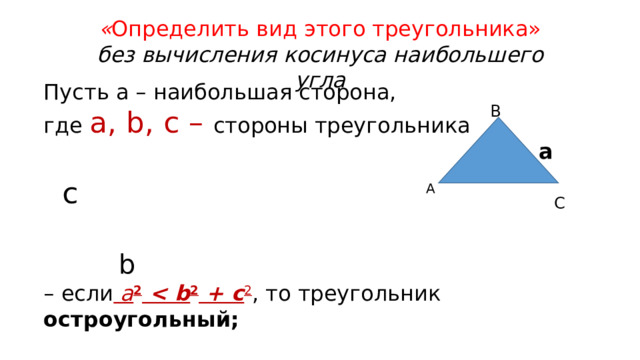
« Определить вид этого треугольника»
без вычисления косинуса наибольшего угла
Пусть a – наибольшая сторона,
где a, b, c – стороны треугольника
c
b – если a 2 2 + c 2 , то треугольник остроугольный;
– если a 2 = b 2 + c 2 , то треугольник прямоугольный;
– если a 2 b 2 + c 2 , то треугольник тупоугольный .
В
а
С
А
N 32
В
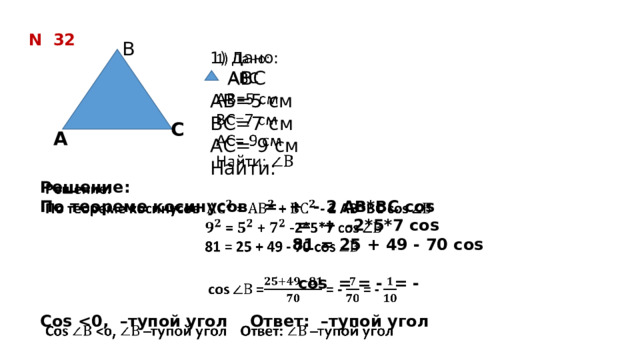
1) Дано:
АВС
АВ=5 см
ВС=7 см
АС= 9 см
Найти:
С
А
Решение:
По теореме косинусов = + - 2 АВ*ВС cos
= + -2*5*7 cos
81 = 25 + 49 - 70 cos
cos = = - = -
Cos Ответ: –тупой угол
В
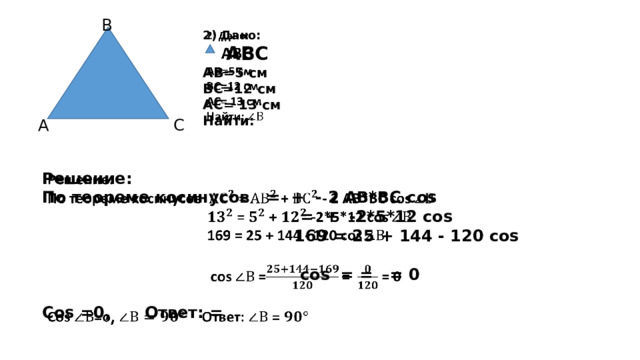
2) Дано:
АВС
АВ=5 см
ВС=12 см
АС= 13 см
Найти:
С
А
Решение:
По теореме косинусов = + - 2 АВ*ВС cos
= + -2*5*12 cos
169 = 25 + 144 - 120 cos
cos = = = 0
Cos =0, Ответ: =
0, –острый угол Ответ : " width="640"
В
3) Дано:
АВС
АВ=10 см
ВС=15 см
АС= 18 см
Найти:
С
А
Решение:
По теореме косинусов = + - 2 АВ*ВС cos
= + -2*10*15 cos
324 = 100 + 225 - 300 cos
cos = =
Cos 0, –острый угол Ответ :
N 30
В
Дано:
АВС
АВ=12 см
ВС=20 см
АС= 28 см
Найти:
С
А
Решение:
По теореме косинусов = + - 2 АВ*ВС cos
= + -2*12*20 cos
784 = 144 + 400 - 480 cos
cos = = - = -
Cos α ◦-60◦= 120◦ Ответ: 120◦
Теорема косинусов
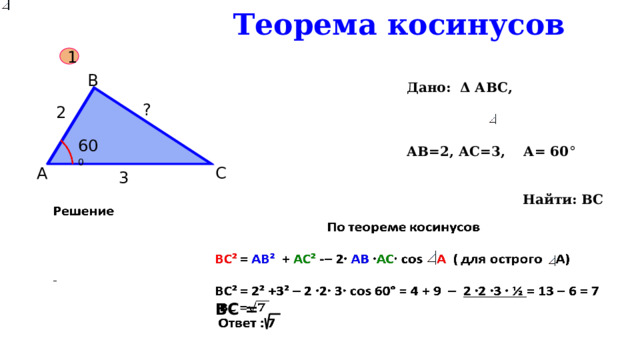
1
В
Дано: Δ АВС,
АВ=2, АС=3, А= 60 °
Найти: ВС
?
2
60 0
60 0
С
А
3
BC =
Теорема косинусов
Дано: ΔАВС,
АВ=2, АС=3, А= 120°
Найти: ВС
2
В
?
2
120◦
А
С
3
Решение
По теореме косинусов ВС² = АВ² + АС² ─ 2 ∙ АВ ∙ АС ∙ соs А , т. к А=120° (тупой угол) и
соs 120 ° = ─ соs 60° , то
ВС² = АВ² + АС² ─ 2 ∙ АВ ∙ АС ∙ соs (180° -60°) = АВ² + АС² + 2 ∙ АВ ∙ АС ∙ соs 6 0° = 2² + 3² + 2 ∙ 2 ∙ 3∙ − = 13 +6=19
__
Ответ: √ 19
Теорема косинусов
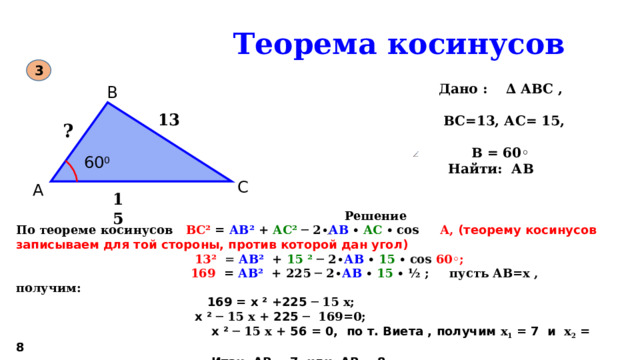
3
Дано : ∆ АВС ,
ВС=13, АС= 15,
В = 60◦
Найти: АВ
В
60 0
13
?
С
А
15
Решение
По теореме косинусов ВС² = АВ² + АС² ─ 2 ∙ АВ ∙ АС ∙ соs А, (теорему косинусов записываем для той стороны, против которой дан угол)
13² = АВ² + 15 ² ─ 2 ∙ АВ ∙ 15 ∙ соs 60◦;
169 = АВ² + 225 ─ 2 ∙ АВ ∙ 15 ∙ ½ ; пусть АВ=х , получим:
169 = х ² +225 ─ 15 х;
х ² ─ 15 х + 225 ─ 169=0;
х ² ─ 15 х + 56 = 0, по т. Виета , получим х 1 = 7 и х 2 = 8
Итак, АВ = 7 или АВ = 8
Ответ: 7 или 8
© 2021, Веселова Светлана Михайловна 3038 24
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
