Муниципальное бюджетное общеобразовательное учреждение
«Ванаварская средняя школа»
Эвенкийского района Красноярского края
Индивидуальный итоговый проект
«Теорема Пифагора и ее применение
в жизни человека»
Выполнил:
Шилов Матвей,ученик 8 «А» класса
Куратор: Привалихина Л.Г.,
учитель математики
с. Ванавара, 2021 год
Содержание проекта
-
Цель и задачи проекта.
-
Практическая значимость проекта.
-
История открытия теоремы Пифагора.
-
Исторические задачи.
-
Области применения теоремы Пифагора.
-
Заключение.
Практическая значимость проекта
Данный проект можно использовать для получения дополнительных знаний по геометрии на внеклассных занятиях по математике
Цель проекта: Выявить основные области применения теоремы Пифагора в практической деятельности человека.
Задачи:
1.Изучить историю открытия теоремы Пифагора.
2.Исследовать области её применения в жизни человека.
3.Привести примеры решения практических задач с применением теоремы Пифагора.
Гипотеза: Теорема Пифагора - очень важное открытие для человечества.
Важным условием развития многих областей науки и техники является внедрение математических методов для качественного и количественного исследования. Теорема Пифагора-одна из важнейших теорем математики, она позволяет решить многие практические задачи и сегодня.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.
Пифагор – древнегреческий философ, математик, астроном. Обосновал
многие свойства геометрических фигур, разработал математическую теориючисел и их пропорций. Внёс значительный вклад в развитие астрономии иакустики. Автор «Золотых стихов», основатель пифагорейской школы вКротоне.
По преданию Пифагор родился около 580 г. до н. э. на острове Самос в
богатой купеческой семье. Его мать – Пифазис, получила свое имя в честь
Пифии, жрицы Аполлона.
Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так, в Египте, при строительстве сооружений, учитывалось соотношение сторон прямоугольного треугольника пять тысячелетий назад. В вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора. Возникает вопрос, почему тогда гласит история – возникновения теоремы Пифагора принадлежит ему? Ответ может быть только один – он доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем.
История открытия теоремы
Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: «Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4».
Кантор (крупнейший немецкий историк математики) считает, что равенство 3² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя АменемхетаI .
По мнению Кантора гарпедонапты, или «натягиватели веревок», строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.
Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод: «Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку.»Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии около 18 в до н.э.
В некоторых списках «Начал» Евклида эта теорема назвалась «теоремой нимфы» за сходство чертежа с пчелкой, бабочкой(«теорема бабочки»), что по гречески называлось нимфой. Этим словом греки назвали еще некоторых богинь, а также молодых женщин и невест. Арабский переводчик не обратил внимания на чертеж и перевел слово «нимфа» как «невеста». Так появилось ласковое название «теорема невесты». Существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Отсюда еще одно название- «теорема ста быков».
В англоязычных странах ее назвали: «ветряная мельница», «павлиний хвост», «кресло невесты», «ослиный мост» (если ученик не мог через него перейти», значит, он был настоящим « ослом»).
В дореволюционной России рисунок теоремы Пифагора для случая равнобедренного треугольника называли «пифагоровыми штанами». Эти «штаны» появляются, когда на каждой стороне прямоугольного построить квадраты во внешнюю сторону.
Существует более 350 различных доказательств теоремы Пифагора. За это она попала в Книгу рекордов Гиннеса.
Исторические задачи.
-
Задача индийского математика XII века Бхаскары
"На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?"
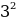 +
+ 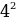 =
= 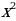
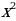 = 25
= 25
X = 5(футов) – длина отломленной части ствола;
3 + 5 = 8(футов) – высота тополя
-
Задача из учебника "Арифметика" Леонтия Магницкого
Случися некоему человеку к стене лествицу
прибрати, у стены же тоя высота есть 117 стоп.
И обретете лестницу долготью 125 стоп.
И ведати хощет, колико стоп сея лествицы
нижний конец от стены отстояти имать.

Применение в строительстве.
Пример 1.
Вычисление длины стропил при строительстве крыши.
При строительстве домов и коттеджей часто встает вопрос о длине стропил, если уже изготовлены балки.
В доме задумано построить двускатную крышу(форма в сечении). Какой длины должны быть стропила, если изготовлены балки AD=3м, DC=6м,BD=4м.
Решение:
1)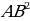 =
=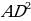 +
+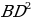
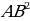 =
=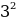 +
+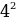 =9+16=25
=9+16=25
AB=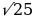 =5м
=5м
2)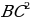 =
=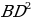 +
+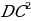
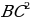 =
=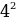 +
+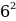
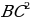 =16+36=52м
=16+36=52м
BC=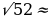 7,2м
7,2м
Ответ:AB=5м,BC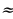 7,2м
7,2м
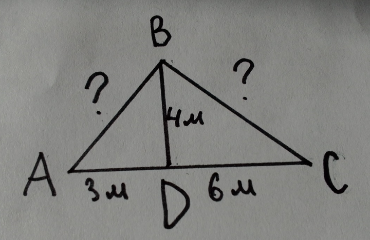
Пример 2.
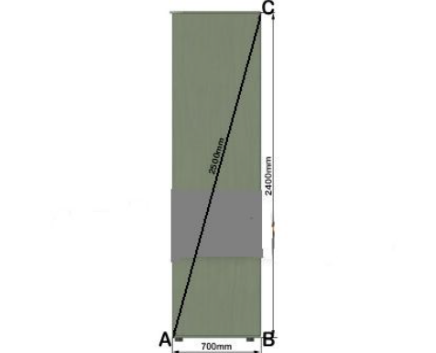
Расчетные задачи при изготовлении мебели.
AB=700мм, BC=2400мм.
Найти:AC.
 =
=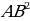 +
+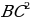
 =
= +
+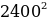
 =490000+5760000=6250000
=490000+5760000=6250000
AC=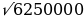 =2500мм
=2500мм
Ответ:AC=2500мм
Пример 3.
Необходимо закрепить трубу на школьной котельной угольниками. Один конец угольника должен крепиться на высоте 3м, другой на земле на расстоянии 2 м от трубы. Определить сколько метров угольника понадобится для того, чтобы закрепить трубу.
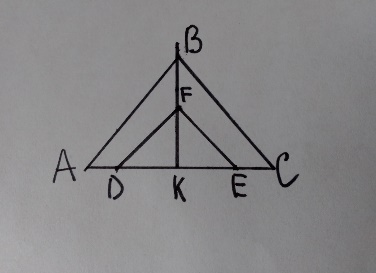
DK=KE=2м,FK=3м.
 =
=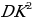 +
+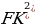
 =
=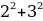
 =4+9=13
=4+9=13
DF=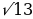
DF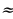 3,6м
3,6м
Ответ: DF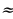 3,6м.
3,6м.
Пример 4.
Брус наибольшего объема.
Задача
Из цилиндрического бревна надо выпилить прямоугольный брус
наибольшего объема. Какой формы должно быть его сечение (рис. 23)?
Решение
Если стороны прямоугольного сечения х и y, то по теореме Пифагора
x²+ y²= d²,
где d - диаметр бревна. Объем бруса наибольший, когда площадь его сечения наибольшая, т. е. когда ху достигает наибольшей величины. Но если ху наибольшее, то наибольшим будет и произведение x²y².Так как сумма x²+ y²неизменна, то, по доказанному ранее, произведение x²y²наибольшее, когда
x²= y²или х = y.
Итак, сечение бруса должно быть квадратным.
Применение в архитектуре.
В зданиях романского и готического стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
Если b обозначает ширину окна, то радиусы полуокружностей будут равны R=b/2 и r =b/4. Радиус р внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рисунке цветом . Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+ р, один катет равен b/4, а другой b/2- р. По теореме Пифагора имеем:
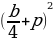 =
=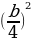 +(
+(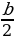 - р)
- р)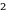
откуда
b* 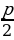 =
=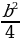 - b р .
- b р .
Разделив на b приводя подобные члены, получим:
3* 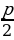 =
=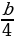 , р =
, р =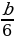 , т.е. радиус р внутренней окружности =
, т.е. радиус р внутренней окружности = 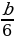
Применение в геометрии
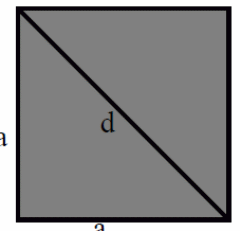 Диагональ dквадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Тогда d²=a²+a².
Диагональ dквадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Тогда d²=a²+a².
d²=2a².
d=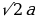
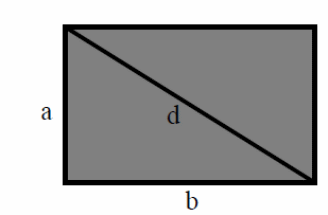
Диагональ dпрямоугольника со сторонами aи bвычисляется подобно тому, как вычисляется гипотенуза прямоугольного треугольника с катетами aи b. Тогда:
d²=a²+b², d=√a²+b².
С помощью теоремы Пифагора можно вычислить и диагональ куба:
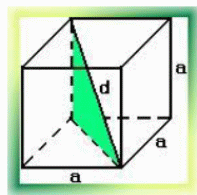
d=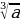
Применение в физике.
Задачи в курсе физики средней школы требуют знания теоремы Пифагора.
Это задачи, связанные со сложением скоростей.
В практическом смысле её можно сформулировать так: под каким углом к
течению реки должен двигаться катер, осуществляющий перевозку
пассажиров между пристанями, чтобы уложиться в расписание (пристани
находятся на противоположных берегах реки)
Молниеотвод - устройство для зданий, промышленных, транспортных, коммунальных и других сооружений от ударов молнии. Молниеотвод защищает от молнии все предметы, расстояние которых от его основания не превышает его удвоенный высоты.
Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
По теореме Пифагора h²≥ a² + b²
Значит, h≥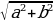 .
.
Теорема Пифагора и спорт.

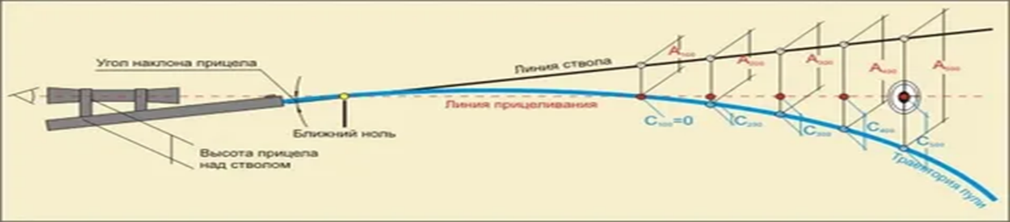
Когда биатлонист стреляет по мишени, он делает «поправку на ветер».
Если ветер дует справа, а спортсмен стреляет по прямой, то пуля уйдёт
влево. Чтобы попасть в цель, надо сдвинуть прицел вправо на расстояние
смещения пули. Для них составлены специальные таблицы (на основе
следствий из т. Пифагора). Биатлонист знает, на какой угол смещать прицел
при известной скорости ветра.
Астрономия – также широкая область для применения теоремы.
Путь светового луча. Какой путь проходит луч? Свет идет туда и обратно одинаковый путь.
Чему равна половина пути, который проходит луч? Если обозначить отрезок
AB символом l, половину времени как t, а также обозначив скорость
движения света буквой c, то наше уравнение примет вид
c * t = l
Это ведь произведение затраченного времени на скорость!

Явление звёздной аберрации, открытое в 1729 году, заключается в том, что
все звёзды на небесной сфере описывают эллипсы. Большая полуось этих
эллипсов наблюдается с Земли под углом, равным 20,5 градуса. Такой угол
связан с движением Земли вокруг Солнца со скоростью 29,8 км в час. Чтобы
с движущейся Земли наблюдать звезду, необходимо наклонить трубу
телескопа вперёд по движению звезды, так как пока свет проходит длину
телескопа, окуляр вместе с землёй перемещается вперёд. Сложение
скоростей света и Земли производится векторно, используя теорему
Пифагора.
В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными).
Естественно, что вопрос о том, можно ли с помощью световых сигналов
объясняться с этими гипотетическими существами, вызвал оживленную
дискуссию. Парижской академией наук была даже установлена премия в
100000 франков тому, кто первый установит связь с каким-нибудь
обитателем другого небесного тела; эта премия все еще ждет счастливца. В
шутку, хотя и не совсем безосновательно, было решено передать обитателям
Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт,
выражаемый теоремой Пифагора, имеет место всюду, и поэтому похожие на
нас обитатели другого мира должны понять такой сигнал.
Мобильная связь
Кто в современном мире не пользуется сотовым телефоном? Каждый абонент мобильной связи заинтересован в ее качестве. А качество в свою очередь
зависит от высоты антенны мобильного оператора.
Чтобы рассчитать, в каком радиусе можно принимать передачу, применяем теорему Пифагора.
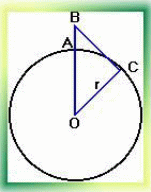 (ОА +АВ)² = ОС² + ВС²
(ОА +АВ)² = ОС² + ВС²
Заключение.
Я считаю, что теорема Пифагора настолько известна, что трудно представить себе человека, не слышавшего о ней. Я изучил ряд исторических и математических источников, в том числе информацию в Интернете, и увидел, что теорема Пифагора интересна не только своей историей, но и тем, что она занимает важное место в жизни и деятельности человека. Она применяется во многих областях науки и техники.
Заслуга Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.
Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема.
В заключении теореме Пифагора можно дать характеристику тремя качествами: красота, простота, значимость.
Убежден, что каждый образованный человек должен знать и применять теорему Пифагора.
Список литературы:
1. Геометрия: учебник для 7-9 кл. сред. Школы /авт.-сост. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. - 4-е изд. - М.: Просвещение, 2004. - 335 с.
2. Энциклопедический словарь юного математика / сост. А. П. Савин. - М.: Педагогика, 1989. - 352 с.
3.Глейзер Г. И. История математики в школе. М., 1982
4. http://th-pif.narod.ru/pract.htm






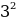 +
+ 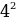 =
= 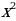

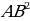 =
=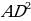 +
+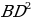
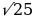 =5м
=5м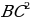 =
=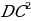
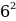
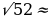 7,2м
7,2м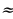 7,2м
7,2м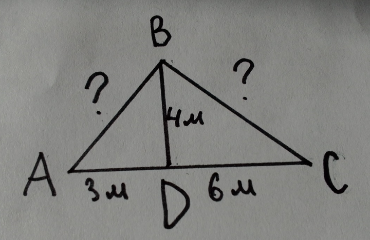
 =
= +
+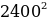
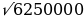 =2500мм
=2500мм

 =
=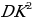 +
+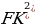
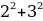
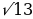
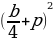 =
=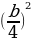 +(
+(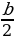 - р)
- р)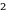
 =
=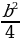 - b р .
- b р .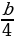 , р =
, р =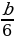 , т.е. радиус р внутренней окружности =
, т.е. радиус р внутренней окружности =  Диагональ dквадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Тогда d²=a²+a².
Диагональ dквадрата со стороной a можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом a. Тогда d²=a²+a².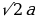


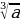
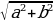 .
.



 (ОА +АВ)² = ОС² + ВС²
(ОА +АВ)² = ОС² + ВС²



















