
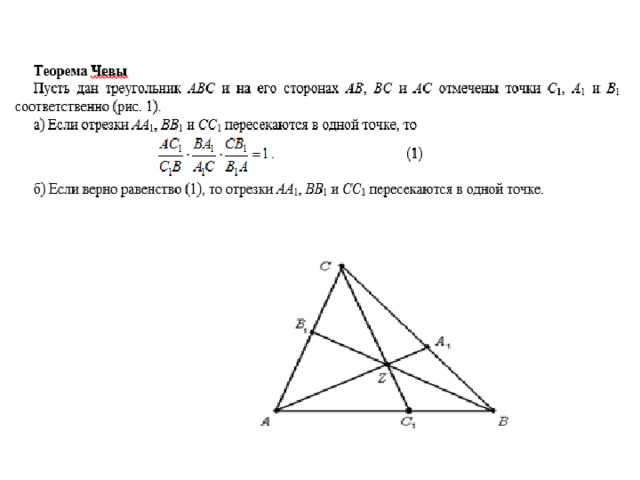
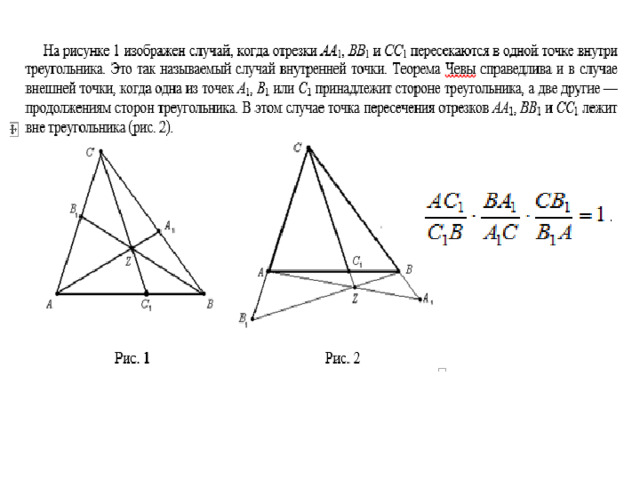
Тема урока: Теоремы Менелая и Чевы

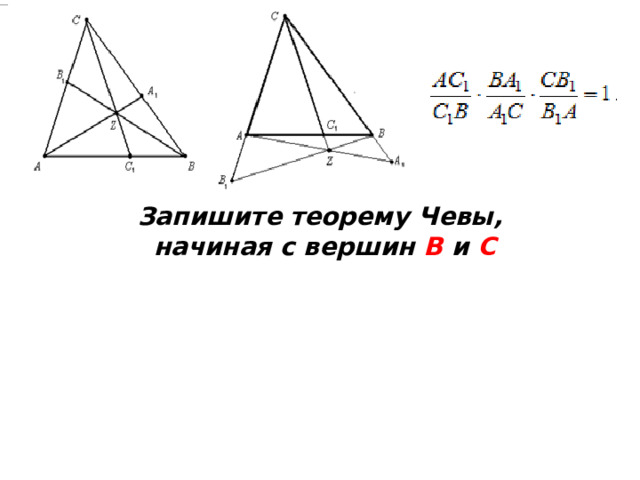
Запишите теорему Чевы,
начиная с вершин В и С
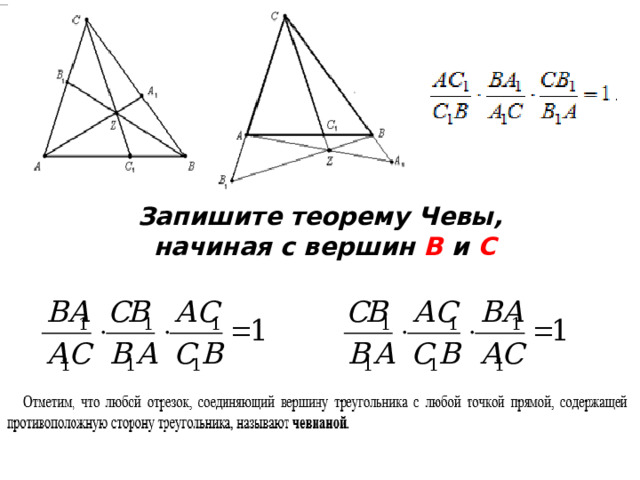
Запишите теорему Чевы,
начиная с вершин В и С
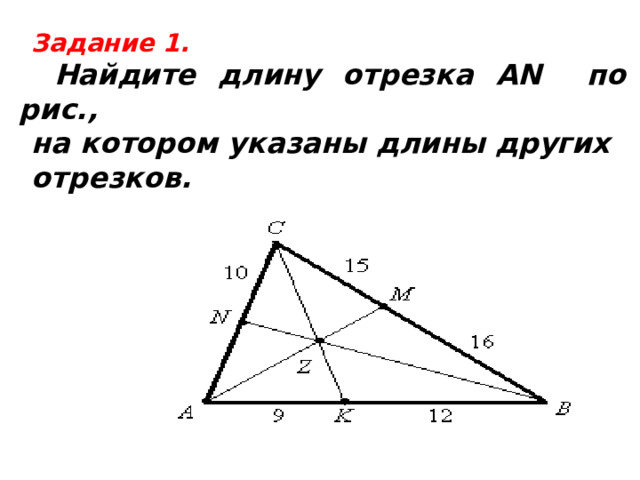
Задание 1.
Найдите длину отрезка АN по рис.,
на котором указаны длины других
отрезков.

Задание 1.
Найдите длину отрезка АN по рис.,
на котором указаны длины других
отрезков.
Решение.
Используем теорему Чевы, начиная
с вершины А:
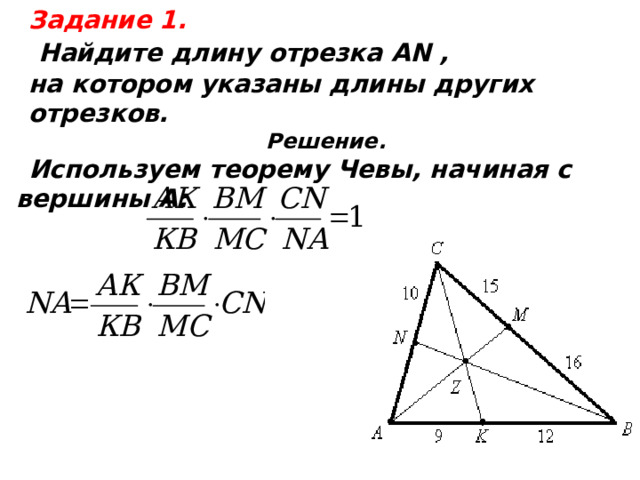
Задание 1.
Найдите длину отрезка АN ,
на котором указаны длины других
отрезков.
Решение.
Используем теорему Чевы, начиная с вершины А:
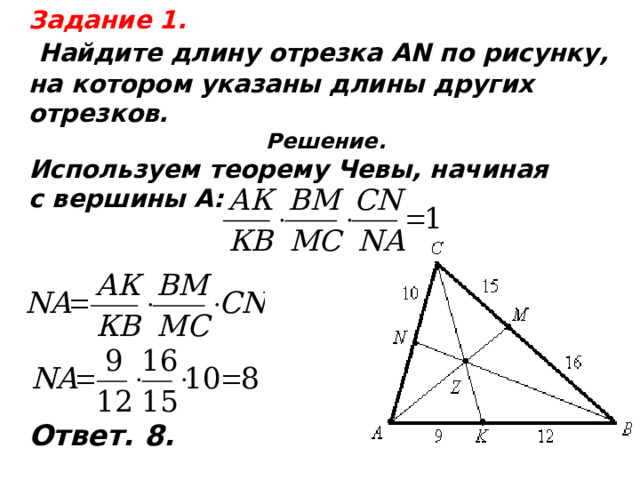
Задание 1.
Найдите длину отрезка АN по рисунку,
на котором указаны длины других
отрезков.
Решение.
Используем теорему Чевы, начиная
с вершины А:
Ответ. 8.
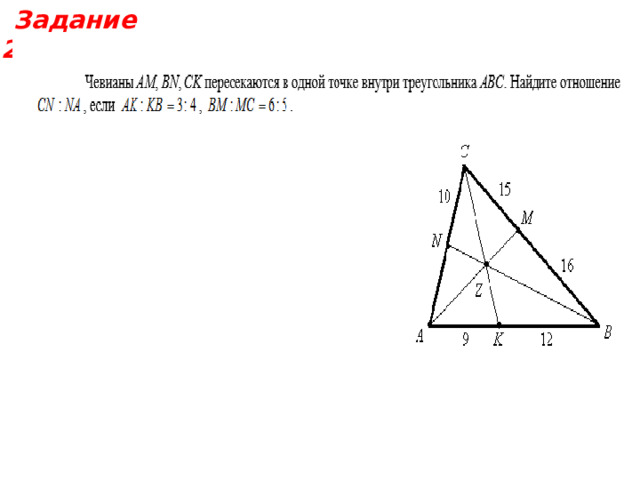
Задание 2.

Решение: Используем теорему Чевы,
начиная с вершины А:

Решение: Используем теорему Чевы,
начиная с вершины А:

Решение: Используем теорему Чевы,
начиная с вершины А:
Ответ: 10:9.
Задание 3.
Отношение площадей двух
треугольников с общей вершиной и
основаниями, лежащими на одной
прямой, равно отношению длин
этих оснований. ( Докажите это утверждение).
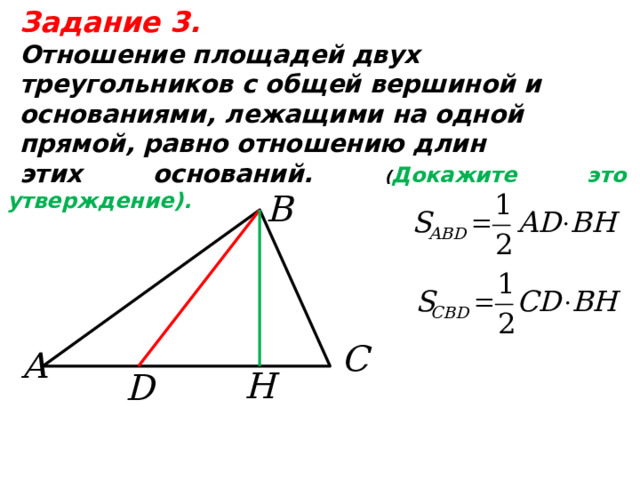
Задание 3.
Отношение площадей двух
треугольников с общей вершиной и
основаниями, лежащими на одной
прямой, равно отношению длин
этих оснований. ( Докажите это утверждение).
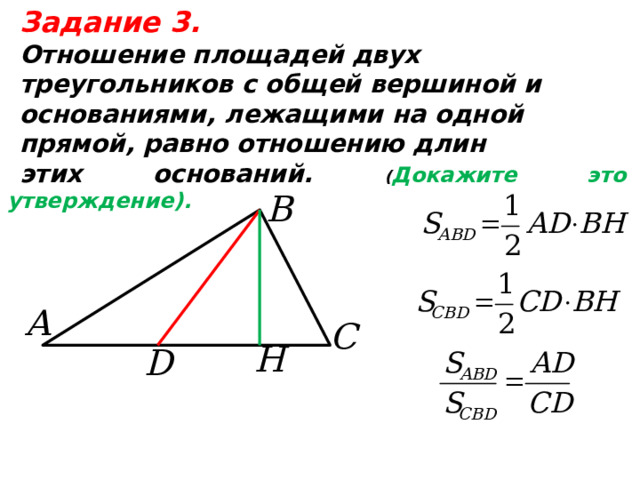
Задание 3.
Отношение площадей двух
треугольников с общей вершиной и
основаниями, лежащими на одной
прямой, равно отношению длин
этих оснований. ( Докажите это утверждение).
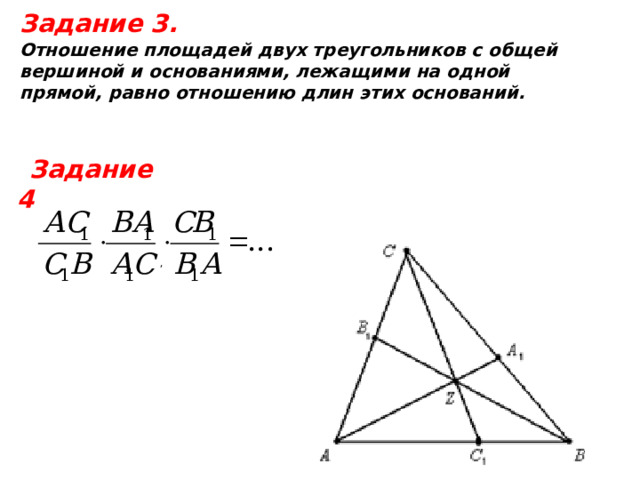
Задание 3.
Отношение площадей двух треугольников с общей
вершиной и основаниями, лежащими на одной
прямой, равно отношению длин этих оснований.
Задание 4
,
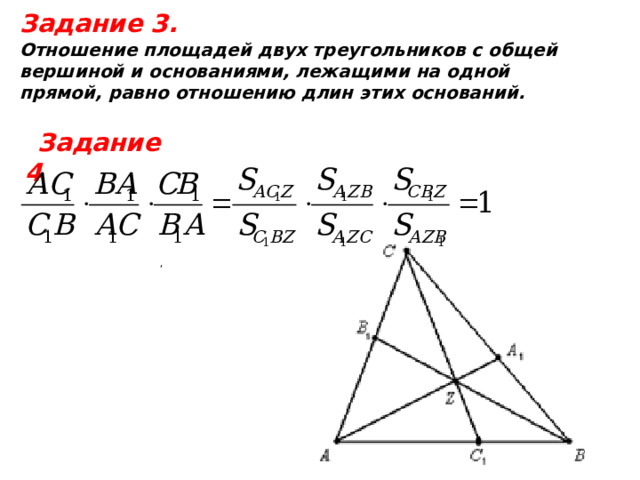
Задание 3.
Отношение площадей двух треугольников с общей
вершиной и основаниями, лежащими на одной
прямой, равно отношению длин этих оснований.
Задание 4
,
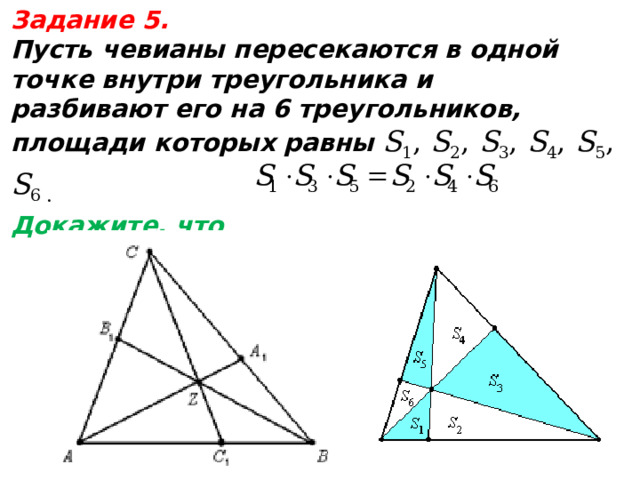
Задание 5.
Пусть чевианы пересекаются в одной
точке внутри треугольника и
разбивают его на 6 треугольников,
площади которых равны S 1 , S 2 , S 3 , S 4 , S 5 , S 6 .
Докажите, что
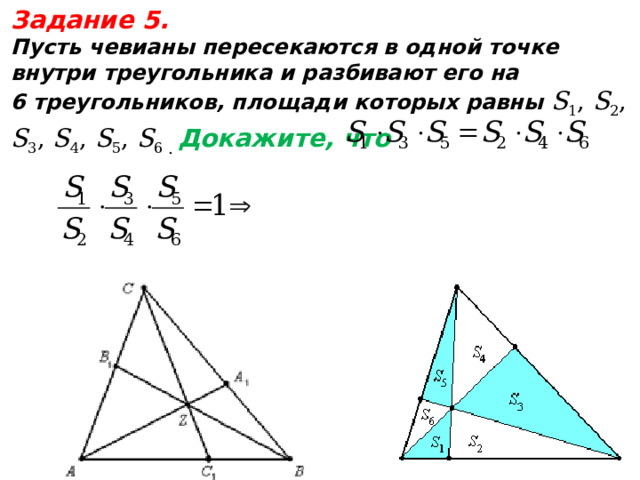
Задание 5.
Пусть чевианы пересекаются в одной точке
внутри треугольника и разбивают его на
6 треугольников, площади которых равны S 1 , S 2 , S 3 , S 4 , S 5 , S 6 . Докажите, что
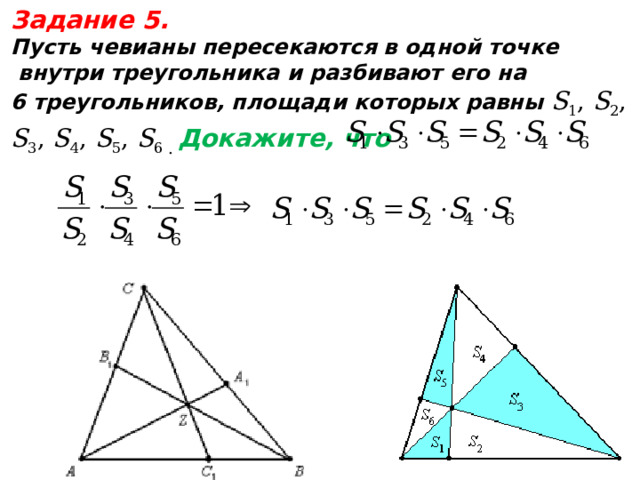
Задание 5.
Пусть чевианы пересекаются в одной точке
внутри треугольника и разбивают его на
6 треугольников, площади которых равны S 1 , S 2 , S 3 , S 4 , S 5 , S 6 . Докажите, что
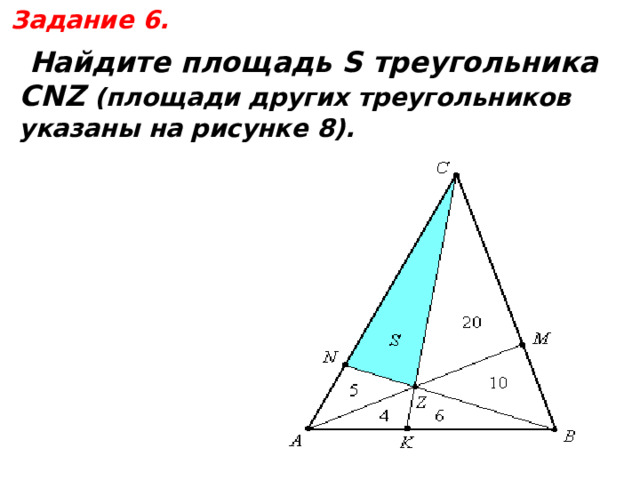
Задание 6.
Найдите площадь S треугольника
CNZ (площади других треугольников
указаны на рисунке 8).
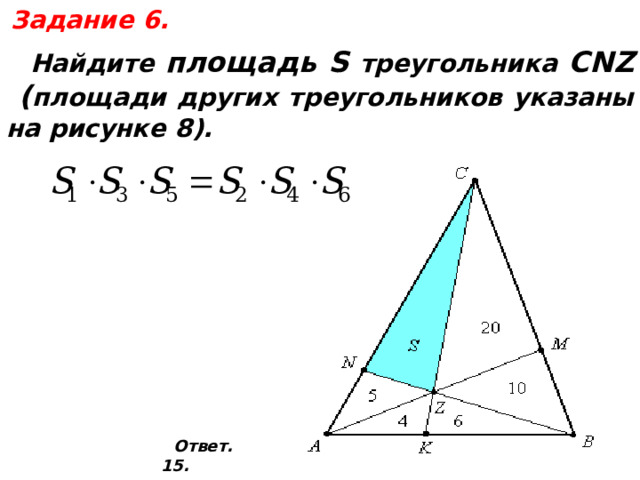
Задание 6.
Найдите площадь S треугольника CNZ
( площади других треугольников указаны на рисунке 8).
Ответ. 15.
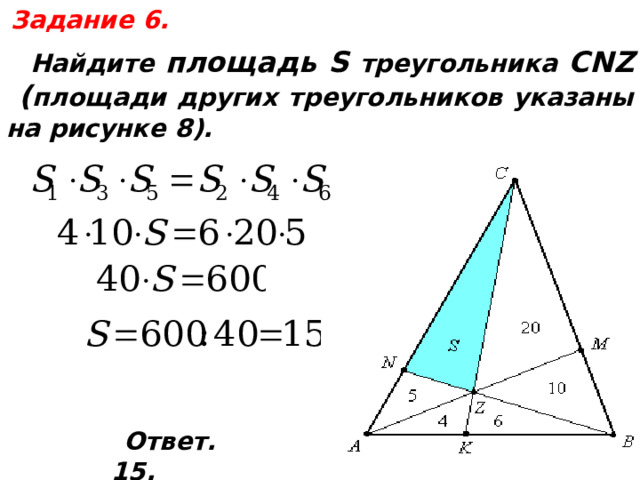
Задание 6.
Найдите площадь S треугольника CNZ
( площади других треугольников указаны на рисунке 8).
Ответ. 15.
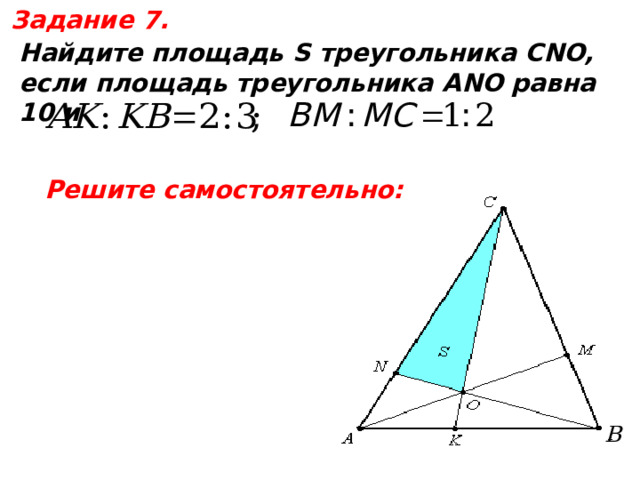
Задание 7.
Найдите площадь S треугольника CNO,
если площадь треугольника АNO равна 10 и
Решите самостоятельно:
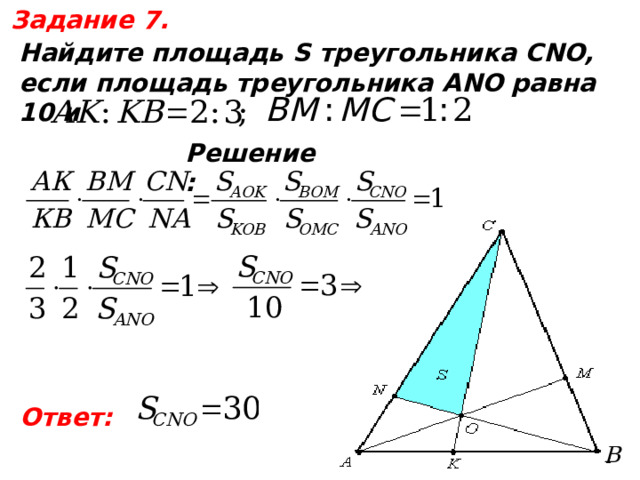
Задание 7.
Найдите площадь S треугольника CNO,
если площадь треугольника АNO равна 10 и
Решение:
Ответ:

Разобрать дома

Задание 9. В треугольнике ABC точки K и L принадлежат соответственно сторонам
AB и BC .
P - точка пересечения отрезков AL и CK.
Площадь треугольника PBC равна 1.
Найдите площадь треугольника ABC.
Решить дома
Ответ: 1,75
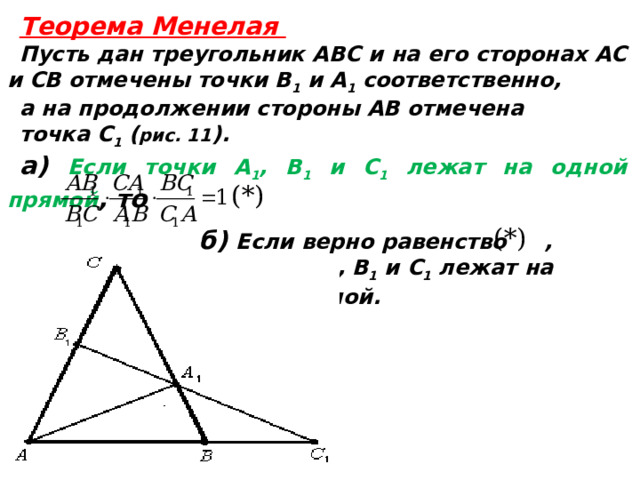
Теорема Менелая
Пусть дан треугольник ABC и на его сторонах AC и CВ отмечены точки B 1 и A 1 соответственно,
а на продолжении стороны AB отмечена
точка C 1 ( рис. 11 ).
а) Если точки А 1 , B 1 и С 1 лежат на одной прямой , то
б) Если верно равенство ,
то точки А 1 , B 1 и С 1 лежат на
одной прямой.

Как запомнить равенство Менелая?
Прием запоминания равенства Менелая
тот же, что и для равенства Чевы.
Вершины треугольника в каждом
отношении и сами отношения
записываются в направлении
обхода вершин треугольника ABC —
от вершины к вершине, проходя
через точки
деления (внутренние или внешние).

Задание 10.
Докажите, что при записи равенства (*) от любой вершины треугольника в любом направлении получается один и тот же
результат.
Решить задачу дома.

Задание 11 .
В треугольнике АВС точки А 1 , В 1 лежат
соответственно на сторонах ВС и AС.
P — точка пересечения отрезков АА 1 и ВВ 1
Найдите отношение:
Разбираем задачу по готовому решению
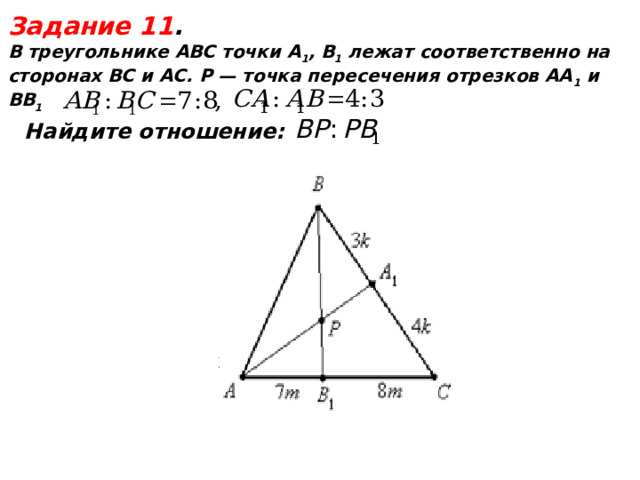
Задание 11 .
В треугольнике АВС точки А 1 , В 1 лежат соответственно на
сторонах ВС и AС. P — точка пересечения отрезков АА 1 и ВВ 1
Найдите отношение:
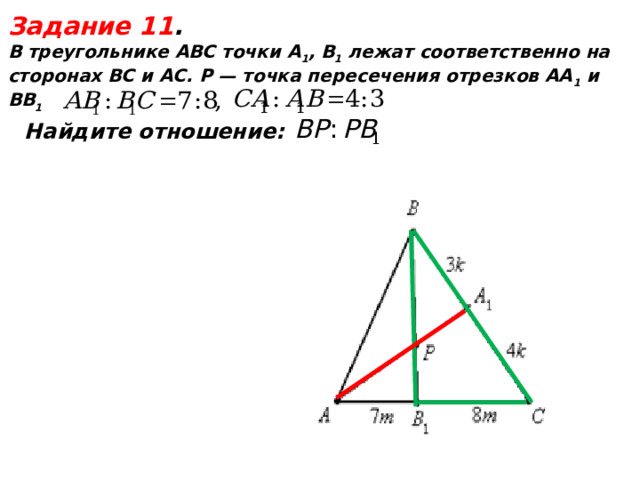
Задание 11 .
В треугольнике АВС точки А 1 , В 1 лежат соответственно на
сторонах ВС и AС. P — точка пересечения отрезков АА 1 и ВВ 1
Найдите отношение:

Задание 11 .
В треугольнике АВС точки А 1 , В 1 лежат соответственно на
сторонах ВС и AС. P — точка пересечения отрезков АА 1 и ВВ 1
Найдите отношение:
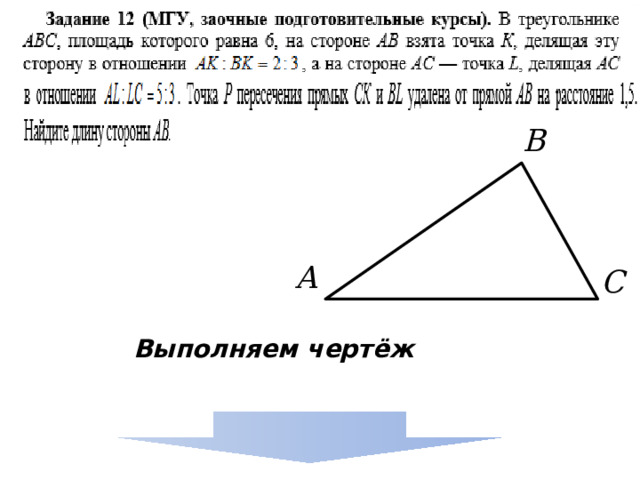
Выполняем чертёж
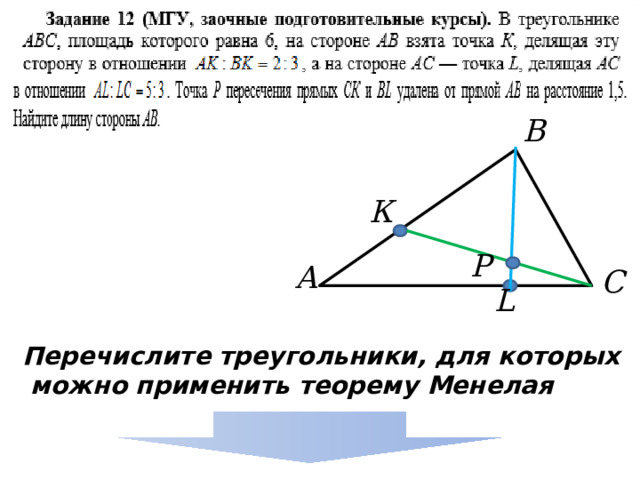
Перечислите треугольники, для которых
можно применить теорему Менелая
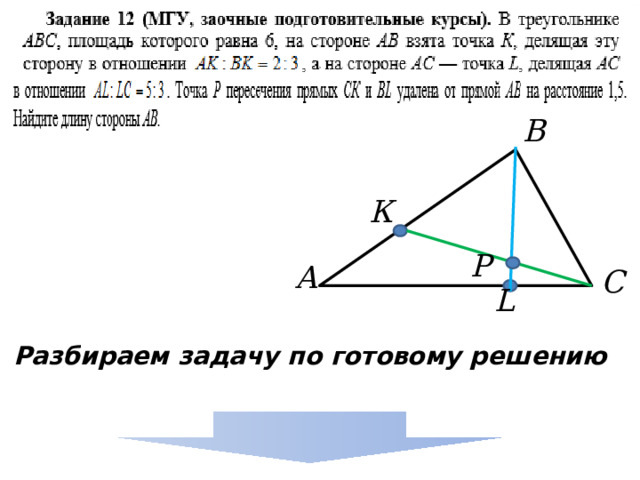
Разбираем задачу по готовому решению


Задание 13. Три окружности с центрами
А, В, С, радиусы которых относятся как
касаются друг друга внешним
образом в точках X, Y, Z как показано на рисунке 19 . Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от точки B, отрезок CZ делит отрезок BY?
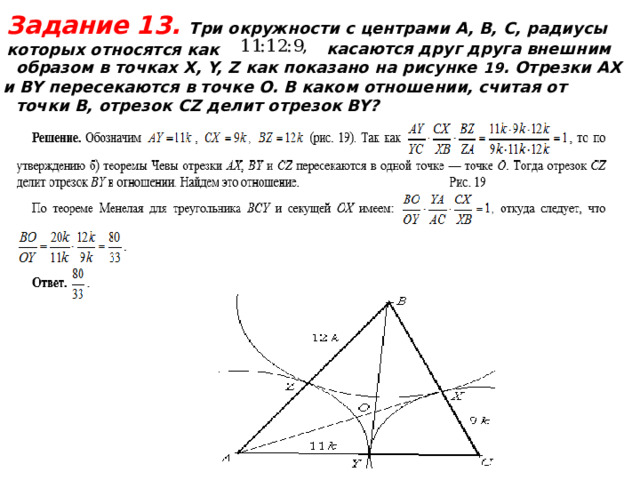
Задание 13. Три окружности с центрами А, В, С, радиусы
которых относятся как
касаются друг друга внешним
образом в точках X, Y, Z как показано на рисунке 19 . Отрезки AX и BY пересекаются в точке O. В каком отношении, считая от
точки B, отрезок CZ делит отрезок BY?


Задание 15 (ЕГЭ-2016).
Точки В 1 и С 1 лежат на сторонах
соответственно АС и АВ треугольника
ABC, причём АВ 1 :B 1 С= АС 1 :С 1 B. Прямые ВВ 1 и СС 1 пересекаются в точке О.
а) Докажите, что прямая АО делит
пополам сторону ВС.
б) Найдите отношение площади
четырёхугольника AB 1 OC 1 к площади
треугольника ABC, если известно, что
АВ 1 : B 1 С = 1:3.
Решить по аналогии с заданием 14
Ответ. 1:10.
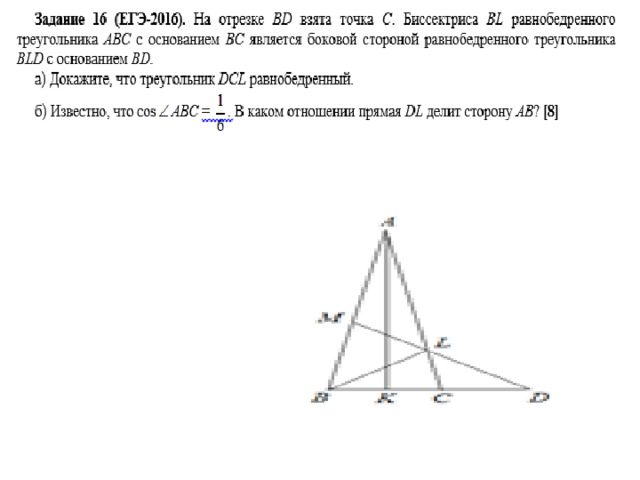


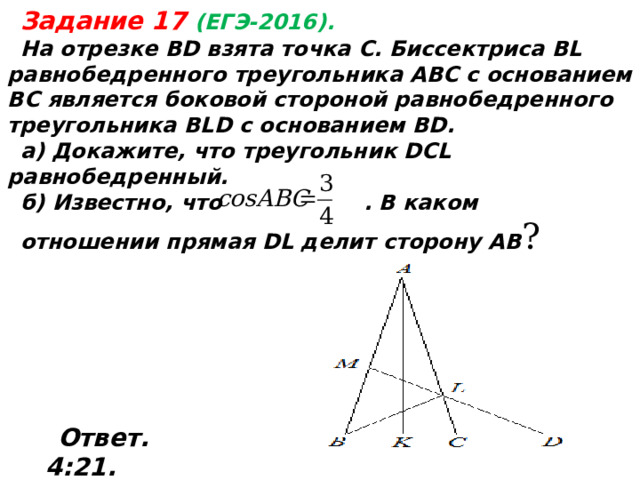
Задание 17 (ЕГЭ-2016).
На отрезке BD взята точка С. Биссектриса BL равнобедренного треугольника ABC с основанием ВС является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) Известно, что . В каком
отношении прямая DL делит сторону АВ ?
Ответ. 4:21 .

Домашняя Работа
1. Теория. Выучить теоремы Чевы и Менелая. Разобрать задачи, решенные в классе.
2.Практика .
Задачи №8,9
на применение теоремы Чевы
Задачи №10,15 на применение теоремы Менелая.
Повторить все формулы площадей
































































