Теория игр. Задача №26 ЕГЭ

Теория Игр

Выигрышные стратегии

Что нужно знать

• в простых играх можно найти выигрышную стратегию, просто перебрав все возможные варианты ходов соперников
• полный перебор вариантов реально выполнить только для очень простых игр; например, в шахматах сделать это за приемлемое время не удается
• все позиции в простых играх делятся на выигрышные и проигрышные

Что нужно знать

• выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, может гарантированно выиграть при любой игре соперника, если не сделает ошибку; при этом говорят, что у него есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть
• если игрок начинает играть в проигрышной позиции, он обязательно проиграет, если ошибку не сделает его соперник; в этом случае говорят, что у него нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для соперника

.

Что нужно знать

• выигрышные и проигрышные позиции можно охарактеризовать так:

• позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная ; позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная , при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию
• позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная ;
• позиция, из которой хотя бы один из возможных ходов ведет в проигрышную позицию - выигрышная , при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную (для соперника) позицию

Задача 1

Задача 1

• Игра состоит в том, что игроки поочередно берут из кучки по одной фишке и выкладывают в цепочку на стол лицевой стороной вверх таким образом, что каждая новая фишка ставится правее предыдущей и ближайшие цифры соседних фишек совпадают.
• Пример. Пусть на столе в кучке лежат фишки: 11, 12, 13, 21, 22, 23
• Пусть первый ход Пети 12. Ваня может поставить 21, 22 или 23. Предположим, он ставит 21. Получим цепочку 12-21. Петя может поставить 11 или 13. Предположим, он ставит 11. Получим цепочку 12-21-11. Ваня может поставить только фишку со значением 13. Получим цепочку 12-21-11-13. Перед Петей в кучке остались только фишки 22 и 23, то есть нет фишек, которые он мог бы добавить в цепочку. Таким образом, партия закончена, Ваня выиграл.

Задача 1

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

• Задание 1.
• а) Приведите пример самой короткой партии, возможной при данном наборе фишек. Если таких партий несколько, достаточно привести одну.
• б) Пусть Петя первым ходом пошел 42. У кого из игроков есть выигрышная стратегия в этой ситуации? Укажите первый ход, который должен сделать выигрывающий игрок, играющий по этой стратегии. Приведите пример одной из партий, возможных при реализации выигрывающим игроком этой стратегии.

Задача 1 (задание 1)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
• а)
• меньше всего фишек заданного набора начинается с цифры 1 (только 12 и 14), поэтому самой короткой партией, вероятно, будет партия, которая заканчивается на цифре 1 (фишкой 21 или 41), при этом фишки 12 и 14 должны быть выставлены;

12 – 21 – 14 – 41 и 14 – 41 – 12 – 21

• В ответе достаточно привести одну из них.

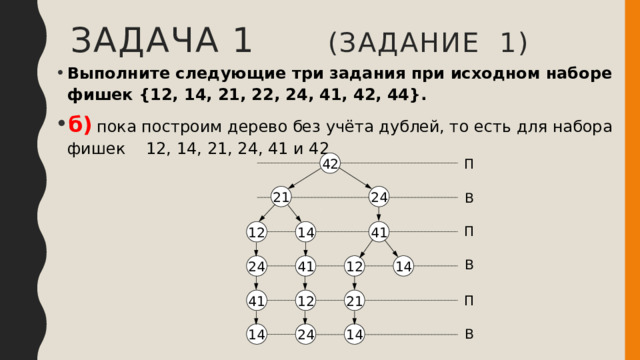
Задача 1 (задание 1)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.
• б) пока построим дерево без учёта дублей, то есть для набора фишек 12, 14, 21, 24, 41 и 42

42

П

21

24

В

П

41

12

14

В

24

41

12

14

П

12

41

21

В

14

24

14

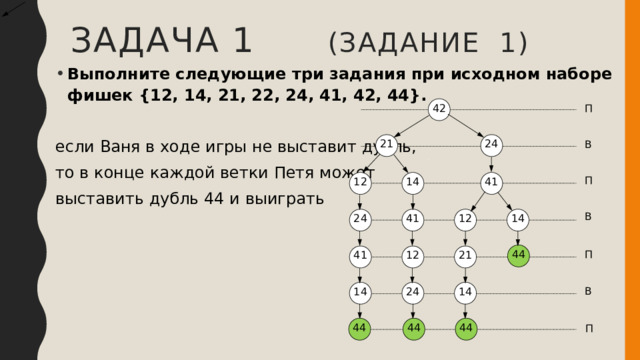
Задача 1 (задание 1)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

если Ваня в ходе игры не выставит дубль,

то в конце каждой ветки Петя может

выставить дубль 44 и выиграть

П

42

21

24

В

П

41

14

12

В

41

24

12

14

44

П

21

41

12

В

14

14

24

44

44

44

П

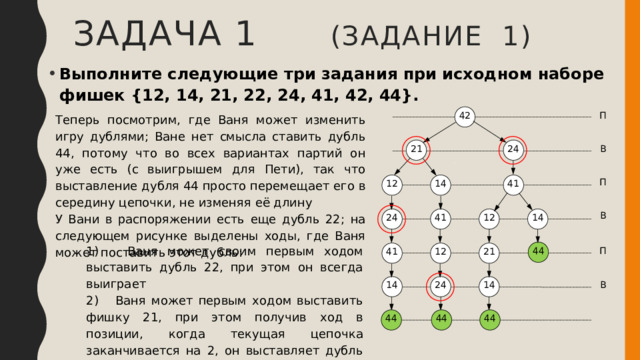
Задача 1 (задание 1)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

42

П

Теперь посмотрим, где Ваня может изменить игру дублями; Ване нет смысла ставить дубль 44, потому что во всех вариантах партий он уже есть (с выигрышем для Пети), так что выставление дубля 44 просто перемещает его в середину цепочки, не изменяя её длину

У Вани в распоряжении есть еще дубль 22; на следующем рисунке выделены ходы, где Ваня может поставить этот дубль:

21

24

В

П

14

12

41

В

24

14

12

41

1) Ваня может своим первым ходом выставить дубль 22, при этом он всегда выиграет

2) Ваня может первым ходом выставить фишку 21, при этом получив ход в позиции, когда текущая цепочка заканчивается на 2, он выставляет дубль 22 и выигрывает

44

П

41

21

12

В

14

24

14

44

44

44

Задача 1 (задание 2)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

• Задание 2
• Пусть Петя первым ходом пошел 44. У кого из игроков есть выигрышная стратегия, позволяющая в этой ситуации выиграть своим четвертым ходом? Постройте в виде рисунка или таблицы дерево всех партий, возможных при реализации выигрывающим игроком этой стратегии. На рёбрах дерева указывайте ход, в узлах – цепочку фишек, получившуюся после этого хода.

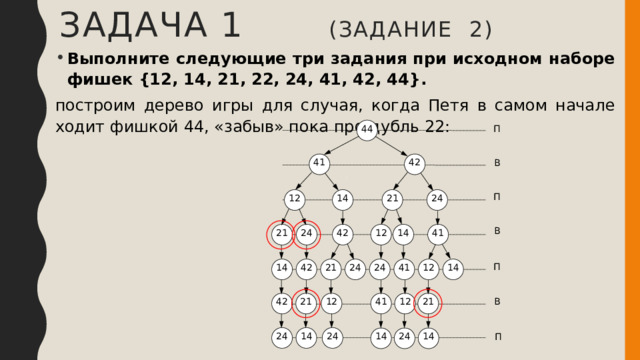
Задача 1 (задание 2)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

построим дерево игры для случая, когда Петя в самом начале ходит фишкой 44, «забыв» пока про дубль 22:

П

44

41

42

В

П

21

12

14

24

В

12

41

42

14

21

24

П

24

42

14

24

21

14

12

41

В

42

21

12

41

21

12

14

24

24

14

24

14

П

Задача 1 (задание 2)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

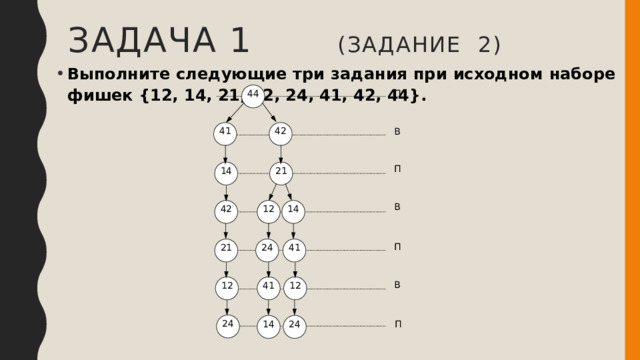
• по дереву видим, что при игре без дубля 22 выигрывает Петя своим третьим или четвёртым ходом
• Ваня может изменить ход игры дублем 22 только в выделенных узлах, поэтому

• если Ваня походит фишкой 41, Петя должен ответить ходом 14

• если Ваня походит фишкой 42, Петя должен ответить ходом 21

Задача 1 (задание 2)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

44

П

41

42

В

П

14

21

В

14

42

12

П

21

41

24

В

12

12

41

24

24

14

П

Задача 1

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

• Задание 3
• Укажите хотя бы один способ убрать 2 фишки из исходного набора так, чтобы всегда выигрывал не тот игрок, который имеет выигрышную стратегию в задании 2. Приведите пример партии для набора из 6 оставшихся фишек.

Задача 1 (задание 3)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

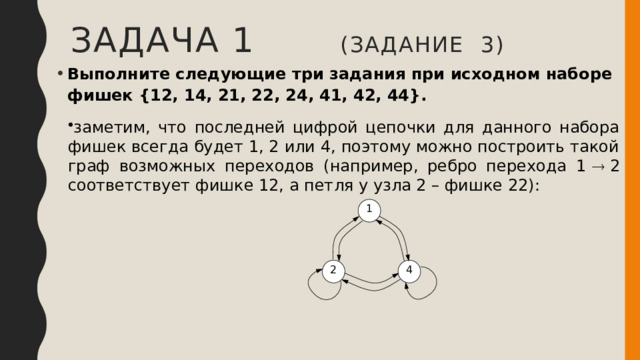
• заметим, что последней цифрой цепочки для данного набора фишек всегда будет 1, 2 или 4, поэтому можно построить такой граф возможных переходов (например, ребро перехода 1     2 соответствует фишке 12, а петля у узла 2 – фишке 22):

1

2

4

Задача 1 (задание 3)

• Выполните следующие три задания при исходном наборе фишек {12, 14, 21, 22, 24, 41, 42, 44}.

если убрать два дубля, то всегда будут выставлены 4 или все 6 фишек, поскольку 4 и 6 – чётные числа, то всегда выиграет Ваня, потому что он делает все ходы с чётными номерами; например, при первом ходе Пети 12 возможны партии:

12 – 21 – 14 – 41 или 12 – 24 – 41 – 14 – 42 – 21.

Задача 2

Задача 2

• Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
• а) добавить в кучу один камень или
• б) увеличить количество камней в куче в два раза .
• Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Если при этом в куче оказалось не более 38 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче был 21 камень и Петя удвоит количество камней в куче, то игра закончится и победителем будет Ваня. В начальный момент в куче было S камней, 1

Задача 2

• Задание 1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.
• б) У кого из игроков есть выигрышная стратегия при S = 22, 21, 20? Опишите выигрышные стратегии для этих случаев.
• Задание 2 . У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
• Задание 3 . У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.

Задача 2 (задание 1)

• а)
• Сложность состоит в том, что Петя проиграет, если в результате его хода количество камней станет больше, чем 38. Он может сделать ход «+1» или «*2». Ходом «+1» он сможет получить 24 камня в куче (и таким образом выиграет!) из позиции S = 23.

• Теперь проверим ход «*2». Для выигрыша Пети количество камней в результате этого хода должно стать от 24 до 38, поэтому Петя выиграет этим ходом при S от 12 до 19.

38. Поэтому позиция S = 22 – проигрышная, Петя проиграет, у Вани есть выигрышная стратегия: в случае S = 23 сделать ход «+1» . При S = 21 Петя может перевести игру в позицию S = 22, она, как мы только что показали, проигрышная для Вани. Поэтому у Пети есть выигрышная стратегия. При S = 20 ходом «+1» Петя переведет игру в выигрышную (для Вани) позицию, а при ходе «*3» он сразу проиграет, получив 40 38 камней. Поэтому выигрышная стратегия есть у Вани. " width="640"

Задача 2 (задание 1)

• б)
• При S = 22 возможные ходы дают кучи в 23 и 44 камня. В первом случае (S = 23) противник оказывается в выигрышной позиции (см. предыдущий пункт), во втором случае тот, кто ходит, проигрывает, потому что 44 38. Поэтому позиция S = 22 – проигрышная, Петя проиграет, у Вани есть выигрышная стратегия: в случае S = 23 сделать ход «+1» .
• При S = 21 Петя может перевести игру в позицию S = 22, она, как мы только что показали, проигрышная для Вани. Поэтому у Пети есть выигрышная стратегия.
• При S = 20 ходом «+1» Петя переведет игру в выигрышную (для Вани) позицию, а при ходе «*3» он сразу проиграет, получив 40 38 камней. Поэтому выигрышная стратегия есть у Вани.

Задача 2 (задание 2)

• При S = 11 или S = 10 Петя может ходом «*2» перевести игру в позиции S = 22 и S = 20, обе они, как мы показали в предыдущем пункте, проигрышные. Поэтому выигрышную стратегию имеет Петя.

Задача 2 (задание 3)

• При S = 9 возможно 2 хода: ход «+1» приводит к позиции S = 10, она выигрышная (см. предыдущий пункт); ход «*2» приводит к позиции S = 18, она тоже выигрышная (см. первый пункт). Таким образом, все возможные ходы ведут в выигрышные для соперника позиции, и позиция S = 9 – проигрышная (для Пети). Выигрышную стратегию имеет Ваня.

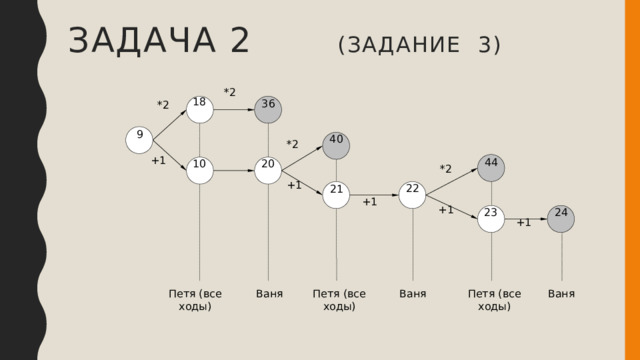
Задача 2 (задание 3)

*2

18

36

*2

9

40

*2

+1

44

10

20

*2

+1

22

21

+1

+1

23

24

+1

Петя (все ходы)

Петя (все ходы)

Петя (все ходы)

Ваня

Ваня

Ваня

Задача 2 (задание 3)

или записать в виде таблицы

 

Петя

9

Ваня

9*2=18

9+1=10

Петя

18*2=36

Ваня

 

10*2=20

Петя

20*2=40

 

 

Ваня

 

20+1=21

 

 

21+1=22

 

22+1=23

22*2=44

23+1=24