При решении этих задач сначала нужно определить, в чем состоит случайный эксперимент, какие у него элементарные исходы и убедиться, что они равновозможны.
Далее следует найти общее число элементарных событий 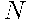 .
.
Теперь нужно определить, какие элементарные события благоприятствуют интересующему нас событию  , и найти их число
, и найти их число 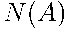 .
.
Вероятность события найдём по формуле 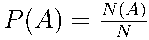 .
.
Задача 1.
Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдитевероятность того, что начинать игру должен будет Петя.
Решение.
Случайный эксперимент — бросание жребия.
В этом эксперименте элементарным событием является участник, который выиграл жребий.
Перечислим возможные элементарные события:
(Вася), (Петя), (Коля), (Лёша).
Их будет будет 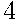 , т.е.
, т.е. 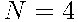 .
.
Жребий подразумевает, что все элементарные события равновозможны.
Событию  = {жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому
= {жребий выиграл Петя} благоприятствует только одно элементарное событие (Петя). Поэтому 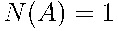 .
.
Тогда 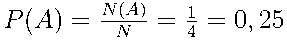 .
.
Ответ: 0,25.
Задача 2.
Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, большее чем 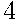 ?
?
Решение.
В этой задаче случайным экспериментом является бросание кубика. Элементарным исходом является число на выпавшей грани. Граней всего шесть.
Можно перечислить все элементарные исходы:
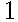 ,
, 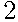 ,
, 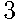 ,
, 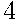 ,
, 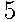 и
и 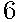 .
.
Следовательно, 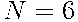 .
.
Событию  = {выпало больше чем 4} благоприятствуют два элементарных исхода:
= {выпало больше чем 4} благоприятствуют два элементарных исхода: 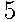 и
и 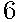 . Поэтому
. Поэтому 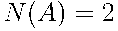 .
.
Подразумевается, что кубик честный, следовательно, все элементарные события равновозможны. Поэтому 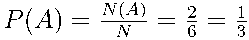
Ответ: 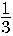 .
.
Задача 3.
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Обозначим буквой О выпадение орла, а выпадение решки буквой Р. В приведённом эксперименте могут быть следующие элементарные исходы:
ОО, ОР, РО и РР.
Всего исходов 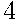 , поэтому
, поэтому 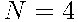 .
.
Событию  = {выпал ровно один орел} благоприятствуют
= {выпал ровно один орел} благоприятствуют 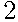 элементарных события ОР и РО, следовательно,
элементарных события ОР и РО, следовательно, 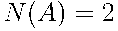 .
.
Теперь можно найти вероятность того, что орёл выпадет ровно один раз 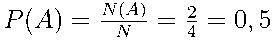 .
.
Ответ: 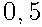 .
.
Задача 4.
В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 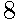 очков.
очков.
Решение.
Элементарным исходом в этом опыте является упорядоченная пара чисел. Первое число выпадает на первом кубике, а второе — на втором. В таких задачах множество элементарных исходов удобно представить в виде таблицы. В первой строке этой таблицы записываем возможный результат первого броска, а в первом столбце - возможный результат второго броска. Количество элементарных исходов 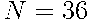 .
.
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1;1) | (2;1) | (3;1) | (4;1) | (5;1) | (6;1) |
| 2 | (1;2) | (2;2) | (3;2) | (4;2) | (5;2) | (6;2) |
| 3 | (1;3) | (2;3) | (3;3) | (4;3) | (5;3) | (6;3) |
| 4 | (1;4) | (2;4) | (3;4) | (4;4) | (5;4) | (6;4) |
| 5 | (1;5) | (2;5) | (3;5) | (4;5) | (5;5) | (6;5) |
| 6 | (1;6) | (2;6) | (3;6) | (4;6) | (5;6) | (6;6) |
Напишем в каждой клетке таблицы элементарные исходы и закрасим клетки, где сумма равна 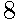 (см. рис.). Таких клеток будет пять. Значит, событию
(см. рис.). Таких клеток будет пять. Значит, событию  = {сумма равна
= {сумма равна 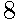 } благоприятствуют
} благоприятствуют 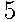 элементарных исходов, а, следовательно,
элементарных исходов, а, следовательно, 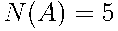 . Поэтому вероятность того, что в сумме выпадет
. Поэтому вероятность того, что в сумме выпадет 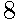 очков, можно найти по формуле
очков, можно найти по формуле 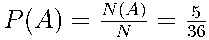 .
.
Ответ: 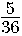 .
.
Задача 5.
В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
Решение.
Обозначим буквой О выпадение орла, а буквой Р – выпадение решки. Элементарными исходами в данной задаче являются всевозможные тройки, составленные из букв О и Р. Запишем их все в таблицу:
| Элементарный исход | Число орлов |
| ООО | 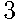 |
| ООР | 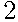 |
| ОРО | 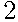 |
| ОРР | 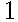 |
| РОО | 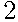 |
| РОР | 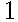 |
| РРО | 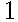 |
| РРР | 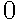 |
Всего разных исходов получилось 8. Значит, 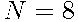 .
.
Событию  = {орел выпал ровно два раза} благоприятствуют элементарные события ООР, ОРО и РОО (они выделены в таблице зелёным цветом),поэтому
= {орел выпал ровно два раза} благоприятствуют элементарные события ООР, ОРО и РОО (они выделены в таблице зелёным цветом),поэтому 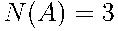 .
.
Тогда 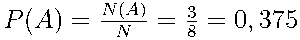
Ответ: 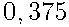 .
.
Задача 6.
В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение.
В этой задаче элементарным исходом является спортсмен, который выступает последним. Последним может оказаться любой. Всего спортсменов 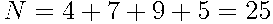 .
.
Событию  = {последний из Швеции} благоприятствуют только
= {последний из Швеции} благоприятствуют только 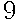 исходов (это число спортсменов из Швеции). Следовательно,
исходов (это число спортсменов из Швеции). Следовательно, 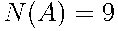 .
.
Вероятность того, что спортсмен, выступающий последним, будет из Швеции, найдём по формуле 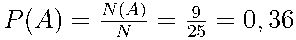 .
.
Ответ: 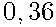
Задача 7.
В среднем из 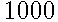 аккумуляторов, поступивших в продажу,
аккумуляторов, поступивших в продажу, 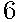 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Решение.
1 способ.
Элементарным исходом в этой задаче является случайно выбранный аккумулятор. Всего аккумуляторов 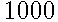 , поэтому
, поэтому 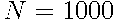 .
.
Событию  = {аккумулятор исправен} благоприятствуют 994 исхода, поскольку исправных аккумуляторов
= {аккумулятор исправен} благоприятствуют 994 исхода, поскольку исправных аккумуляторов 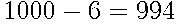 . Следовательно,
. Следовательно, 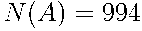 .
.
Тогда 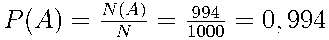 .
.
2 способ.
Эту задачу можно решить с помощью формулы вероятности противоположного события 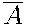 = {аккумулятор неисправен}. Имеем
= {аккумулятор неисправен}. Имеем 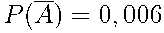 .
.
Значит, 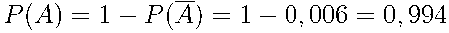 .
.
Ответ: 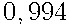 .
.
Задача 8
В чемпионате по гимнастике участвуют 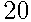 спортсменок:
спортсменок: 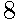 из России,
из России, 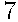 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
Элементарное событие — спортсменка, выступающая первой. По условию задачи все элементарные события равновозможны, поэтому 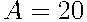 .
.
Чтобы найти число элементарных событий, благоприятствующих событию  = {первой выступает спортсменка из Китая}, подсчитаем число спортсменок из Китая:
= {первой выступает спортсменка из Китая}, подсчитаем число спортсменок из Китая:
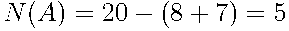 .
.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая найдём по формуле 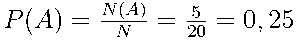 .
.
Ответ: 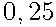 .
.
Задача 9
В чемпионате мира участвуют 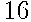 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
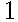 ,
, 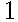 ,
, 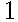 ,
, 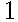 ,
, 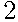 ,
, 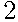 ,
, 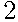 ,
, 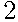 ,
, 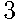 ,
, 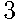 ,
, 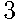 ,
, 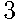 ,
, 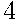 ,
, 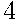 ,
, 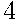 ,
, 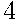 .
.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение.
Пусть элементарный исход — это карточка, выбранная капитаном российской команды. Поскольку карточек 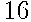 , то
, то 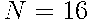 . Событию
. Событию  = {команда России во второй группе} благоприятствуют четыре карточки с номером
= {команда России во второй группе} благоприятствуют четыре карточки с номером 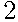 , то есть
, то есть 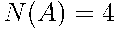 .
.
Тогда 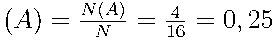 .
.
Ответ: 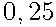 .
.
Элементарные события (элементарные исходы) опыта — простейшие события, которыми может окончиться случайный опыт.
Сумма вероятностей всех элементарных событий опыта равна 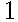 .
.
Вероятность события  равна сумме вероятностей элементарных событий, благоприятствующих этому событию.
равна сумме вероятностей элементарных событий, благоприятствующих этому событию.
Объединение событий 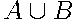 — событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий
— событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий  ,
, 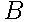 .
.
Пересечение событий  — событие, состоящие из элементарных исходов, благоприятствующих обоим событиям
— событие, состоящие из элементарных исходов, благоприятствующих обоим событиям  и
и 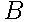 .
.
Противоположное событие.
Событие 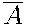 , состоящее из тех и только тех элементарных исходов опыта, которые не входят в
, состоящее из тех и только тех элементарных исходов опыта, которые не входят в  , называется противоположным событию
, называется противоположным событию  .
.
Несовместные события — события, которые не наступают в одном опыте. Например, противоположные события несовместны.
Вероятности противоположных событий:
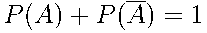 ;
; 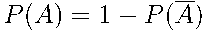 .
.
Формула сложения вероятностей:
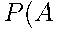 и
и 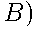 =
= 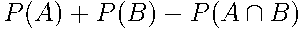 .
.
Формула сложения вероятностей для несовместных событий:
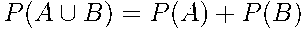 .
.
Задача 1.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 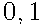 . Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
. Покупатель в магазине выбирает одну такую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Решение.
Определим событие  = {выбранная ручка пишет хорошо}.
= {выбранная ручка пишет хорошо}.
Тогда противоположное событие 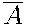 = {выбранная ручка пишет плохо}.
= {выбранная ручка пишет плохо}.
Из условия нам известна вероятность противоположного события: 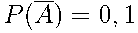 .
.
Используем формулу вероятности противоположного события:
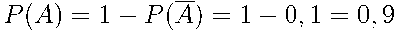 .
.
Ответ: 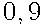 .
.
Задача 2.
На экзамене по геометрии школьнику достается один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 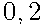 . Вероятность того, что это вопрос на тему «Параллелограмм», равна
. Вероятность того, что это вопрос на тему «Параллелограмм», равна 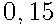 . Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Определим события:
 = {вопрос на тему «Вписанная окружность»},
= {вопрос на тему «Вписанная окружность»},
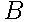 = {вопрос на тему «Параллелограмм»}.
= {вопрос на тему «Параллелограмм»}.
События  и
и 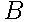 несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.
несовместны, так как по условию в списке нет вопросов, относящихся к этим двум темам одновременно.
Событие  = {вопрос по одной из этих двух тем} является их объединением:
= {вопрос по одной из этих двух тем} является их объединением: 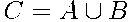 .
.
Применим формулу сложения вероятностей несовместных событий:
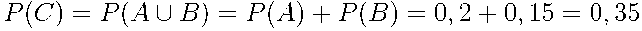 .Ответ:
.Ответ: 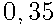 .
.
Задача 3.
В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 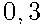 . Вероятность того, что кофе закончится в обоих автоматах, равна
. Вероятность того, что кофе закончится в обоих автоматах, равна 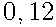 . Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.
Решение.
Определим события
 = {кофе закончится в первом автомате},
= {кофе закончится в первом автомате},
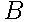 = {кофе закончится во втором автомате}.
= {кофе закончится во втором автомате}.
По условию задачи 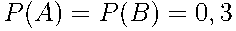 и
и 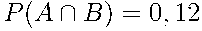 .
.
По формуле сложения вероятностей найдем вероятность события
 и
и 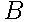 = {кофе закончится хотя бы в одном из автоматов}:
= {кофе закончится хотя бы в одном из автоматов}:
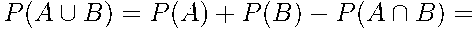
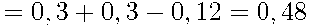 .
.
Следовательно, вероятность противоположного события {кофе останется в обоих автоматах} равна
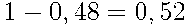 .
.
Ответ: 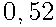 .
.
Задача 4.
Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 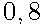 . Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение.
В этой задаче предполагается, что результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна 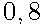 . Значит, вероятность каждого промаха равна
. Значит, вероятность каждого промаха равна 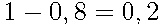 . Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что последовательность
. Воспользуемся формулой умножения вероятностей независимых событий. Получаем, что последовательность
 = {попал, попал, попал, промахнулся, промахнулся} имеет вероятность
= {попал, попал, попал, промахнулся, промахнулся} имеет вероятность
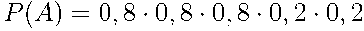 =
=
= 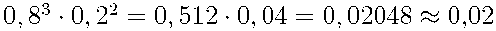 .
.
Ответ: 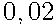 .
.
Задача 5.
В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 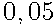 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение.
В этой задаче также предполагается независимость работы автоматов.
Найдем вероятность противоположного события
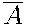 = {оба автомата неисправны}.
= {оба автомата неисправны}.
Для этого используем формулу умножения вероятностей независимых событий:
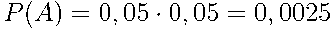 .
.
Значит, вероятность события  = {хотя бы один автомат исправен} равна
= {хотя бы один автомат исправен} равна 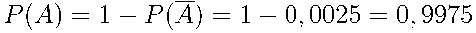 .
.
Ответ: 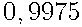 .
.
В следующих задачах для решения удобно использовать дерево вероятностей. В части задач дерево построено прямо в условии. В других задачах это дерево следует построить. Попробуйте решить с помощью дерева вероятностей также некоторые из предыдущих задач, например, задачи 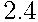 и
и 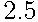 .
.
Задача 1.
Павел Иванович совершает прогулку из точки  по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.
по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно.
Схема дорожек показана на рисунке. Найдите вероятность того, что Павел Иванович попадет в точку  .
.
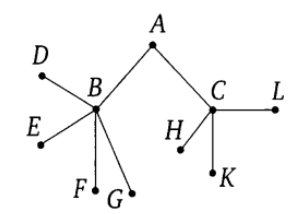
Решение.
Схема дорожек представляет собой граф, а именно — дерево. Рёбра (ветви) дерева соответствуют дорожкам. Около каждого ребра напишем вероятность того, что Павел Иванович пройдет по соответствующей дорожке. Выбор пути на каждой развилке происходит наудачу, поэтому вероятность поровну делится между всеми возможностями. Предположим, что Павел Иванович пришел в вершину  . Из неё выходит три ребра
. Из неё выходит три ребра 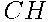 ,
, 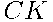 и
и 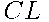 .Следовательно, вероятность того, что Павел Иванович выберет ребро
.Следовательно, вероятность того, что Павел Иванович выберет ребро 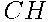 , равна
, равна 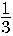 . Аналогично можно расставить все вероятности.
. Аналогично можно расставить все вероятности.
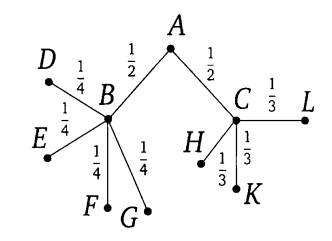
Каждый маршрут из начальной точки  в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.
в любую из конечных точек является элементарным событием в этом эксперименте. События здесь не равновозможные. Вероятность каждого элементарного события можно найти по правилу умножения.
Нам нужно найти вероятность элементарного события
 = {Павел Иванович пришел в точку
= {Павел Иванович пришел в точку  }.
}.
Это событие состоит в том, что Павел Иванович прошел маршрутом 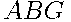 . Вероятность находится умножением вероятностей вдоль ребер
. Вероятность находится умножением вероятностей вдоль ребер 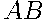 и
и  :
: 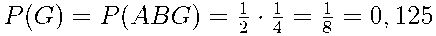 .
.
Ответ: 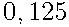 .
.
Задача 2.
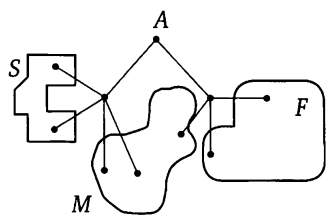
Павел Иванович совершает прогулку из точки А по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку 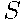 , другие — в поле
, другие — в поле 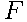 или в болото
или в болото 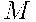 . Найдите вероятность того, что Павел Иванович забредет в болото.
. Найдите вероятность того, что Павел Иванович забредет в болото.
Решение.
В болото ведут три маршрута. Обозначим вершины на этих маршрутах и напишем на ребрах вдоль этих маршрутов соответствующие вероятности. Остальные маршруты не будем рассматривать.
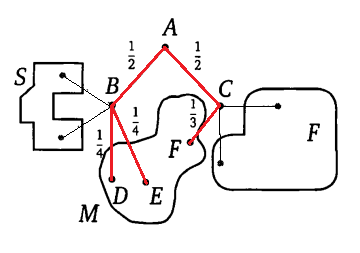
Вероятность события {Павел Иванович попадет в болото}, равна 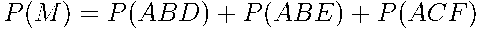 =
=
= 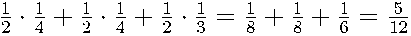 .
.
Ответ: 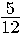
Задача 3.
В некотором эксперименте вероятность события  равна
равна 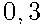 . Если событие
. Если событие  наступает, то вероятность события
наступает, то вероятность события  равна
равна 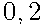 , а в противоположном случае вероятность события
, а в противоположном случае вероятность события  равна
равна 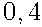 . Найдите вероятность события
. Найдите вероятность события  .
.
Решение.
В таких задачах удобно изобразить эксперимент графически деревом вероятностей. Отличие от предыдущих задач состоит в том, что вероятности на ребрах получаются не из равновозможности, а иначе.
Весь эксперимент обозначим буквой 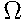 (большая омега) и поставим точку около этой буквы — корень дерева, из которого ветви-ребра растут вниз. Из точки
(большая омега) и поставим точку около этой буквы — корень дерева, из которого ветви-ребра растут вниз. Из точки 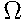 проведем ребро вниз-влево в точку
проведем ребро вниз-влево в точку  . Событие
. Событие  имеет вероятность
имеет вероятность 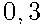 , поэтому подпишем у этого ребра вероятность
, поэтому подпишем у этого ребра вероятность 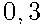 . Противоположное событие А имеет вероятность
. Противоположное событие А имеет вероятность 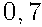 . Проведем второе ребро в точку
. Проведем второе ребро в точку  .
.
Если осуществилось событие  , то событие
, то событие  по условию имеет вероятность
по условию имеет вероятность 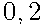 . Поэтому из точки
. Поэтому из точки  проведем ребро вниз-влево в точку
проведем ребро вниз-влево в точку  и подпишем вероятность. Действуя так же и дальше, достроим все дерево (см. рис.).
и подпишем вероятность. Действуя так же и дальше, достроим все дерево (см. рис.).
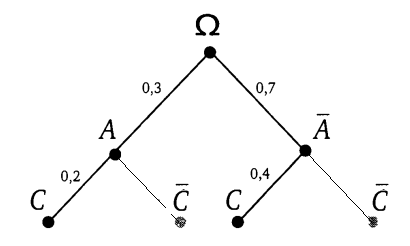
Чтобы найти вероятность события  , нужно выделить только те пути, которые ведут из корневой точки
, нужно выделить только те пути, которые ведут из корневой точки 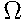 к событию
к событию  . На рисунке эти пути яркие, а пути, не приводящие к
. На рисунке эти пути яркие, а пути, не приводящие к  изображены бледно. Выделенные пути
изображены бледно. Выделенные пути 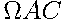 и
и 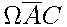 являются элементарными событиями, благоприятствующими событию
являются элементарными событиями, благоприятствующими событию  .
.
Теперь нужно вычислить вероятности выделенных путей и сложить их. Пользуясь правилами умножения и сложения вероятностей, получаем:
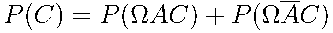 =
=
= 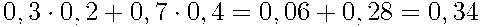 .
.
Ответ: 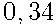
Задача 4.
Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 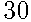 % всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой,
% всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 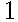 % имеют скрытые дефекты, а у выпускаемых второй фабрикой —
% имеют скрытые дефекты, а у выпускаемых второй фабрикой — 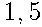 %. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
%. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Решение.
Введем обозначения для событий:
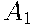 = {телефон выпущен на первой фабрике},
= {телефон выпущен на первой фабрике},
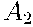 = {телефон выпущен на второй фабрике},
= {телефон выпущен на второй фабрике},
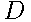 = {телефон имеет скрытый дефект}.
= {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.
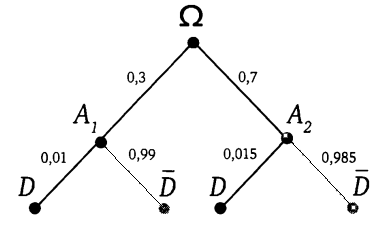
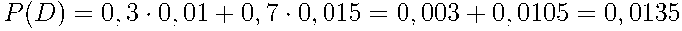 .
.
Ответ: 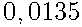
Задача 4.
Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 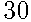 % всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой,
% всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 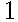 % имеют скрытые дефекты, а у выпускаемых второй фабрикой —
% имеют скрытые дефекты, а у выпускаемых второй фабрикой — 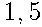 %. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
%. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.
Решение.
Введем обозначения для событий:
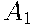 = {телефон выпущен на первой фабрике},
= {телефон выпущен на первой фабрике},
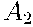 = {телефон выпущен на второй фабрике},
= {телефон выпущен на второй фабрике},
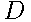 = {телефон имеет скрытый дефект}.
= {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.

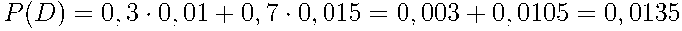 .Ответ:
.Ответ: