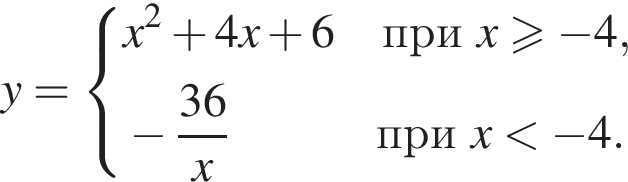На рисунке изображен план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка.
Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора — дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застекленных лоджий. Самое большое по площади помещение — гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застекленную лоджию.
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырех цифр без пробелов, запятых и других дополнительных символов.
| Объекты | коридор | кладовая | спальня | гостиная |
| Цифры |
|
|
|
|
2. Плитка для пола размером 40 см на 40 см продается в упаковках по 12 штук. Сколько упаковок плитки понадобится, чтобы выложить пол санузла?
3. Найдите площадь санузла. Ответ дайте в квадратных метрах.
4. На сколько процентов площадь коридора больше площади кладовой?
5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6 кг.
| Модель | Вместимость барабана (кг) | Тип загрузки | Стоимость (руб.) | Стоимость подключения (руб.) | Стоимость доставки (% от стоимости машины) | Габариты (высота × ширина × глубина, см) |
| А | 7 | верт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Б | 5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 40 |
| В | 5 | фронт. | 25 000 | 5000 | 10 | 85 × 60 × 40 |
| Г | 6,5 | фронт. | 24 000 | 4500 | 10 | 85 × 60 × 44 |
| Д | 6 | фронт. | 28 000 | 1700 | бесплатно | 85 × 60 × 45 |
| Е | 6 | верт. | 27 600 | 2300 | бесплатно | 89 × 60 × 40 |
| Ж | 6 | верт. | 27 585 | 1900 | 10 | 89 × 60 × 40 |
| З | 6 | фронт. | 20 000 | 6300 | 15 | 85 × 60 × 42 |
| И | 5 | фронт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
| К | 5 | верт. | 27 000 | 1800 | бесплатно | 85 × 60 × 40 |
Сколько рублей будет стоить наиболее дешевый подходящий вариант вместе с подключением и доставкой?
6. Найдите значение выражения 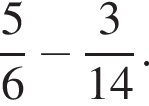 Представьте результат в виде несократимой обыкновенной дроби. В ответ запишите числитель этой дроби.
Представьте результат в виде несократимой обыкновенной дроби. В ответ запишите числитель этой дроби.
7. Известно, что 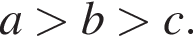 Какое из следующих чисел отрицательно?
Какое из следующих чисел отрицательно?
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4) 
8.
Найдите значение выражения 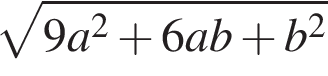 при
при 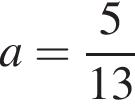 и
и 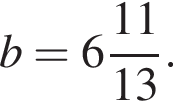
9. Решите уравнение 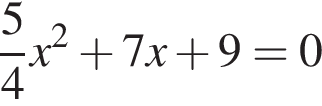
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
10. Валя выбирает случайное трехзначное число. Найдите вероятность того, что оно делится на 51.
11. На рисунке изображен график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведенную в ответе таблицу под каждой буквой соответствующую цифру.
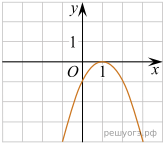
| УТВЕРЖДЕНИЯ | | ПРОМЕЖУТКИ |
| А) функция возрастает на промежутке Б) функция убывает на промежутке | | 1) [1; 2] 2) [0; 2] 3) [−1; 0] 4) [−2; 3] |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
12. Центростремительное ускорение (в м/c2) вычисляется по формуле α = ω2R, где ω — угловая скорость (в с–1), R — радиус окружности. Пользуясь этой формулой, найдите радиус R (в метрах), если угловая скорость равна 5 с–1, а центростремительное ускорение равно 35 м/c2.
13. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1) 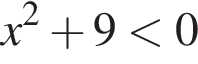
2) 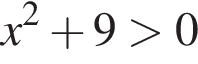
3) 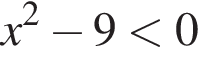
4) 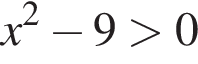
14. Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.
15.  Прямые m и n параллельны. Найдите ∠3, если ∠1 = 117°, ∠2 = 24°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 117°, ∠2 = 24°. Ответ дайте в градусах.
16.  AC и BD — диаметры окружности с центром O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах.
17. 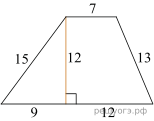 Найдите площадь трапеции, изображенной на рисунке.
Найдите площадь трапеции, изображенной на рисунке.
18.  Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображенного на рисунке.
19. Какие из следующих утверждений верны?
1) Если площади фигур равны, то равны и сами фигуры.
2) Площадь трапеции равна произведению суммы оснований на высоту.
3) Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.
4) Если две смежные стороны параллелограмма равны 4 и 5, а угол между ними равен 30°, то площадь этого параллелограмма равна 10.
Если утверждений несколько, запишите их номера в порядке возрастания.
20. Решите уравнение 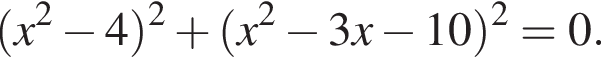
21. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 112 км. На следующий день он отправился обратно в город А, увеличив скорость на 9 км/ч. По пути он сделал остановку на 4 часа, в результате чего затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
22. Постройте график функции
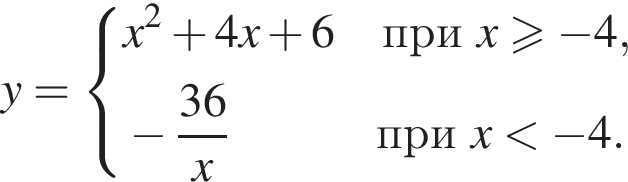
Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.
23. Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
24. Сторона AB параллелограмма ABCD вдвое больше стороны BC. Точка L — середина стороны AB. Докажите, что CL — биссектриса угла BCD.
25. Основание AC равнобедренного треугольника ABC равно 16. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Ключ
| № п/п | № задания | Ответ |
| 1 | 400935 | 2346 |
| 2 | 409278 | 3 |
| 3 | 409292 | 4,8 |
| 4 | 409300 | 525 |
| 5 | 409311 | 29700 |
| 6 | 439897 | 13 |
| 7 | 311305 | 4 |
| 8 | 412196 | 8 |
| 9 | 353555 | -3,6-2 |
| 10 | 325460 | 0,02 |
| 11 | 333008 | 31 |
| 12 | 350660 | 1,4 |
| 13 | 314604 | 3 |
| 14 | 393952 | 30 |
| 15 | 350179 | 39 |
| 16 | 349866 | 24 |
| 17 | 39 | 168 |
| 18 | 40 | 2 |
| 19 | 169936 | 4 |
| 20 | 338237 | −2. |
| 21 | 392961 | 12 км/ч. |
| 22 | 392700 | 
|
| 23 | 311572 | 14,5. |
| 24 | 314944 | 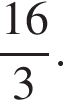
|









 Прямые m и n параллельны. Найдите ∠3, если ∠1 = 117°, ∠2 = 24°. Ответ дайте в градусах.
Прямые m и n параллельны. Найдите ∠3, если ∠1 = 117°, ∠2 = 24°. Ответ дайте в градусах. AC и BD — диаметры окружности с центром O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах.
AC и BD — диаметры окружности с центром O. Угол ACB равен 78°. Найдите угол AOD. Ответ дайте в градусах. Найдите площадь трапеции, изображенной на рисунке.
Найдите площадь трапеции, изображенной на рисунке. Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображенного на рисунке.