Тест двугранный угол

Вариант 1

Вариант 2

Использован шаблон создания тестов в PowerPoint

Результат теста

Верно: 14

Ошибки: 0

Отметка: 5

исправить

Время: 2 мин. 3 сек.

ещё

Вариант 1

1. Линейным углом двугранного угла нельзя назвать угол, возникающий при пересечении двугранного угла плоскостью, перпендикулярной…..

а) ребру двугранного угла

б) одной из граней двугранного угла

в) граням двугранного угла

Вариант 1

2. Какое утверждение верное ?

а) Не может ребро двугранного угла быть не перпендикулярным плоскости его линейного угла.

б) Не могут две плоскости, перпендикулярные к одной плоскости, быть не параллельными.

в) Не могут две плоскости, перпендикулярные к одной прямой , быть параллельными.

Вариант 1

3. Какое утверждение верное ?

а) если α┴ ẞ , а принадлежит α , b принадлежит ẞ , то а ┴b

б) если α∩ ẞ =с, α┴ ẞ , а принадлежит α , b принадлежит ẞ и b┴c то а ┴b

в) если а принадлежит α , b принадлежит ẞ , а ┴b то α┴ ẞ

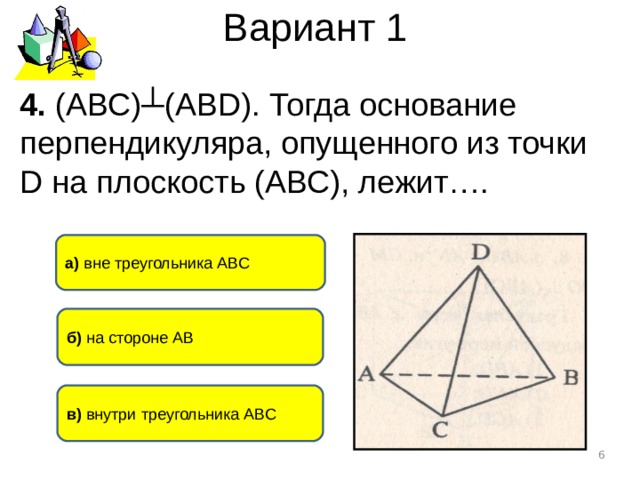
Вариант 1

4. (АВС)┴(АВ D ). Тогда основание перпендикуляра, опущенного из точки D на плоскость (АВС ) , лежит….

а) вне треугольника АВС

б) на стороне АВ

в) внутри треугольника АВС

Вариант 1

5. Какое утверждение неверное ?

а) Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

б) Если плоскости перпендикулярны, то линии их пересечения перпендикулярна любой прямой, лежащей в одной из данных плоскостей.

в) Плоскость, перпендикулярная линии пересечения двух данных плоскостей, перпендикулярна к каждой из этих плоскостей.

Вариант 1

6. Не может плоскость быть не перпендикулярной данной плоскости, если она проходит через прямую…

а) параллельную данной плоскости

б) перпендикулярную данной плоскости

в) не перпендикулярную данной плоскости

Вариант 1

7. Количество двугранных углов параллелепипеда равно ….

б) 12

а) 8

в) 24

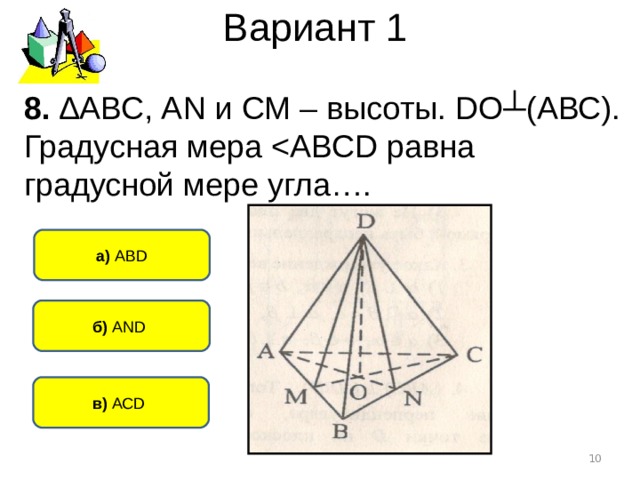
Вариант 1

8. ∆АВС, А N и СМ – высоты. D О┴(АВС). Градусная мера

а) АВ D

б) AND

в) АС D

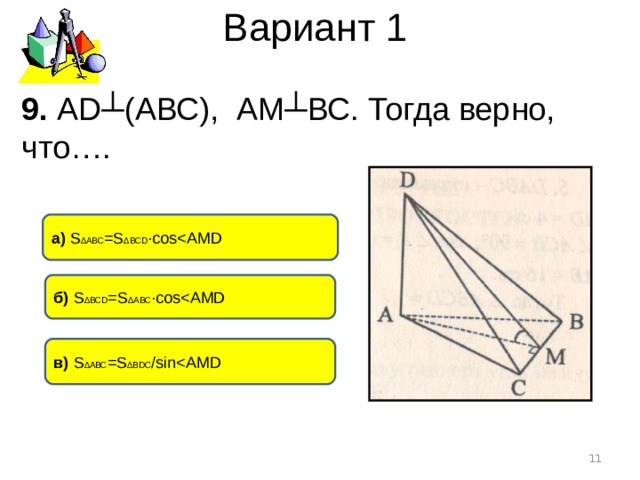
Вариант 1

9. А D ┴(АВС), АМ┴ВС. Тогда верно, что….

а) S ∆АВС = S ∆ ВС D ∙ cos

б) S ∆ВС D = S ∆ АВС ∙ cos

в) S ∆АВС = S ∆ В DC /sin

Вариант 1

10. Точка А находится на расстоянии 3см и 4см от двух перпендикулярных плоскостей. Тогда расстояние от точки А до прямой пересечения этих плоскостей равно….

б) 3

в) 4

а) 5

Вариант 1

1 1 . Равнобедренные треугольники АВС и ВС D с общим основанием не лежат в одной плоскости. Их высоты, проведенные к основанию, равны 2см, а расстояние между точками А и D равно 2√2см. Тогда градусная мера двугранного угла АВ CD равна

б) 90°

а) 30°

в) 60°

Вариант 1

12. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости α , катет наклонен к этой плоскости под углом 30°. Тогда угол наклона плоскости треугольника к плоскости α равен….

б) 45°

а) 90°

в) 30°

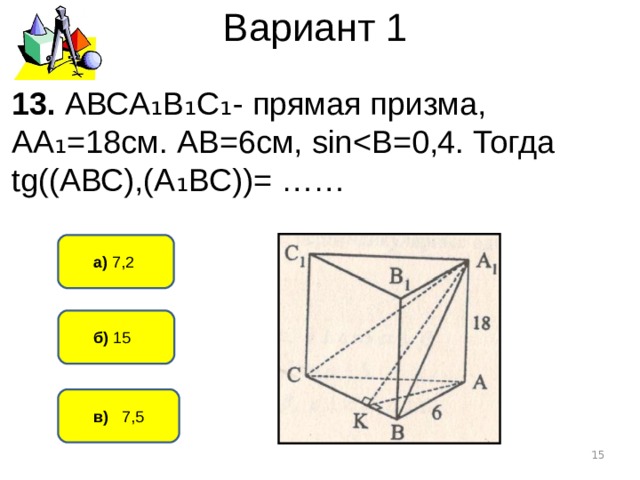
Вариант 1

13. АВСА ₁В₁С₁- прямая призма, АА₁=18см. АВ=6см, sin

а) 7,2

б) 15

в) 7,5

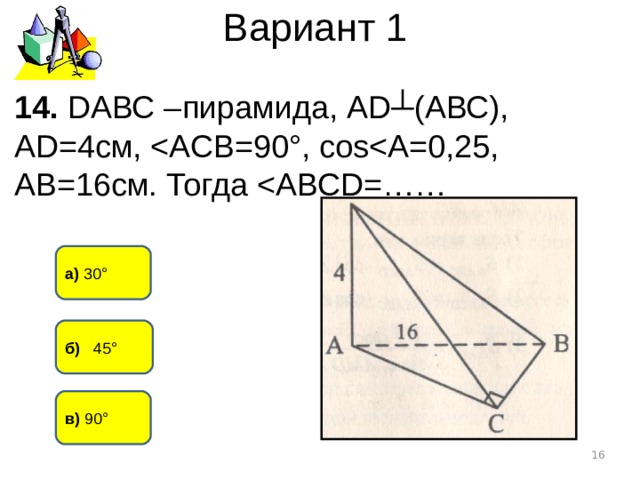
Вариант 1

14. D АВС – пирамида, А D ┴(АВС), А D =4см,

а) 30°

б) 45°

в) 90°

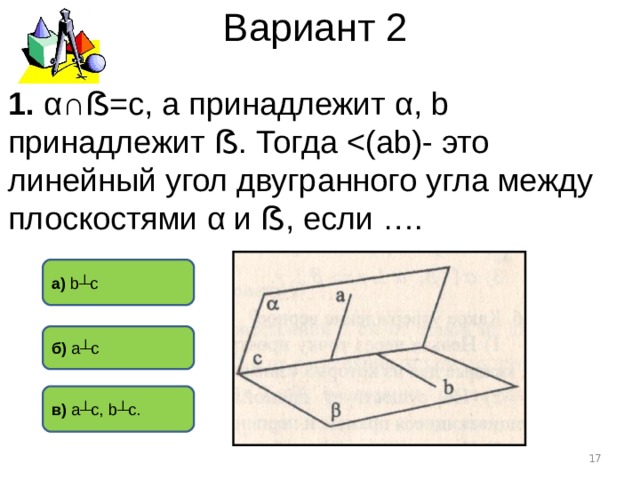
Вариант 2

1. α∩ ẞ =с, а принадлежит α , b принадлежит ẞ . Тогда

а) b┴c

б) a┴c

в) a┴c , b┴ с.

Вариант 2

2. Какое утверждение верное ?

а) Не может ребро двугранного угла быть не перпендикулярным любой прямой, лежащей в плоскости его линейного угла.

б) Не могут быть две плоскости, перпендикулярные третьей не параллельными.

в) Не могут быть две плоскости, перпендикулярные одной плоскости , не параллельными.

Вариант 2

3. Какое утверждение верное ?

а) если α∩ ẞ =с, а принадлежит α , b принадлежит ẞ , а ┴ с, b┴c , то α┴ ẞ

б) если α∩ ẞ =с, α┴ ẞ , а принадлежит α , b принадлежит ẞ , то а ┴b

в) если α∩ ẞ =с, α┴ ẞ , а принадлежит α , b принадлежит ẞ и а ┴c то а ┴b

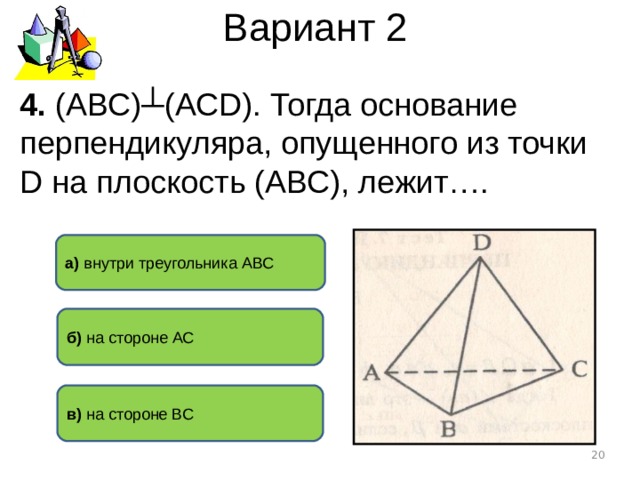
Вариант 2

4. (АВС)┴(АС D ). Тогда основание перпендикуляра, опущенного из точки D на плоскость (АВС ) , лежит….

а) внутри треугольника АВС

б) на стороне АС

в) на стороне ВС

Вариант 2

5. Какое утверждение верное ?

а) если α┴ ẞ , а принадлежит плоскости α , то а ┴ẞ

б) если α∩ ẞ =с, ɣ┴ с, то ɣ┴ α и ɣ┴ẞ

в) если α∩ ẞ , α┴ ɣ , то ẞ┴ɣ

Вариант 2

6. Какое утверждение верное ?

а) Нельзя через точку пространства провести три плоскости, каждые две из которых взаимно перпендикулярны.

б) Не существует прямой пересекающей две данные скрещивающиеся прямые и перпендикулярной каждой их них.

в) Не может плоскость быть не перпендикулярной данной плоскости, если она проходит через прямую, перпендикулярную данной плоскости .

Вариант 2

7. Количество двугранных углов тетраэдра равно ….

б) 6

а) 4

в) 12

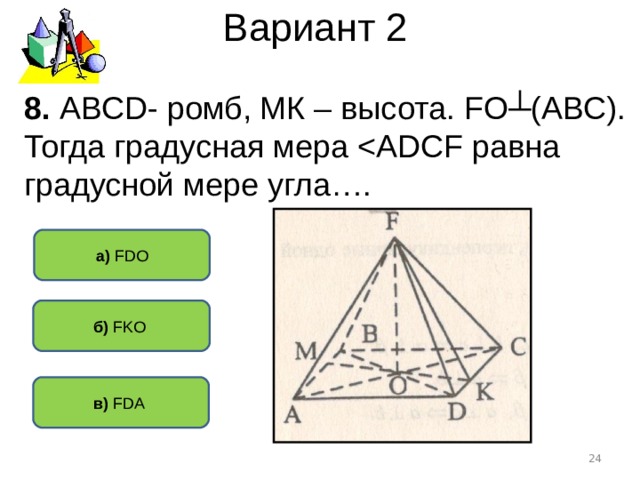
Вариант 2

8. АВС D - ромб, МК – высота. F О┴(АВС). Тогда градусная мера

а) FDO

б) FKO

в) FDA

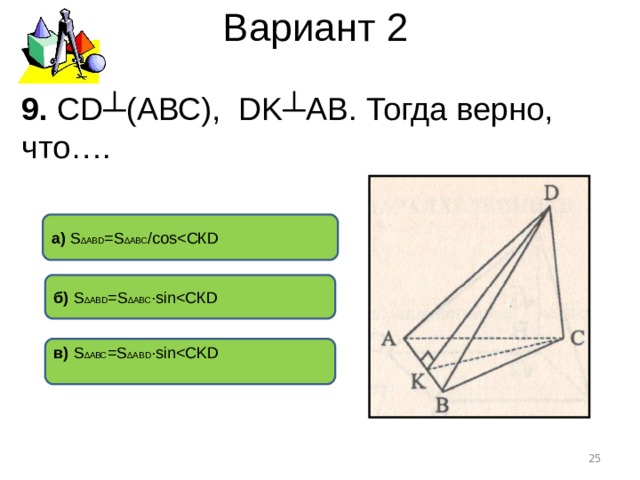
Вариант 2

9. CD ┴(АВС), DK ┴АВ. Тогда верно, что….

а) S ∆АВ D = S ∆ АВС /cos

б) S ∆АВ D = S ∆ АВС ∙ sin

в) S ∆АВС = S ∆ АВ D ∙ sin

Вариант 2

10. Точка А находится на расстоянии 1см от одной из двух перпендикулярных плоскостей и на расстоянии √5 см до линии пересечения этих плоскостей Тогда расстояние от точки А до второй плоскости равно....

б) 1

в) 3

а) 2

Вариант 2

1 1 . Равнобедренные треугольники АВС и ВС D не лежат в одной плоскости. Их высоты, проведенные к основанию ВС, равны 2см, и расстояние между точками А и D тоже равно 2см. Тогда градусная мера двугранного угла АВ CD равна

б) 60°

а) 30°

в) 45°

Вариант 2

12. Гипотенуза равнобедренного прямоугольного треугольника лежит в плоскости α , угол между плоскостью треугольника и плоскостью α равен 45°. Тогда угол градусная мера угла между катетом и плоскостью α равна….

б) 30°

а) 60°

в) 45°

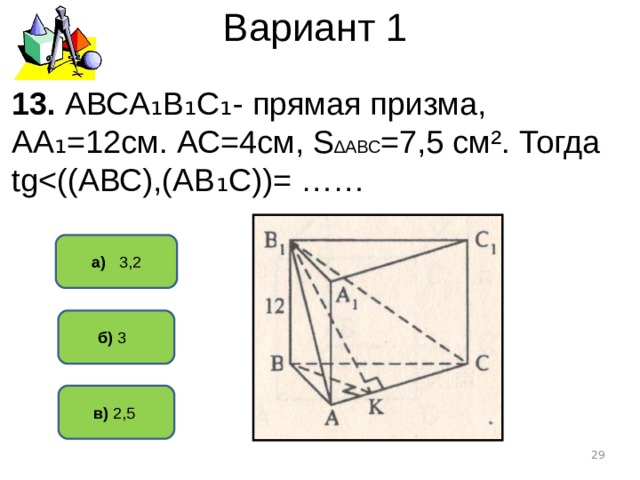
Вариант 1

13. АВСА ₁В₁С₁- прямая призма, АА₁=12см. АС=4см, S ∆АВС =7,5 см². Тогда tg

а) 3,2

б) 3

в) 2,5

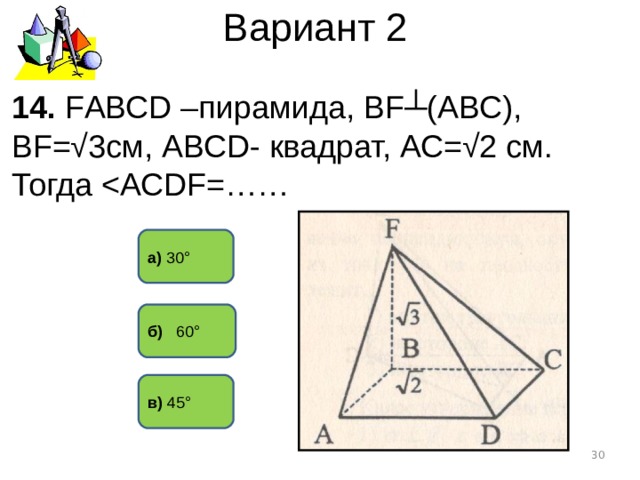
Вариант 2

14. F АВС D – пирамида, В F ┴(АВС), В F =√3см, АВС D - квадрат, АС=√2 см. Тогда

а) 30°

б) 60°

в) 45°

Ключи к тесту : Двугранный угол .

Перпендикулярность плоскостей.

1 вариант

Отв.

1

2

б

3

а

4

б

5

б

6

б

б

7

8

б

б

9

а

10

а

11

б

12

13

б

14

в

б

2 вариант

1

Отв.

в

2

3

а

4

в

5

б

б

6

7

в

б

8

9

б

10

а

11

а

б

12

13

б

а

14

б

Литература

Г.И. Ковалева, Н.И. Мазурова Геометрия 10-11 классы. Тесты для текущего и обобщающего контроля. Изд-во «Учитель», 2009г.