ГД 114 Математика
Преподаватель: Водяхина Н. В. Электронный адрес почты: nata.vodiahina2014@yandex.ru
Задание выдано 24.04.2020. Задание выполнить до следующего занятия!
Прочитать внимательно лекцию, законспектировать (если у кого нет!) и выполнить тест!
СФЕРА. ШАР
О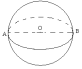 пределение. Шар- тело, которое состоит из всех точек пространства, находящих на расстоянии, не больше данного, от данной точки. Точка называется центром шара, а расстояние- радиусом шара.
пределение. Шар- тело, которое состоит из всех точек пространства, находящих на расстоянии, не больше данного, от данной точки. Точка называется центром шара, а расстояние- радиусом шара.
Граница шара называется шаровой поверхностью или сферой.
О – центр шара
ОА=ОВ – радиус шара
АВ – диаметр
В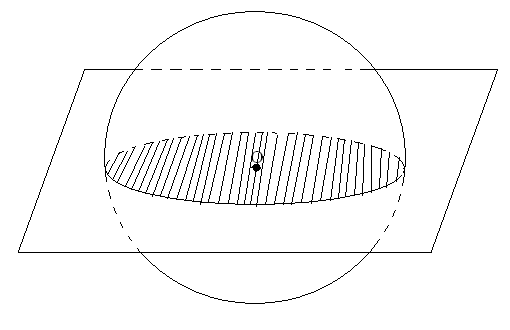 сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью.
сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью.
Теорема. Любая диаметральная плоскость шара является его плоскостью симметрии. Центр шара является его центром симметрии.
Определение. Плоскость, проходящая через точку А шаровой поверхности и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью. Точка А называется точкой касания.
Теорема. Касательная плоскость имеет с шаром только одну общую точку- точку касания.
П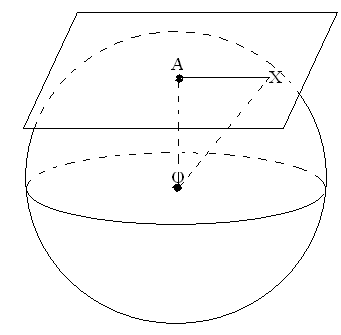 рямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания.
рямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания.
Теорема. Линия пересечения двух сфер есть окружность
Площадь сферы: 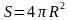
Объём шара: 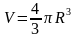
Тест по теме «Сфера и шар»
1. Выберите неверное утверждение.
а). сечение шара плоскостью есть окружность;
б). сфера может быть получена в результате вращения полуокружности
вокруг её диаметра;
в). тело, ограниченное сферой, называется шаром;
г). площадь сферы можно вычислить по формуле S = 4πr2.
2. Выберите верное утверждение.
а). отношение объёмов двух шаров равно 8, тогда отношение
площадей их поверхностей равно 4;
б). объём шара радиуса R равен 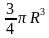 ;
;
в). шаровым сектором называется часть шара, отсекаемая от него
какой – нибудь плоскостью;
г). объём шарового слоя можно вычислить как сумму объёмов двух
шаровых сегментов.
3. Какое сечение шара плоскостью имеет наибольшую площадь?
а). сечение большого круга; б). сечение, перпендикулярное диаметру шара;
в). сечение, параллельное диаметру шара;
г). сечение, проходящее через точку, которая делит диаметр 3:2.
4. Какая фигура является пересечением двух больших кругов шара?
а). отрезок, который является диаметром данного шара; б). окружность;
в). круг; г). отрезок, который является радиусом данного шара.
5. Через всякие ли три точки можно провести сферу?
а). нет, точки, не должны принадлежать одной прямой; б). да;
в). да, если три точки лежат на одной прямой; г). нельзя ответить.
6. Сколько общих точек может иметь сфера и прямая?
а). две, одну, ни одной; б). две; в). одну; г). ни одной.
7. Сколько общих точек может иметь сфера и плоскость?
а). бесконечно много точек, принадлежащих окружности, одну, ни одной; б). одну;
в). ни одной; г). бесконечно много точек, принадлежащих окружности;
8. Шар, радиус которого 5 см, пересечен плоскостью на расстоянии 4 см
от центра. Найти площадь сечения.
а). 9π см2 ; б). π см2; в). 3π см2; г). 81π см2.
9. Через середину радиуса шара проведена плоскость перпендикулярная
к радиусу. Какая часть площади большого круга составляет площадь
круга, полученного в сечении?
а). ¾ большого круга; б). ½ большого круга;
в). 1/4 большого круга; г). 1/8 большого круга.
10. Сколько касательных плоскостей можно провести к данной сфере
через точку, проходящую вне сферы?
а). бесконечно много; б). одну; в). две; г). ни одной.
11. Найдите расстояние от центра шара до плоскости сечения, если объём шара равен 288π, а площадь сечения равна 27π.
а). 3; б). 2√3; в). 6; г). 3√2.
12. Объем параллелепипеда, описанного около сферы равен 216. Найти
радиус сферы.
а). 3; б). 6; в). 9; г). 8.





 пределение. Шар- тело, которое состоит из всех точек пространства, находящих на расстоянии, не больше данного, от данной точки. Точка называется центром шара, а расстояние- радиусом шара.
пределение. Шар- тело, которое состоит из всех точек пространства, находящих на расстоянии, не больше данного, от данной точки. Точка называется центром шара, а расстояние- радиусом шара. сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью.
сякое сечение шара плоскостью есть круг. Плоскость, проходящая через центр шара называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы- большой окружностью. рямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания.
рямая в касательной плоскости шара, проходящая через точку касания, называется касательной к шару в этой точке. Так как касательная плоскость имеет с шаром только одну общую точку, то касательная прямая тоже имеет с шаром только одну общую точку- точку касания. 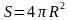
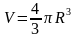
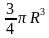 ;
;



















