Предмет: математика
Дата: 1.11.2021
Группа: 1-9 ^сварщик^
Преподаватель: Касымова У.Ш.
Тема : тест по тригонометрии
Вопрос № 1
tg(x)=
 sin(x)/cos(x)
sin(x)/cos(x)
 cos(x)/sin(x)
cos(x)/sin(x)
 все вышеперечисленное
все вышеперечисленное
Вопрос № 2
Что такое синус угла в прямоугольном треугольнике?
 отношение прилежащего катета к противолежащему
отношение прилежащего катета к противолежащему
 отношение противолежащего катета к гипотинузе
отношение противолежащего катета к гипотинузе
 отношение прилежащего катета к гипотинузе
отношение прилежащего катета к гипотинузе
Вопрос № 3
ctg(x)=
 sin(x)+cos(x)
sin(x)+cos(x)
 sin(x)/cos(x)
sin(x)/cos(x)
 cos(x)/sin(x)
cos(x)/sin(x)
 нет правильных ответов
нет правильных ответов
 ответ в) и г)
ответ в) и г)
Вопрос № 4
cos(0)=
 100
100
 0
0
 1
1
Вопрос № 5
sin(0)=
 0
0
 100
100
 1
1
Вопрос № 6
sin(2x)=
 2*tg(x)*cos(x)
2*tg(x)*cos(x)
 2*sin(x)*cos(x)
2*sin(x)*cos(x)
 2*tg(x)*ctg(x)
2*tg(x)*ctg(x)
Вопрос № 7
tg(x)*ctg(x)=
 0
0
 1
1
 бесконечность
бесконечность
Вопрос № 8
2*cos(x+y)=
 2*(cos(x)*cos(y)+sin(x)*sin(y))
2*(cos(x)*cos(y)+sin(x)*sin(y))
 2*(cos(x)*cos(y)-sin(x)*sin(y))
2*(cos(x)*cos(y)-sin(x)*sin(y))
 2*(cos(x)*sin(y)-sin(x)*cos(y))
2*(cos(x)*sin(y)-sin(x)*cos(y))
Вопрос № 9
sin(x+y)=
 cos(x)*sin(y)-sin(x)*cos(y)
cos(x)*sin(y)-sin(x)*cos(y)
 cos(x)*sin(y)+sin(x)*cos(y)
cos(x)*sin(y)+sin(x)*cos(y)
 cos(x)*cos(y)+sin(x)*sin(y)
cos(x)*cos(y)+sin(x)*sin(y)
Вопрос № 10
cos(-x)=
 -cos(x)
-cos(x)
 cos(x)
cos(x)
 0
0
Вопрос № 11
В какой четверти лежит угол в 340ͦ ?
а) 2 б) 3 в) 1 г) 4
Вопрос № 12
В какой четверти лежит угол в 1,8 рад.?
а) 4 б) 3 в) 2 г) 1
Вопрос № 13
В какой четверти лежит угол в 2,6 π ?
а) 1 б) 3 в) 4 г) 2
Вопрос № 14
Какой знак имеет выражение sin175ͦ cos280ͦ ?
а) + б) - в) нельзя определить
Вопрос № 15
Какой знак имеет выражение tg 410 сtg 5π/6 sin 0,3π ?
а) - б) нельзя определить в) +
Итог урока
оценивание
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Предмет: математика
Дата: 2.11.2021
Группа: 1-9 ^сварщик^
Преподаватель: Касымова У.Ш.
Тема: определения приращения функции в точке
Пусть x0 — стационарная точка, а х — произвольная точка, лежащая в некоторой окрестности стационарной точки x0. Разностью х — x0 называется приращение независимой переменной в точке x0 и обозначается Δх. Таким образом,
Δх = х - x0,
Значение функции f изменится на величину
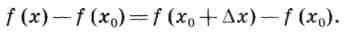
Эта разность называется приращением функции f в точке х0.
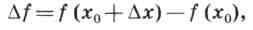
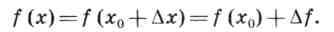
Обратите внимание: при фиксированном х0 приращение ∆f есть функция от ∆х.
Пример №1 Найдем приращение ∆х и ∆f в точке х0, если f(x) = x2, x0=2 и:
а) х=1,9
а) ∆x = x-x0 = 1,9 – 2 = -0,1
∆f=f(1,9) – f(2) = 1,92-22 = -0,39
перенесем x0 влево и получим, что х = x0 + Δх.
Δf =f(x0+Δx) - f(x0), откуда f(х) = f(x0+Δx) = f(x0) + Δf
Пример №2 Найдём приращения Δx и Δf в точке х0, если f(х) = x3, x0=3, х=1.6
Решение Δx = х - x0 = 1.6 - 3 = -1.4 ; Δf= f(1,6) - f(3) = 1,63 - 33= -22.904
Пример №3 Найдем приращения Δx и Δf в точке , если f(х)=x ,x0 = 1, х = 4
Пример №4 Найти приращение аргумента x, если он переходит от значения 3 к значению 3,2.
Пример №5 Найти приращение функции y=2x2 при x0=3 и и Δx=0,1
Пример №6 Найти приращение функции y=x2+3x в точке x0=0.
Пример №7 Найти приращение аргумента ∆х и приращение функции ∆f в точке х0, если f(х) = х2, x0=2 a) x=0.7 b) x =4.1
Итог урока
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Предмет: математика
Дата: 3.11.2021
Группа: 1-9 ^сварщик^
Преподаватель: Касымова У.Ш.
Тема: производные суммы, разности, произведения и частного
Правила вычисления производных.
Правило 1. Если функции и и v дифференцируемы в точке х0, то их сумма дифференцируема в этой точке и
(u + v)' = u' + v’
Коротко говорят: производная суммы равна сумме производных.
Правило 2. Если функции и и v дифференцируемы в точке х0, то их произведение дифференцируемо в этой точке и
(uv)' = u’v + uv’
Следствие. Если функция и дифференцируема в х0, а С — постоянная, то функция Сu дифференцируема в этой точке и
(Си)' = Си’
Коротко говорят: постоянный множитель можно выносить за знак производной.
Правило 3. Если функции и и v дифференцируемы в точке х0 и функция v не равна нулю в этой точке, то частное также дифференцируемо в х0
Задание №1Найти производную функции:
1)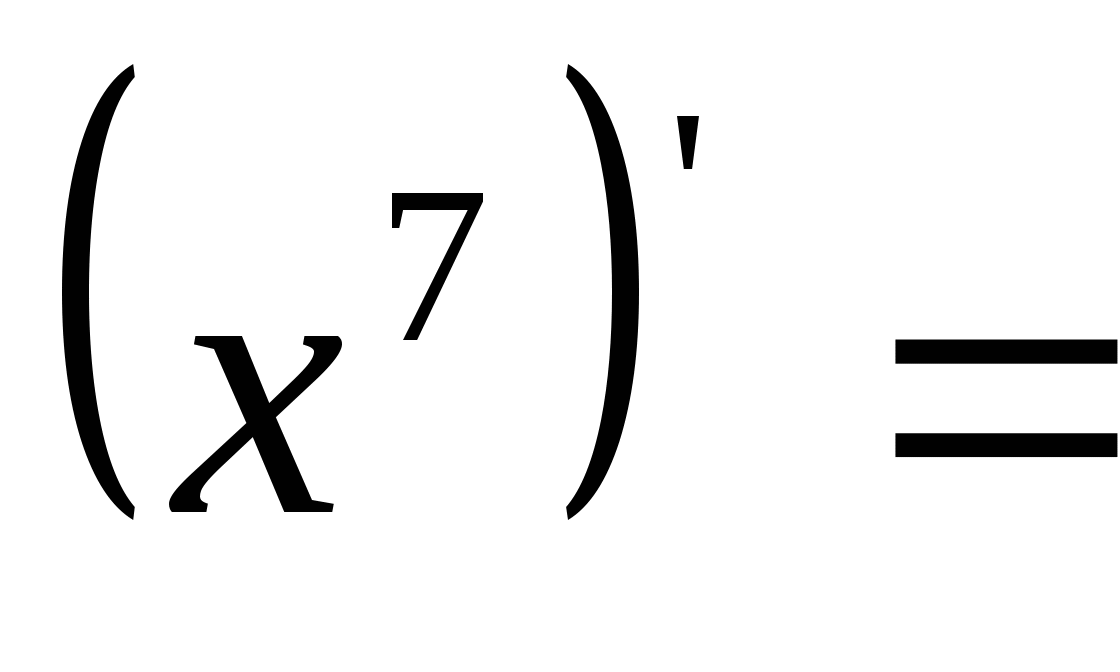 2)
2) 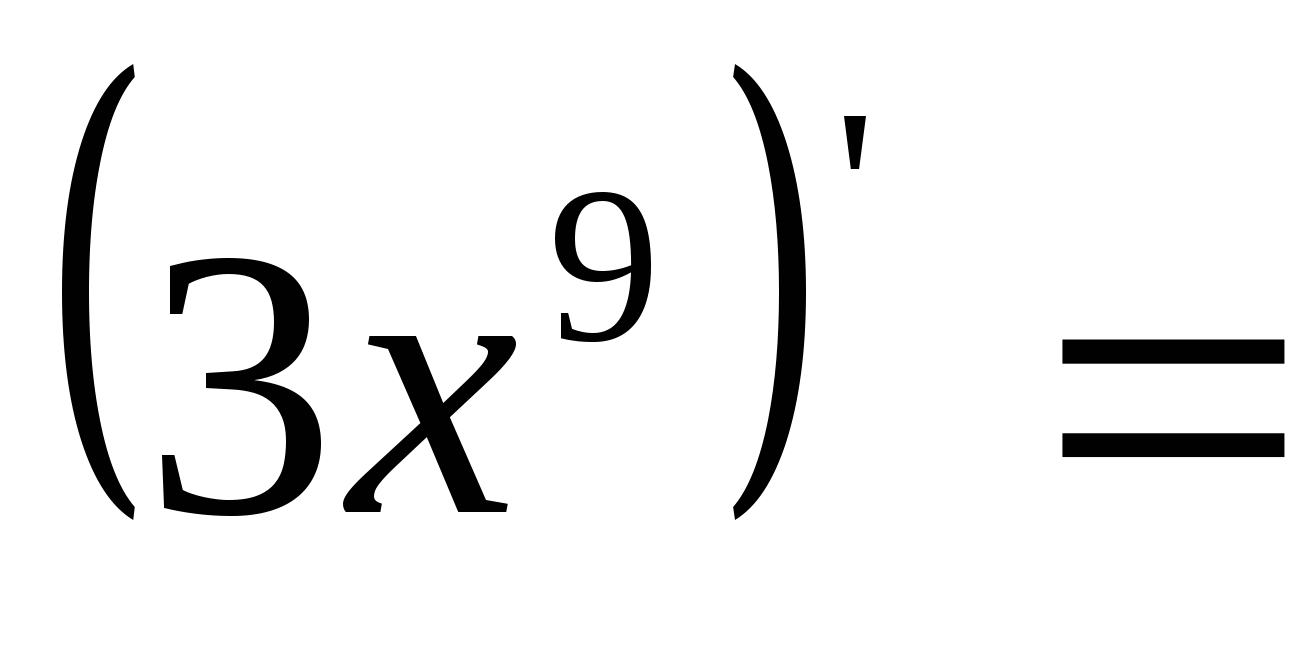 3)
3) 
4)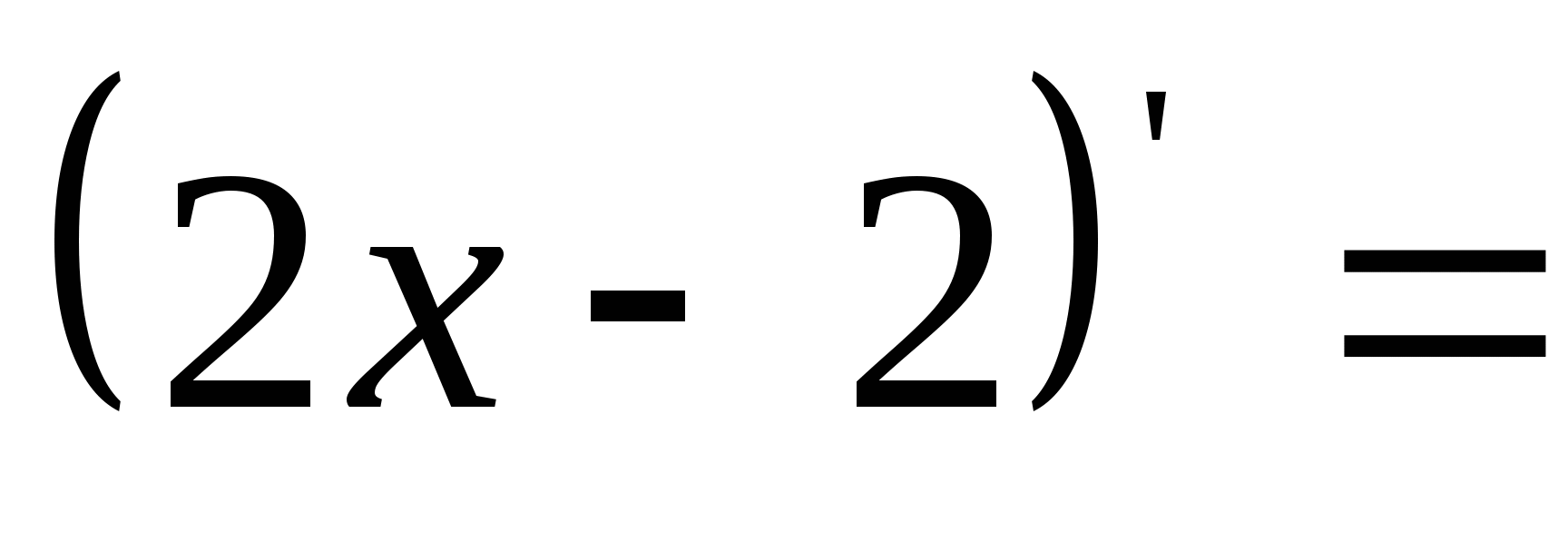 5) .
5) .  .6)
.6) 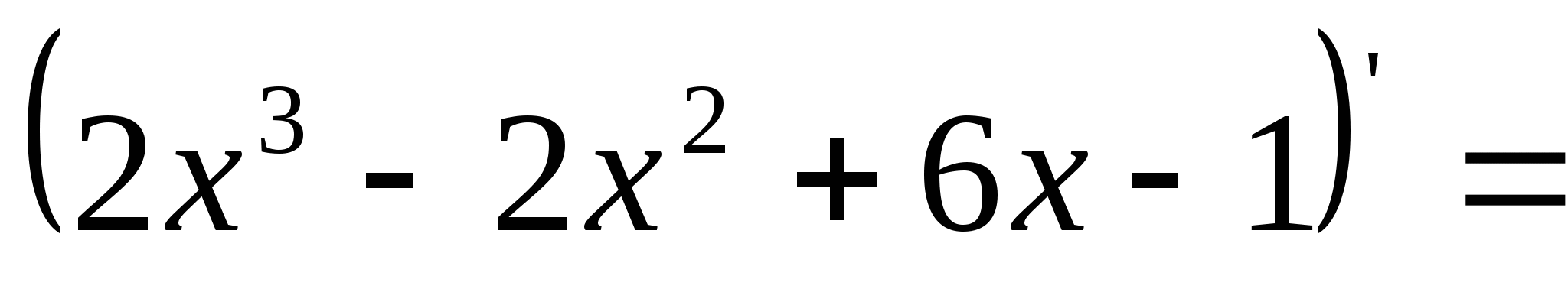
7) .8)
.8)  9) .
9) . 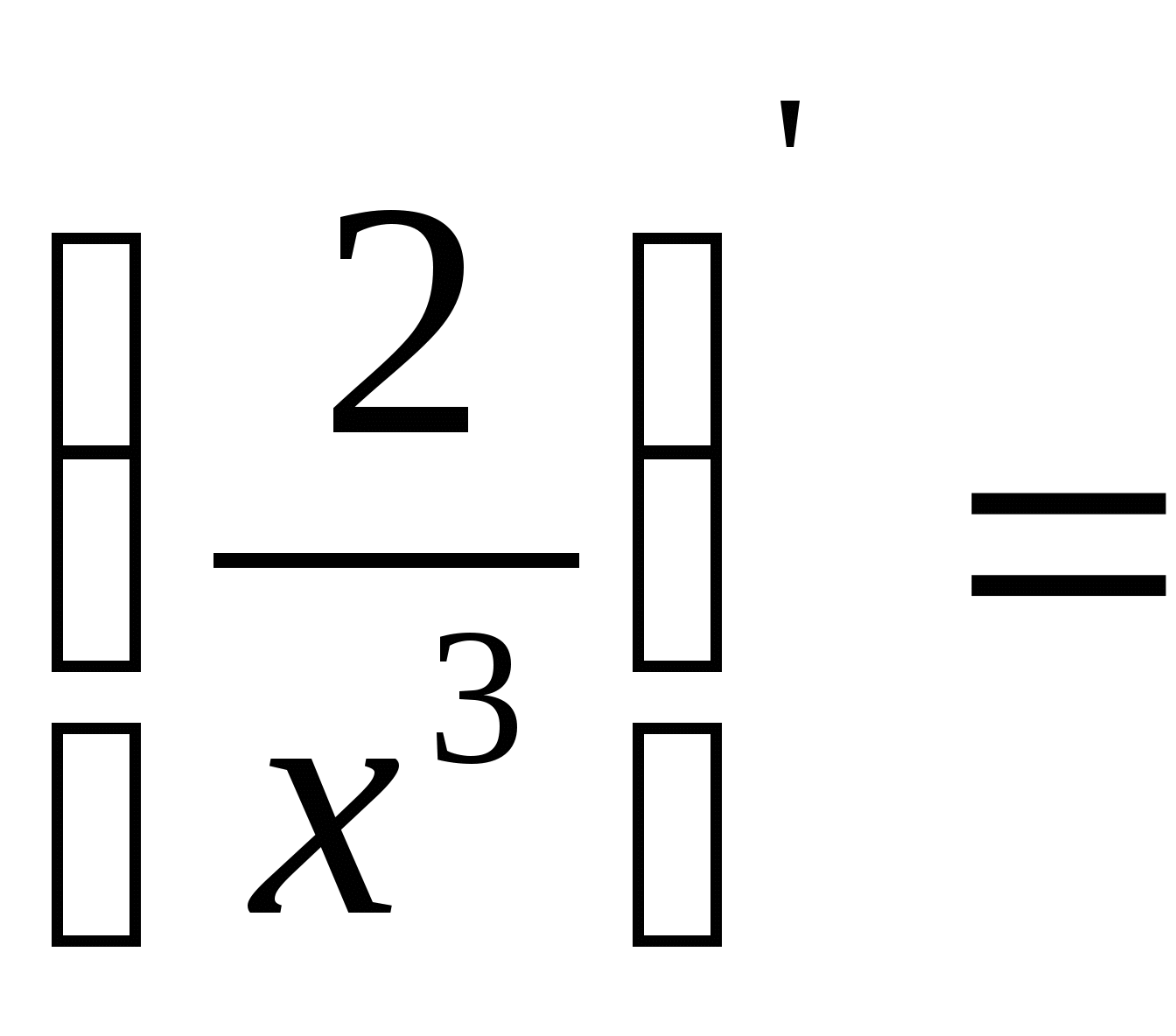
10) 11) .
11) . 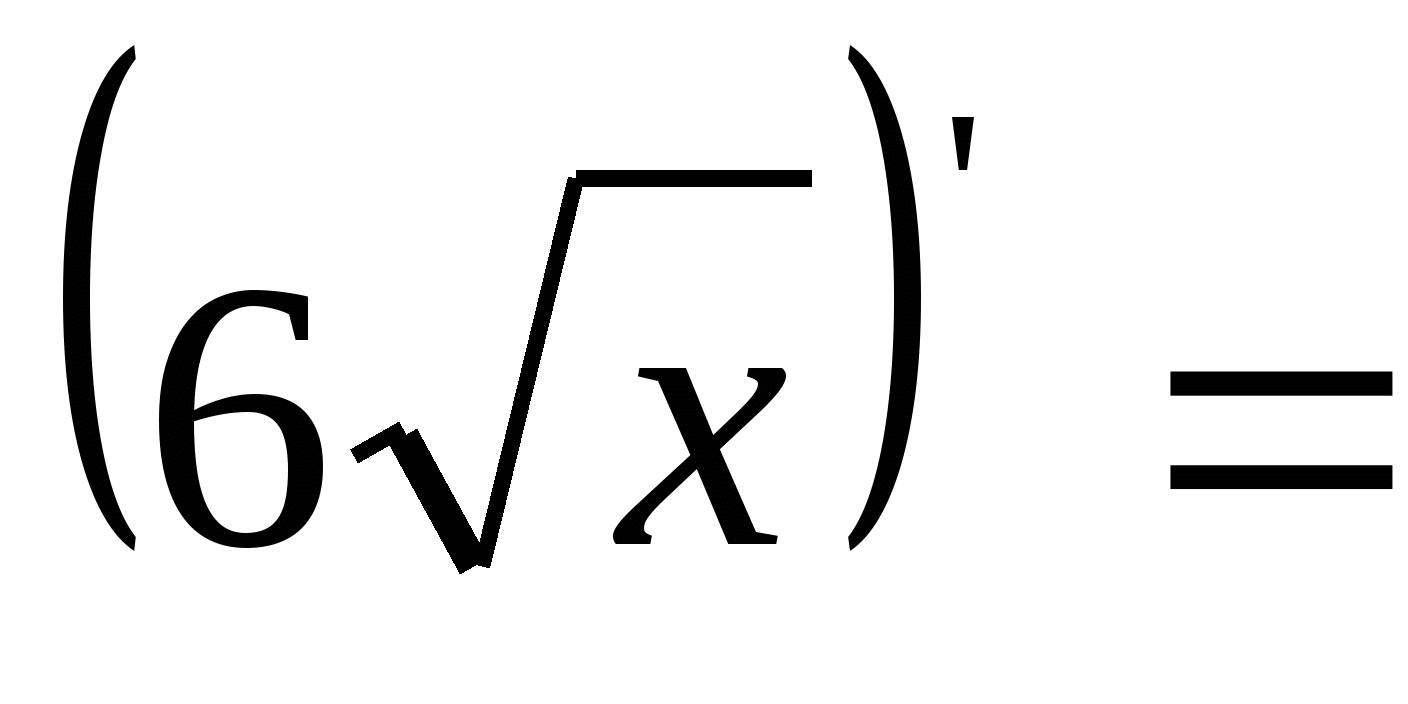 12).
12). 
13) 14).
14). 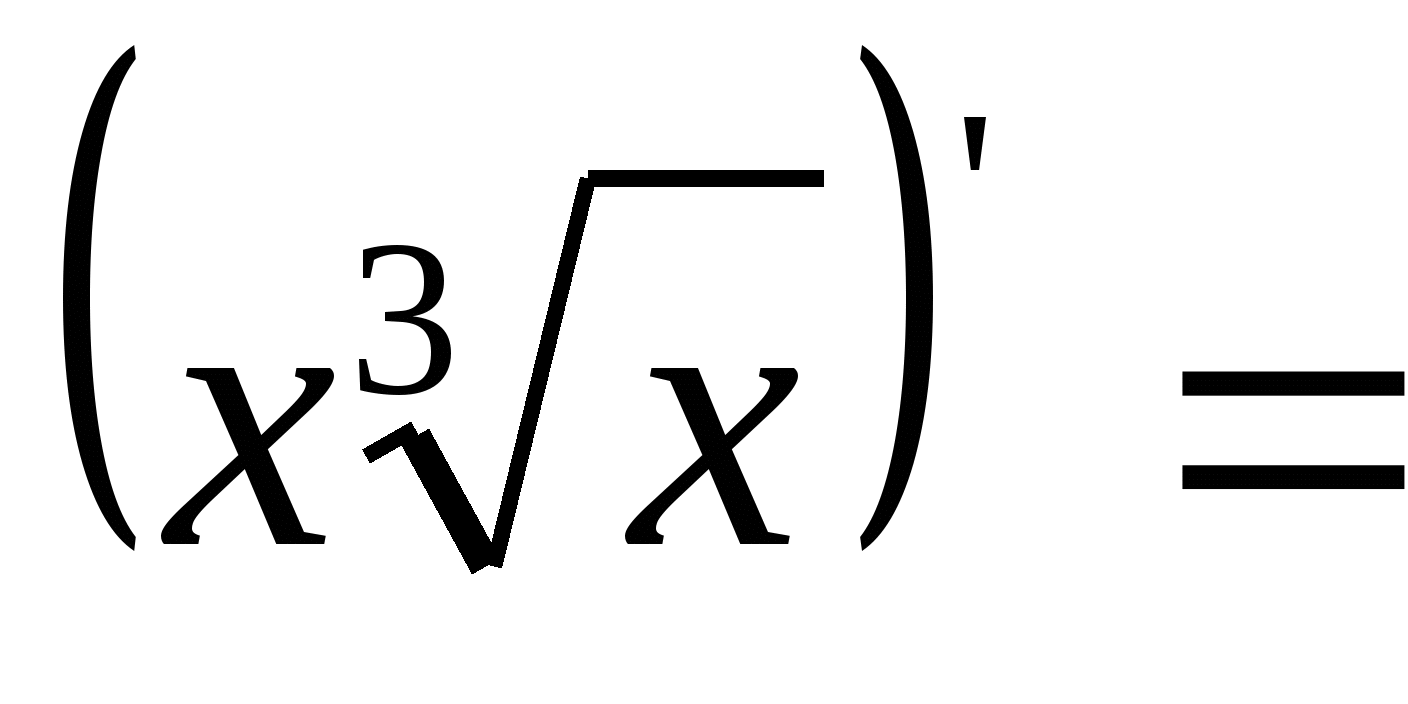 .15)
.15) 
16) 17) .
17) . 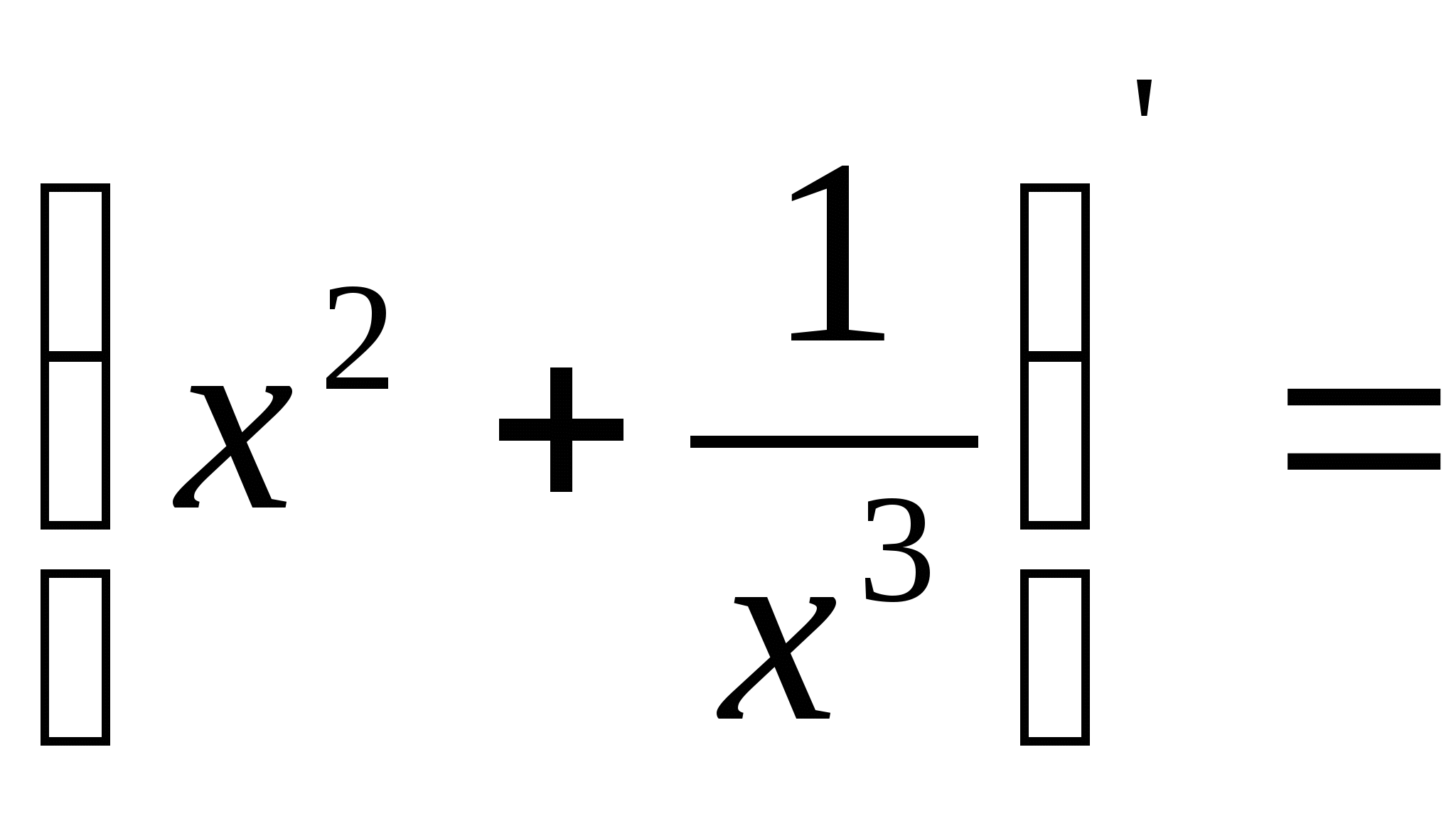 18) .
18) . 
19)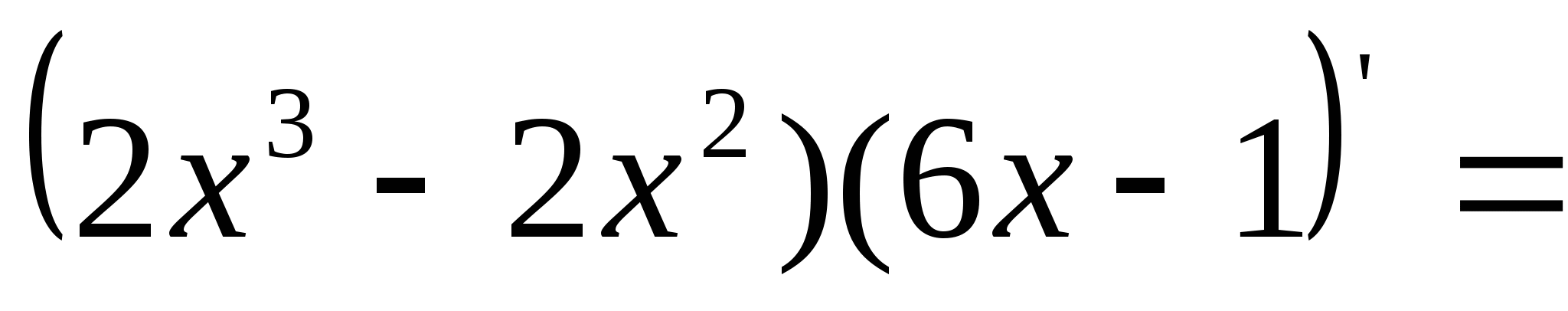 20).
20). 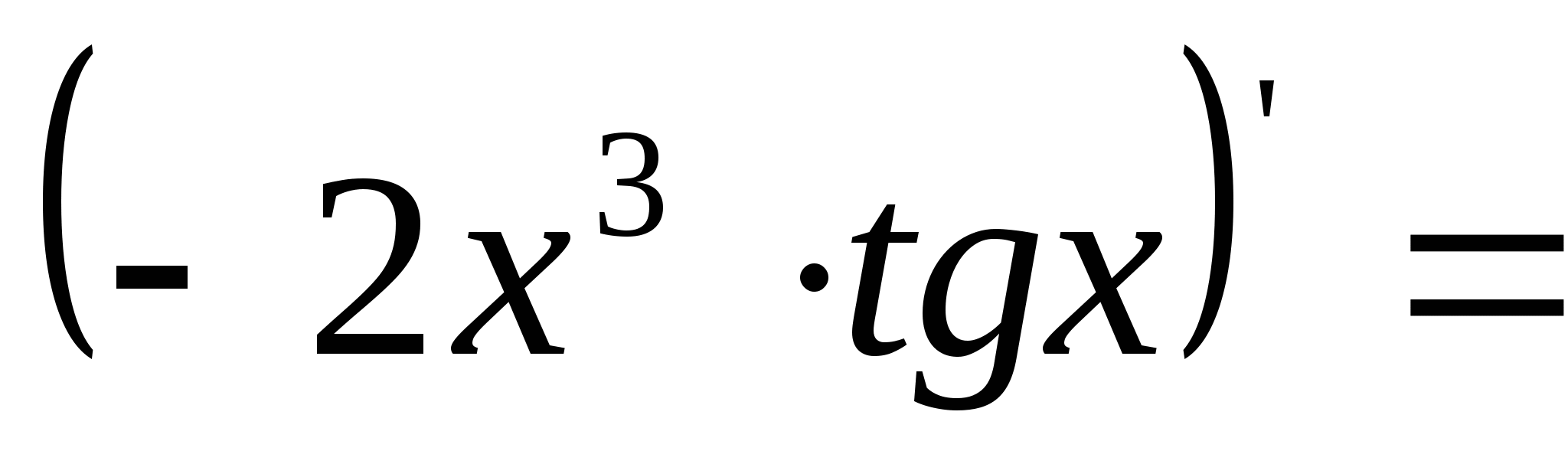 21).
21). 
Итог урока . оценивание
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Предмет: математика
Дата: 5.11.2021
Группа: 1-9 ^сварщик^
Преподаватель: Касымова У.Ш.
Тема: производная сложной функции

Задание№1
1) 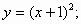
2) 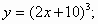
3) 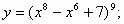
4)  ;
;
5) 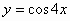 ;
;
6) 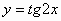 .
.
1) 
2) 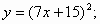
3) 
4)  ;
;
5) 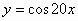 ;
;
6)  ;
;
7) 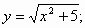
8) 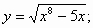
Задание №2 Найти производные функций. (А., В., С. – ответы)
| № | Задание | Ответы |
| А | В | С |
| 1 | 
| 
| 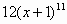
| 
|
| 2 | 
| 
| 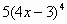
| 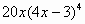
|
| 3 | 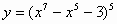
| 
| 
| 
|
| 4 | 
| 
| 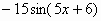
| 
|
| 5 | 
| 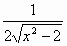
| 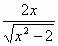
| 
|
Задание№3 Найти производные функций. (А., В., С. – ответы)
| № | Задание | Ответы |
| А | В | С |
| 1 | 
| 
| 
| 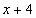
|
| 2 | 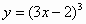
| 
| 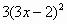
| 
|
| 3 | 
| 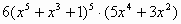
| 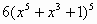
| 
|
| 4 | 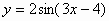
| 
| 
| 
|
| 5 | 
| 
| 
| 
|
Итог урока. Оценивание
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу






 sin(x)/cos(x)
sin(x)/cos(x) отношение прилежащего катета к противолежащему
отношение прилежащего катета к противолежащему
 17) .
17) . 












