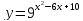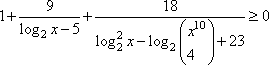Тест в формате ЕГЭ 10 класс Вариант 16

Задание 1. Призерами городской олимпиады по математике стало 48 учеников, что составило 12% от числа участников. Сколько человек участвовало в олимпиаде?

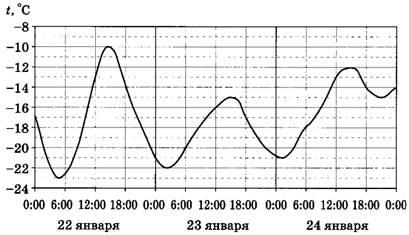
Задание 2. На рисунке показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 24 января. Ответ дайте в градусах Цельсия.

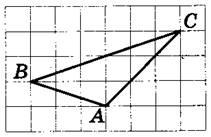
Задание 3. На клетчатой бумаге с размером клетки 1x1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

Задание 4. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства».

Задание 5. Найдите корень уравнения .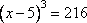

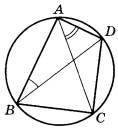
Задание 6. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 36°, угол CAD равен 52°. Найдите угол ABC. Ответ дайте в градусах.

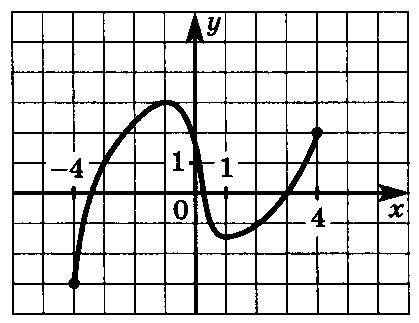
Задание 7. Найти длину промежутков возрастания функции

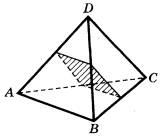
Задание 8. Рёбра правильного тетраэдра ABCD равны 42. Найдите площадь сечения, проходящего через середины рёбер AC, AD и BD.

Задание 9. Найдите значение выражения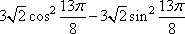 

Задание 10. В ходе распада радиоактивного изотопа его масса уменьшается по закону 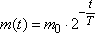, где m0 (мг) — начальная масса изотопа, t (мин) — время, прошедшее от начального момента, Т (мин) — период полураспада. В начальный момент времени масса изотопа m0 = 80 мг. Период его полураспада Т = 2 мин. Через сколько минут масса изотопа будет равна 5 мг?

Задание 11. Моторная лодка прошла против течения реки 112 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 11 км/ч. Ответ дайте в км/ч.

Задание 12. Найдите наименьшее значение функции

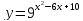
Задание 13. а) Решите уравнение .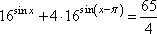

б) Укажите корни этого уравнения, принадлежащие отрезку .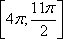

Задание 14. В кубе ABCDA1B1C1D1 все рёбра равны 4. На его ребре ВВ1 отмечена точка K так, что KB=3. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.

а) Докажите, что A1P:PB1 =2:1, где Р — точка пересечения плоскости α с ребром А1В1.

б) Найдите угол наклона плоскости α к плоскости грани ВВ1С1C.

Задание 15. Решите неравенство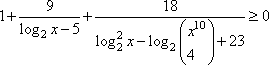 

Задание 16. Четырёхугольник ABCD вписан в окружность, причём сторона CD — диаметр этой окружности. Продолжение перпендикуляра АН к диагонали BD пересекает сторону CD в точке а окружность — в точке F, причём Н — середина АЕ.

а) Докажите, что четырёхугольник BCFE — параллелограмм.

б) Найдите площадь четырёхугольника ABCD, если известно, что АВ = 5 и АН = 4.

Задание 17. В июле 2020 года планируется взять кредит в банке на сумму 928 200 рублей. Условия его возврата таковы:

— каждый январь долг увеличивается на 10 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.

Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года)?

Задание 18. Найти все значения параметра a, при каждом из которых для любой пары (u; v) действительных чисел u и v выполнено неравенство

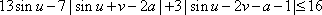
Задание 19. Маша и Наташа делали фотографии несколько дней подряд. В первый день Маша сделала m фотографий, а Наташа — n фотографий. В каждый следующий день каждая из девочек делала на одну фотографию больше, чем в предыдущий день. Известно, что Наташа за всё время сделала суммарно на 1173 фотографии больше, чем Маша, и что фотографировали они больше одного дня.

а) Могли ли они фотографировать в течение 17 дней?

б) Могли ли они фотографировать в течение 18 дней?

в)  Какое наибольшее суммарное число фотографий могла сделать Наташа за все дни фотографирования, если известно, что в последний день Маша сделала меньше 45 фотографий?