ЕГЭ. МАТЕМАТИКА. Профильный уровень. 2018 г. 107
Единый государственный экзамен по МАТЕМАТИКЕ
Вариант 107
Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой, капиллярной или перьевой ручек.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
Справочные материалы





Часть 1
| Ответом к заданиям 1–12 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно. |
Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продаёт с наценкой 20%. Какое наибольшее количество таких горшков можно купить в этом магазине на 1100 рублей?
Ответ: ________________
П ри работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси —напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение за первые 11 часов работы фонарика.
ри работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси —напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение за первые 11 часов работы фонарика.
Ответ: ________________
П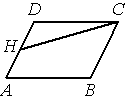 лощадь параллелограмма ABCD равна 30. Точка H— середина стороны АD. Найдите площадь трапеции AHCB.
лощадь параллелограмма ABCD равна 30. Точка H— середина стороны АD. Найдите площадь трапеции AHCB.
Ответ: ________________
В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Ответ: ________________
Найдите корень уравнения 
 Ответ: ________________
Ответ: ________________
В треугольнике ABC угол B равен 45°, угол C равен 85°, AD— биссектриса, E— такая точка на AB, что AE=AC. Найдите угол BDE. Ответ дайте в градусах.
Ответ: ________________

На рисунке изображён график функции y=f(x), определённой на интервале (− 7; 7). Определите количество целых точек, в которых производная функции положительна.
Ответ: ________________
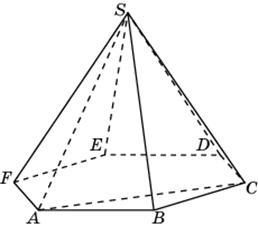
Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
Ответ: ________________
Часть 2
Найдите значение выражения: 
Ответ: ________________
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна  , где
, где  — ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания
— ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания  ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)
Ответ: ________________
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Ответ: ________________
Найдите наименьшее значение функции

на отрезке 
Ответ: _______________
| Не забудьте перенести все ответы в БЛАНК ОТВЕТОВ № 1. |
| Для записи решений и ответов на задания 13-19 используйте БЛАНК ОТВЕТОВ № 2. Запишите сначала номер выполняемого задания (13, 14 и т.д.), а затем полное обоснованное решение и ответ. Ответы записывайте четко и разборчиво. |
а) Решите уравнение

б) Найдите все корни этого уравнения, принадлежащие отрезку 
SABCD — правильная пирамида с вершиной S. Из точки В опущен перпендикуляр BH на плоскость SAD.
а) Доказать, что угол AHC=90 °.
б) Найдите объем пирамиды, если HA=1 и HC=7.
Решите неравенство

Дан прямоугольный треугольник ABC с прямым углом C. На катете AC взята точка M. Окружность с центром O и диаметром CM касается гипотенузы в точке N.
а) Докажите, что прямые MN и BO параллельны.
б) Найдите площадь четырёхугольника BOMN, если CN=4 и AM:MC=1:3.
Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме  Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме
Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме  Гбайт входящей в него информации выходит 21t Гбайт обработанной информации; 25
Гбайт входящей в него информации выходит 21t Гбайт обработанной информации; 25
Найдите значения a, при каждом из которых система уравнений

имеет единственное решение.
Задумано несколько целых чисел. Набор этих чисел и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Например, если задуманы числа 2, 3, 5, то на доске будет выписан набор 2, 3, 5, 5, 7, 8, 10.
а) На доске выписан набор − 8, − 5, − 4, − 3, − 1, 1, 4. Какие числа были задуманы?
б) Для некоторых различных задуманных чисел в наборе, выписанном на доске, число 0 встречается ровно 2 раза. Какое наименьшее количество чисел могло быть задумано?
в) Для некоторых задуманных чисел на доске выписан набор. Всегда ли по этому набору можно однозначно определить задуманные числа?
| Ответы |
|
|
| №1 | 7 |
| №2 | 0,6 |
| №3 | 22,5 |
| №4 | 0,9975 |
| №5 | 1,5 |
| №6 | 40 |
| №7 | 8 |
| №8 | 6 |
| №9 | -7 |
| №10 | 4 |
| №11 | 4 |
| №12 | - 6 |
| №13 | 
|
| №14 | б)  |
| №15 | |
| №16 | б) 7 |
| №17 | 1682 |
| №18 | 
|
| №19 | а) -5, -3, 4; б) 4; в) нет |
© 2018 г. egemath.ru.
Допускается копирование в образовательных некоммерческих целях.












 ри работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси —напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение за первые 11 часов работы фонарика.
ри работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси —напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение за первые 11 часов работы фонарика. лощадь параллелограмма ABCD равна 30. Точка H— середина стороны АD. Найдите площадь трапеции AHCB.
лощадь параллелограмма ABCD равна 30. Точка H— середина стороны АD. Найдите площадь трапеции AHCB. 
 Ответ: ________________
Ответ: ________________


 , где
, где  — ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания
— ЭДC источника (в вольтах), r=1 Ом — его внутреннее сопротивление, R — сопротивление цепи (в омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более 20% от силы тока короткого замыкания  ? (Ответ выразите в омах.)
? (Ответ выразите в омах.)




 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме
Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме 











