ПЕРЕМЕННАЯ Х СИСТЕМЫ УРАВНЕНИЙ
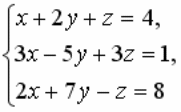
ОПРЕДЕЛЯЕТСЯ ПО ФОРМУЛЕ:
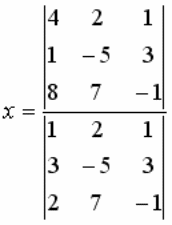
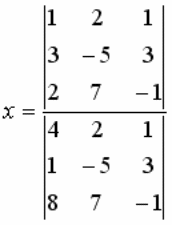
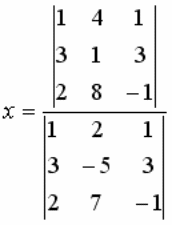
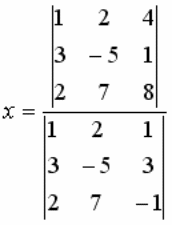
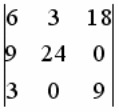
ОПРЕДЕЛИТЕЛЬ 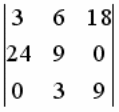 МОЖНО ПРИВЕСТИ К ВИДУ:
МОЖНО ПРИВЕСТИ К ВИДУ:

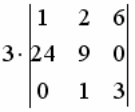
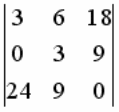
КВАДРАТНАЯ МАТРИЦА 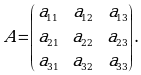 ИМЕЕТ ПОРЯДОК :
ИМЕЕТ ПОРЯДОК :
первый
второй
третий
четвертый
УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ДАННЫЕ ТОЧКИ 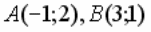 ИМЕЕТ ВИД:
ИМЕЕТ ВИД:
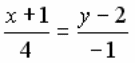
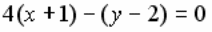
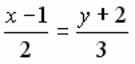
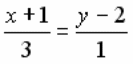
МАТРИЦА 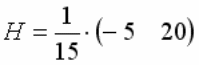 ИМЕЕТ РАЗМЕРНОСТЬ:
ИМЕЕТ РАЗМЕРНОСТЬ:
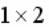
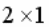
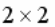
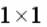
УРАВНЕНИЕ 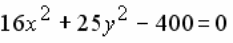 ЗАДАЕТ НА ПЛОСКОСТИ:
ЗАДАЕТ НА ПЛОСКОСТИ:
эллипс
окружность
гиперболу
параболу
ДЛИНА ВЕКТОРА 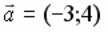 РАВНА:
РАВНА:
5
1
7
4
РАСПОЛОЖЕНИЕ УРАВНЕНИЯ ПРЯМОЙ НА КООРДИНАТНОЙ ПЛОСКОСТИ:
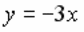
уравнение прямой, проходящей через начало координат
уравнение прямой параллельной оси ОУ
уравнение прямой параллельной оси ОZ
уравнение прямой параллельной оси ОX
ЗНАЧЕНИЕ ПРЕДЕЛА 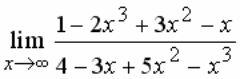 РАВНО:
РАВНО:
2
0
0,5
1/4
ФУНКЦИЯ f(х) ИМЕЕТ В ТОЧКЕ Х0 РАЗРЫВ 1 РОДА:
когда существуют конечные равные односторонние пределы функции слева и справа
когда существуют конечные не равные односторонние пределы функции слева и справа
когда хотя бы один из односторонних пределов слева или справа, равен бесконечности или не существует
когда существуют конечные равные односторонние пределы функции слева и справа
ЭКСЦЕНТРИСИТЕТ ЭЛЛИПСА 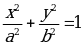 ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:
ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:
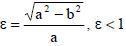
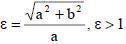
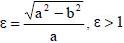
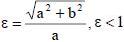
МНОЖЕСТВО ВСЕХ ТОЧЕК ПЛОСКОСТИ, СУММА РАССТОЯНИЙ ОТ КАЖДОЙ ИЗ КОТОРЫХ ДО ДВУХ ДАННЫХ ТОЧЕК ЭТОЙ ПЛОСКОСТИ, НАЗЫВАЕМЫХ ФОКУСАМИ, ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ, НАЗЫВАЕТСЯ
эллипсом
гиперболой
окружностью
овалом
ЕСЛИ ПЛОСКОСТЬ ЗАДАНА УРАВНЕНИЕМ Ax+By+D=0, ТО ОНА
параллельно оси Оz
параллельно оси Ох
параллельно оси уОz
проходит через начало координат
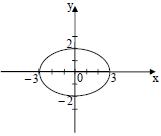 КРИВАЯ, ИЗОБРАЖЕННАЯ НА РИСУНКЕ, ОПРЕДЕЛЯЕТСЯ УРАВНЕНИЕМ:
КРИВАЯ, ИЗОБРАЖЕННАЯ НА РИСУНКЕ, ОПРЕДЕЛЯЕТСЯ УРАВНЕНИЕМ:
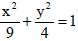
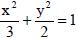
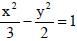
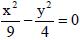
РАССТОЯНИЕ ОТ ТОЧКИ М0(х0;у0) ДО ПРЯМОЙ Ах+Ву+С=0 ВЫЧИСЛЯЕТСЯ ПО ФОРМУЛЕ:
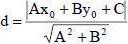
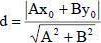
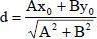
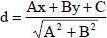
ПРЕДЕЛ ОТНОШЕНИЯ ПРИРАЩЕНИЯ ФУНКЦИИ y = f(x0+Dx) - f(x0) К ПРИРАЩЕНИЮ АРГУМЕНТА x ПРИ СТРЕМЛЕНИИ x К НУЛЮ НАЗЫВАЕТСЯ
производной функции f(x)
первым замечательным пределом
первообразной функцией f(x)
вторым замечательным пределом
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ ВЫЧИСЛЯЕТСЯ ТАК:
вычисляем производную внешней функции не изменяя внутреннюю функцию.
вычисляем производную внешней функции, не изменяя внутреннюю функцию, и умножаем на производную внутренней функции..
вычисляем производную внутренней функции, не изменяя внешнюю функцию, и умножаем на внутреннюю функции..
вычисляем производную внутренней функции, не изменяя внешнюю функцию.
ДЛЯ ВЫЧИСЛЕНИЯ ПРОИЗВОДНОЙ ПРОИЗВЕДЕНИЯ ИСПОЛЬЗУЮТ ФОРМУЛУ
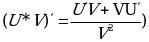
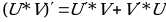
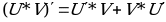
(U*V)'=U'*V-U*V'
НЕОБХОДИМЫМ УСЛОВИЕМ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ 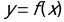 В ТОЧКЕ ЯВЛЯЕТСЯ, УСЛОВИЕ
В ТОЧКЕ ЯВЛЯЕТСЯ, УСЛОВИЕ
первая производная равна нулю
первая производная больше нуля
первая производная меньше нуля
первая производная равна 1
ПРАВИЛЬНЫМ ОТВЕТОМ, В ДАННОМ ПРИМЕРЕ 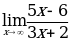 ЯВЛЯЕТСЯ
ЯВЛЯЕТСЯ
0,6
-1
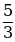
1
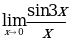 РАВЕН:
РАВЕН:
0
3
1/3
0,5
ВЫЧИСЛИТЬ ЗНАЧЕНИЕ ПРЕДЕЛА 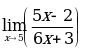
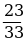
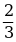
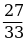
0,5
ЗНАЧЕНИЕ 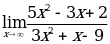 РАВНО:
РАВНО:
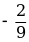
-3
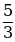
2
ПРИ РЕШЕНИИ НЕОПРЕДЕЛЕННОСТИ ВИДА 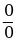 В ПРИМЕРЕ
В ПРИМЕРЕ 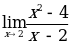 ПОЛУЧИТСЯ:
ПОЛУЧИТСЯ:
4
0
3
ПРИ РЕШЕНИИ НЕОПРЕДЕЛЕННОСТИ ВИДА 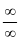 В ПРИМЕРЕ
В ПРИМЕРЕ 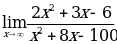 ПОЛУЧИТСЯ:
ПОЛУЧИТСЯ:
2
3/8
4
3
МАТРИЦЕЙ РАЗМЕРА m х n НАЗЫВАЕТСЯ:
совокупность m произвольных строк и n произвольных столбов чисел
прямоугольная таблица, содержащая m строк и n столбцов
любая совокупность 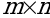 чисел
чисел
квадратная таблица, содержащая m строк и n столбцов
ДВЕ МАТРИЦЫ НАЗЫВАЮТСЯ РАВНЫМИ ЕСЛИ:
они имеют одинаковую размерность
они имеют равное количество строк и столбцов и совпадают поэлементно
они имеют одинаковую размерность и совпадают поэлементно
если все ее элементы равны нулю
МАТРИЦА НАЗЫВАЕТСЯ КВАДРАТНОЙ, ЕСЛИ:
сумма квадратов всех ее элементов неотрицательна
число ее строк равно числу ее столбцов
элементы матрицы имеют одинаковую размерность
сумма квадратов всех ее элементов неотрицательна
МАТРИЦА НАЗЫВАЕТСЯ НУЛЕВОЙ, ЕСЛИ
все ее элементы равны нулю
она содержит нули
ниже (выше) диагонали стоят только нули
одна строка (столбец) содержат нули
ЕДИНИЧНОЙ НАЗЫВАЕТСЯ КВАДРАТНАЯ МАТРИЦА, У КОТОРОЙ
все недиагональные элементы равны единице, а диагональные элементы равны нулю
все элементы равны единицы
все диагональные элементы равны единице, а недиагональные элементы равны нулю
столбец (строка) равны единице
МАТРИЦА 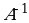 НАЗЫВАЕТСЯ ОБРАТНОЙ К МАТРИЦЕ А, ЕСЛИ
НАЗЫВАЕТСЯ ОБРАТНОЙ К МАТРИЦЕ А, ЕСЛИ
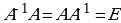
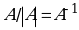
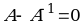
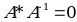
ВЕКТОРЫ ЯВЛЯЮТСЯ КОЛЛИНЕАРНЫМИ, ЕСЛИ
они лежат в параллельных плоскостях
они лежат на пересекающихся прямых
если они лежат на одной прямой или на параллельных прямых
они лежат на перпендикулярных прямых
НУЛЕВЫМ НАЗЫВАЮТ ВЕКТОР
вектор, лежащий на одной прямой
вектор, единичной длины
вектор , имеющий противоположное направление
если начало и конец вектора совпадают
ПРОТИВОПОЛОЖНЫМ ВЕКТОРОМ 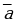 К ВЕКТОРУ
К ВЕКТОРУ 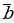 НАЗЫВАЮТ ВЕКТОР
НАЗЫВАЮТ ВЕКТОР
имеющий противоположные по знаку координаты
имеющий одинаковые координаты
имеющий нулевые координаты
коллинеарный к вектору а
УСЛОВИЕ ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМЫХ A1x + B1y + C1 = 0 и A2x + B2y + C2 = 01 = 0
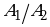 =
= 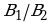
A1A2 - B1B2 = 0
A1A2 + B1B2 = 0
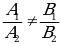







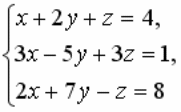

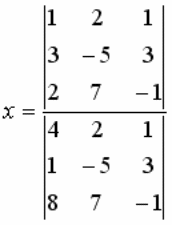


 МОЖНО ПРИВЕСТИ К ВИДУ:
МОЖНО ПРИВЕСТИ К ВИДУ:



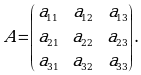 ИМЕЕТ ПОРЯДОК :
ИМЕЕТ ПОРЯДОК :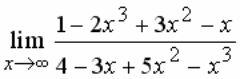 РАВНО:
РАВНО: КРИВАЯ, ИЗОБРАЖЕННАЯ НА РИСУНКЕ, ОПРЕДЕЛЯЕТСЯ УРАВНЕНИЕМ:
КРИВАЯ, ИЗОБРАЖЕННАЯ НА РИСУНКЕ, ОПРЕДЕЛЯЕТСЯ УРАВНЕНИЕМ:









