Тест по теме: «Окружность» 8 класс
1- вариант
1. Выбрать верные утверждения: а) угол с вершиной на окружности называется её центральным углом; б) центральный угол измеряется дугой , на которую он опирается; в) угол, образованный двумя хордами окружности, называется вписанным углом этой окружности; г) вписанный угол измеряется половиной дуги, на которую он опирается.
2. Могут ли быть перпендикулярными радиус и хорда, проведённые из одной и той же точки окружности? а) могут, б) не могут.
3. Даны квадрат ОАВС, сторона которого равна 5см, и окружность с центром в точке О радиуса 4см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности? а) ОА и АВ; б) ОА и ВС; в) ВС и АС; г) ОА и АС.
4. Через точку М окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними. а) 45°; б) 30°; в) 90°; г) 60°.
5. Прямая МN касается окружности c центром О радиуса r в точке N. Найдите MN. Если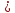 МON =60° , а r = 12cм. а) 12
МON =60° , а r = 12cм. а) 12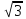 ; б) 12; 6
; б) 12; 6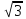 ; г) 24.
; г) 24.
6. Найти вписанный угол АВС, если дуга АС, на которую он опирается, равна 58°. а) 116°; б) 29°; в) 90°; г) 58°.
7. Вписанный угол MNP опирается на дугу MN и равен 46°. Найти градусную меру дуги MN. а) 92°; б) 46°; в) 23°; г) 60°.
8. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 33°. Большая дуга окружности, заключённая между сторонами этого угла, равна 110°. Найти меньшую дугу. а) 22°; б) 11°; в) 44°; г) 33°.
9. Найти острый угол, образованный двумя секущими, проведёнными из точки , лежащей вне окружности, если дуги, заключённые между секущими, равны 130° и 42°. а) 42°; б)21°; в) 44°; г) 22°.
10. Указать верное утверждение а) не в каждый треугольник можно вписать окружность; б) в любой четырёхугольник можно вписать окружность; в) около любого треугольника можно описать окружность; г) если сумма противоположных углов четырёхугольника равна 360°, то около него можно описать окружность.
Тест по теме: «Окружность» 8 класс
2- вариант
1. Выбрать верные утверждения: а) угол с вершиной в центре окружности называется её центральным углом; б) центральный угол измеряется половиной дуги , на которую он опирается; в) угол, вершина, которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом этой окружности; г) вписанный угол измеряется дугой, на которую он опирается.
2.Из одной точки окружности проведены две хорды. Сколько получилось дуг? а) 2; б)4; в) 5; г) 3.
3. Даны квадрат ОАВС, сторона которого равна 7см, и окружность с центром в точке О радиуса 6см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности? а) ОА и АВ; б) ОА и ВС; в) ВС и АС; г) ОА и АС.
4. Через точку В окружности проведены касательная и хорда, равная радиусу окружности. Найдите угол между ними. а) 45°; б) 30°; в) 60°; г) 90°.
5. Прямая МN касается окружности c центром О радиуса r в точке N. Найдите MN. Если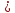 МON = 45° , а r = 8cм. а) 8
МON = 45° , а r = 8cм. а) 8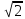 ; б) 4; 4
; б) 4; 4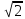 ; г) 8.
; г) 8.
6. Найти вписанный угол АВС, если дуга АС, на которую он опирается, равна 64°. а) 90°; б) 128°; в) 64°; г) 32°.
7. Вписанный угол MNP опирается на дугу MN и равен 52°. Найти градусную меру дуги MN. а) 208°; б) 52°; в) 26°; г) 104°.
8. Через точку, лежащую вне окружности, проведены две секущие, образующие угол в 44°. Большая дуга окружности, заключённая между сторонами этого угла, равна 100°. Найти меньшую дугу. а) 24°; б) 12°; в) 6°; г) 44°.
9. Найти острый угол, образованный двумя секущими, проведёнными из точки , лежащей вне окружности, если дуги, заключённые между секущими, равны 110° и 62°. а) 62°; б)24°; в) 48°; г) 22°.
10. Указать верное утверждение а) в каждый треугольник можно вписать окружность; б) в любой четырёхугольник можно вписать окружность; в) нельзя около любого треугольника описать окружность; г) если сумма противоположных углов четырёхугольника равна 360°, то около него можно описать окружность.
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
,





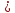 МON =60° , а r = 12cм. а) 12
МON =60° , а r = 12cм. а) 12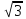 ; б) 12; 6
; б) 12; 6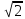 ; б) 4; 4
; б) 4; 4









