МЕТОДИЧЕСКАЯ РАЗРАБОТКА
Тренировочные упражнения по теме «Квадратные уравнения».
Выполнила: учитель математики
МБОУ «СОШ №16» г. Обнинска
Калужской области
Шеханова Наталья Викторовна
2022 г.
Квадратные уравнения - это фундамент, на котором стоит величественное здание алгебры. Умение решать уравнения имеет не только теоретическое значение для познания естественных законов, но и служит практическим целям. Теория уравнений занимает ведущее место в алгебре и математике в целом. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Применяются квадратные уравнения во многих расчетах, сооружениях, спорте, а также вокруг нас.
Именно поэтому важно научить обучающихся решать квадратные уравнения и закрепить данный материал на уроках математики с помощью самостоятельных работ.
Самостоятельная работа важнейшее условие саморегуляции личности, ее творческих возможностей. Самостоятельная работа ученика - главный путь воспитания самостоятельности. Присутствие самостоятельной работы необходимо на уроках, в том числе и на уроках математики, так как они тренируют волю, воспитывают работоспособность, внимание, дисциплинируют учащихся. Учителю на уроках математики необходимо опираться на самостоятельную работу учеников, самостоятельное рассуждение, умозаключение. Можно выделить следующие виды самостоятельных работ на уроках математики:
1.обучающими
2.тренировочными
3.закрепляющими
4.повторительными
5.развивающими
6.творческими
7.контрольными
В своей методической разработке я бы хотела обратить внимание на несколько видов самостоятельных работ- это тренировочные, творческие, контрольные.
Тренировочные самостоятельные работы.
Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и их свойства данного определения, правила.
На мой взгляд по данной теме очень хорошо подходят математические диктанты. Математический диктант - хорошо известное средство обратной связи между учащимися и учителем. Это одна из многих оправдавших себя форм контроля знаний учеников. Математический диктант — короткая письменная самостоятельная работа, во время которой дети воспринимают задание на слух (полностью или частично), решают его или записывают только ответ. Это система связанных между собой вопросов. Продолжительность — 10-15 минут.
На уроках, каждый математический диктант отрабатывает определённые нюансы данной темы и с каждым диктантом задачи усложняются. Диктанты, которые представляю я в своей работе связаны друг с другом (если не отработаны навыки из 1 диктанта, то задания из 2 диктанта выполнить нельзя и т.д.). Задания из данных математических диктантов затем будут включены и в контрольную работу.
Диктант 1. Определить коэффициенты и вид уравнения (позволяет отработать понятие полное, неполное квадратное уравнение и легко ориентироваться в коэффициентах уравнения).
(Здесь и в дальнейшем в квадратных скобках указаны задания для второго варианта)
Записать коэффициенты и определить вид уравнения:
-
-9+5х2 =0 [-11+12 х2=0]
-
6 х2-х=0 [-5 х2+2x=0]
-
6x-3-12 х2=0 [x-5-10х2=0]
-
-13x+9 х2=0 [5x-48 х2=0]
-
2-8х2-0,5x=0 [ 0,3- 3x2+4x=0]
-
25 х2=0 [13x2=0]
-
-4+3x- х2 =0 [-1+2x+ х2=0]
-
6 х2+3x+9=0 [7x2-5x+2=0]
-
-5x2+2x+4=0 [-10x2+16x-12=0]
-
17x-x2=0 [30x-3x2=0]
-
2x2-11=0[x2+10=0]
Диктант 2. Восстановить квадратные уравнения по заданным значениям коэффициентов и определить его вид. (позволяет по заданным коэффициентам определять вид квадратного уравнения и составлять его).
Определите вид квадратного уравнения и составьте его:
-
а=1, в=2, с=0 [а=3, в=0, с=4]
-
а=3, в=-22, с=1 [а=-3, в=7, с=12]
-
а=1, в=2, с=0 [а=3, в=0, с=4]
-
а=-5, в=0, с=0 [а=13, в=-7, с=0]
-
а=-4, в=-1, с=-5 [а=-9, в=23, с=-11]
-
а=-6, в=0, с=-2,5 [а=4, в=-9, с=0]
-
а=1, в=-4, с=+3 [а=1, в=-6, с=5]
-
а=7, в=-1, с=-8 [а=6, в=1, с=-7]
-
а=2, в=0, с=-50 [а=3, в=0, с=-48].
Диктант 3. Приведение уравнения к стандартному виду. (отрабатывает навык приведения уравнения к стандартному виду, а также идет отработка понятия стандартного вида и подводит детей к следующей работе по нахождению дискриминанта).
Приведите уравнение к стандартному виду:
-
2х2+1=5х [х2=5х-76]
-
15х+9=-3х2 [6-2х=3х2]
-
-7=-5х2-х [-2=6х-8х2]
-
18х=7-х2 [-3х=5-7х2]
-
2=4х2+х [4=6х2-х]
-
4х+х2+5=0 [-2х+х2+3=0]
-
х2+2х-2=-2[х2-2х-3=3]
-
25х2=1 [4=24х2]
Диктант 4. Решение не полного квадратного уравнения (позволяет проверить освоение навыков решения неполных квадратных уравнений)
Решите уравнения:
-
3х2-12=0 [7х2-14=0]
-
1,8х2=0 [4,9х2=0]
-
15-5х2=0 [-25+4х2=0]
-
х2=3х [2х2=-6х]
-
-0,2х2+4=0 [3-0,4х2=0]
-
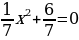
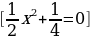
Диктант 5. Вычисление дискриминанта и определение количества корней (отработка навыка нахождение дискриминанта, как когда известны только коэффициенты, так и когда дано полное уравнение, умение определять сколько корней будет в уравнении.)
Вычислите дискриминант и определите количество корней уравнения:
-
а=7, в=2, с=4 [а=-3, в=7, с=12]
-
а=1, в=-2, с=1 [а=1, в=-4, с=4]
-
х2-7х+10=0 [х2-5х+6=0]
-
-t2-3t+1=0 [-t2+t+3=0]
-
3х2+х=4 [2х2-х=3]
-
-а2-5а+14=0 [-а2-26а-25=0]
-
6х+9=х2 [х2 =4х-29]
Диктант 6. Решение уравнений через формулу корней. (отработка формулы корней квадратного уравнения).
Решите уравнения:
-
2х2-3х+2=0 [7х2+8х+1=0]
-
х2+7х-44=0 [х2-10х-39=0]
-
2х2+7х-9=0 [3х2+13х-10=0]
-
х2-16х+63=0 [х2-2х-35=0]
-
7х2-х-8=0 [6х2+х-7=0]
-
2х2-5х+1=-1[2х2-3х-1=1]
Диктант 7. Решение квадратных уравнений с четным вторым коэффициентом (Д1).
(отработка решения квадратного уравнения вида ах2+2кх+с=0. 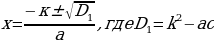
Решите уравнение через Д1:
-
9х2-14х+5=0 [9у2-30у+25=0]
-
1-18р+81р2=0 [5у2-6у+1=0]
-
х2+22х-23=0 [у2-10у-25=0]
-
4х2+4х+1=0 [8у2-14у+5=0]
-
36х2-12х+1=0 [100у2-160у+63=0]
-
Х2-20х=20х+100 [3у2=10-29у]
Диктант 8. Решение уравнений через свойства коэффициентов квадратного уравнения (отработка навыков применения свойств коэффициентов квадратного уравнения. Если а+в+с=0, то х1=1, х2=с/а. Если а-в+с=0, то х1=-1, х2=-с/а. Позволяет быстро находить корни уравнения с большими коэффициентами).
Решите квадратное уравнение применяя свойства коэффициентов:
-
х2+17х-18=0 [3х2+4х-1=0]
-
х2-39х-40=0 [х2-29х-30=0]
-
2х2-х-3=0 [7х2+2х-5=0]
-
13х2-18х+5=0 [14х2-17х+3=0]
-
200х2-87х-287=0 [100х2-97х-197=0]
Диктант 9. Решение уравнений с помощью теоремы Виета (отработка понятия приведенное квадратное уравнение, уравнение вида х2+рх+q=0, отработка применения данной теоремы к решению уравнений, применение теоремы обратной теореме Виета. Применение данной теоремы позволяет обучающимся быстро делать проверку правильности решения квадратного уравнения).
-
Найдите сумму и произведение корней:
-
х2-37х+27=0 [2у2-9у-10=0]
-
х2-16х+28=0 [у2-12у-45=0]
-
х2-27х=0 [у2-12=0]
-
Найдите корни уравнений по теореме Вите:
-
х2-9х+20=0 [у2+11у-12=0]
-
х2+17х-38=0 [7у2-11у-6=0]
Диктант 10. Закрепление изученного материала ( теоретический). (позволяет повторить пройденный материал и подготовиться к последующей контрольной работе)
-
Является ли уравнение х2-7х+10=0 [х2-5х=0] полным?
-
Какое число в уравнении является свободным членом 4х+х2+5=0 [-2х+х2+3=0]?
-
Является ли уравнение приведенным 4х+х2+5=0 [-2х+х2+3=0]?
-
Является ли число 0 корнем уравнения -8х2-0,5x=0 [ 0,3- 3x2=0]?
-
Может ли квадратное уравнение не иметь корней [иметь один корень]? Если да, то при каком условии?
-
Верно ли что 0 [1] является корнем любого квадратного уравнения?
-
Каков стандартный вид квадратного уравнения? [уравнения которое можно решить через Д1]?
-
Чему равны корни квадратного уравнения, если выполняется равенство а-в+с=0 [а+в+с=0]?
-
Для каких квадратных уравнений работает теорема Виета?
Творческие самостоятельные работы.
Большой интерес у учащихся вызывают творческие самостоятельные работы, которые предполагают высокий уровень самостоятельности. С большим удовольствием обучающиеся выполняют такие работы по теме квадратные уравнения, где надо решить данное уравнение и по полученным корням сделать рисунки.
Карточки можно использовать как для индивидуальной работы, так же и для парной и групповой работы.
Карточка 1.
Соедините последовательно точки с координатами (х1; х2), а для выделенных уравнений
(х2; х1), где х1- меньший корень, х2- больший корень уравнения. (Карточка представлена в виде таблицы где 3 столбик учащиеся должны заполнить сами).
| № | Уравнения | Координаты точки |
| 1 | х2-7х=0 |
|
| 2 | х2-6х-27=0 |
|
| 3 | х2-3х-54=0 |
|
| 4 | х2+3х-54=0 |
|
| 5 | х2+7х-18=0 |
|
| 6 | х2+9х+18=0 |
|
| 7 | х2+9х=0 |
|
| 8 | х2-3х-18=0 |
|
| 9 | х2-11х+18=0 |
|
| 10 | х2-15х+54=0 |
|
| 11 | х2-15х+54=0 |
|
| 12 | х2-12х+27=0 |
|
| 13 | х2-7х=0 |
|
Ответ:
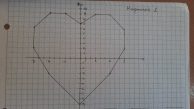
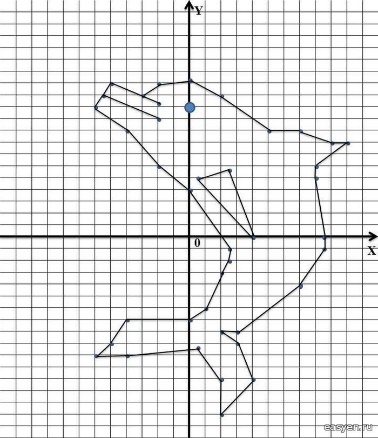
Карточка 2.
Соедините последовательно точки с координатами (х1; х2), а для выделенных уравнений
(х2; х1), где х1- меньший корень, х2- больший корень уравнения. (Карточка представлена в виде таблицы где 3 столбик учащиеся должны заполнить сами).
| № | Уравнения | Координаты точки |
| 1 | х2+3х-4=0 |
|
| 2 | 2х2+10х-12=0 |
|
| 3 | -х2-4х+12=0 |
|
| 4 | х2-2х-15=0 |
|
| 5 | х2-10х+21=0 |
|
| 6 | -2х2+12х-10=0 |
|
| 7 | х2-6х+8=0 |
|
| 8 | -х2+7х=12 |
|
| 9 | 0,5х2-3,5х+5=0 |
|
| 10 | х2-4х=4х-12 |
|
| 11 | -2х2+24х-64=0 |
|
| 12 | -7х+х2-8=0 |
|
| 13 | 2х2 -12х=0 |
|
| 14 | х2=-3х |
|
| 15 | 0,25х2+х-3=0 |
|
| 16 | -5х=х2+6х |
|
| 17 | х(х+6)=-8 |
|
| 18 | (х+5)(х+1)=0 |
|
| 19 | х2+5х-6=0 |
|
| 20 | х2=2х+15 |
|
| 21 | х2-4=0 |
|
| 22 | 2х=-х2 |
|
| 23 | -4х2-24х-32=0 |
|
| Глаз |
| 1 | х2+х-12=0 |
|
Ответ:
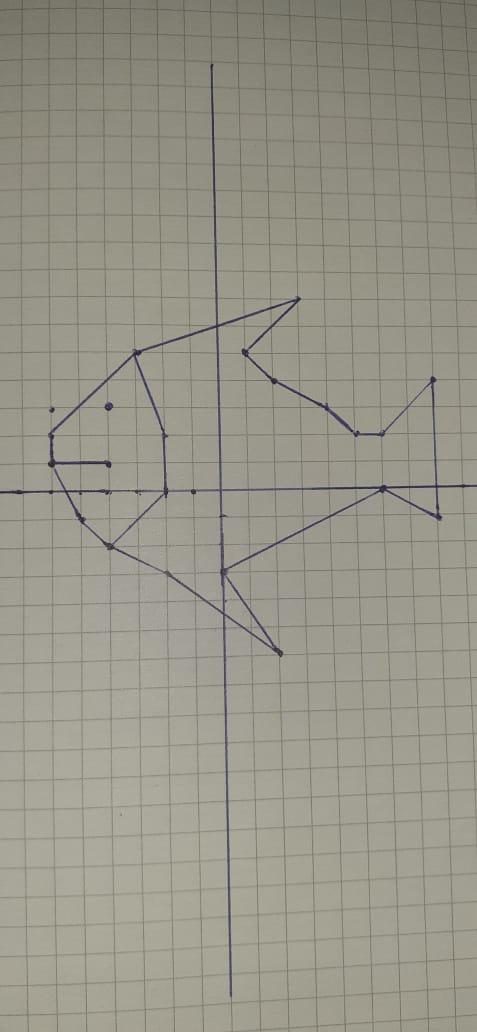
Карточка 3.
Соедините последовательно точки с координатами (х1; х2), а для выделенных уравнений
(х2; х1), где х1- меньший корень, х2- больший корень уравнения. (Карточка представлена в виде таблицы где 3 столбик учащиеся должны заполнить сами).
| № | Уравнения | Координаты точки |
| 1 | x2+6x+9=0 |
|
| 2 | x2-5x=0 |
|
| 3 | x2-10x+21=0 |
|
| 4 | x2-12x+36=0 |
|
| 5 | x2-12x+20=0 |
|
| 6 | x2-8x-33=0 |
|
| 7 | x2-6x-7=0 |
|
| 8 | x2-3x=0 |
|
| 9 | x2+x=0 |
|
| 10 | x2+6x+9=0 |
|
| 11 | x2-6x-27=0 |
|
| 12 | x2+2x-35=0 |
|
| 13 | x2+14x+49=0 |
|
| 14 | x2+12x+27=0 |
|
| 15 | x2+6x+9=0 |
|
| 16 | x2-15x-54=0 |
|
| 17 | x2-13x=0 |
|
| 18 | x2-11x-42=0 |
|
Ответ:
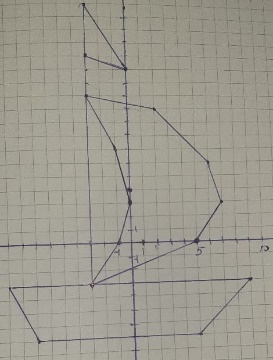
Карточка 4. По данному рисунку и координатам точек задать соответствующие уравнения (точки с координатами (х1; х2), выделить уравнения, в которых координаты (х2; х1), где х1- меньший корень, х2- больший корень уравнения.) (В данном задании учащиеся должны заполнить всю таблицу самостоятельно, можно давать как индивидуально, так и в группах).
| № | Уравнения | Координаты точки |
| 1 |
|
|
| 2 |
|
|
Карточка 5. (данную работу можно делать как индивидуально, так и в парах, и в группах. Она развивает не только способность решать квадратные уравнения, но и внимательность). (В ответе получится: Я вас люблю).

Контрольная работа.
Контрольные работы являются необходимым условием достижения планируемых результатов обучения.
Контрольные задания должны быть равноценными по содержанию и объему работы; должны быть направлены на отработку основных навыков; обеспечивать достоверную проверку уровня обучения; они должны стимулировать учащихся; позволять им продемонстрировать прогресс в своей общей подготовке.
Данная контрольная работа составлена на основании тех математических диктантов и творческих работ, которые были представлены выше.
Контрольная работа составлена в трех вариантах, различающихся по уровню сложности заданий.
Вариант 1 рассчитан на слабо подготовленных учащихся. Он ориентирован в основном на достижение учащимися обязательного уровня математической подготовки, определенного стандартом математического образования. Для многих заданий здесь даются ответы, указания, пошаговые инструкции, некоторые данные для самоконтроля.
Вариант 2 усложнен по сравнению с вариантом 1. Он не только способствует достижению учащимися обязательного уровня математической подготовки, но и создает условия для овладения алгебраическими знаниями и умениями на более высоком уровне.
Вариант 1.
№1. Для каждого вида уравнения ax2 + bx +c =0 укажите значения a, b, c:
-
-4+3x- х2 =0;
-
6 х2+3x+9=0;
-
17x-x2=0;
-
2x2-11=0.
№2. Вычислите дискриминант D квадратного уравнения ax2 + bx +c =0 по формуле
D = b2 – 4ac, и определить количество корней:
-
х2-7х+10=0;
-
2х2-5х+6=0.
№3 Решите уравнения:
-
х2-16х+63=0;
-
х2-2х-35=0;
-
7х2-х-8=0;
-
6х2+х-7=0.
Вариант 2.
№1. Для каждого вида уравнения ax2 + bx +c =0 укажите значения a, b, c :
-
у2-12у-45=0;
-
х2-27х=0;
-
у2-12=0.
№2. Найти дискриминант:
-
х2+17х-38=0;
-
у2-у-930=0.
№3 Решите уравнения:
-
4х2+4х+1=0;
-
8у2-14у+5=0;
-
36х2-12х+1=0;
-
100у2-160у+63=0.
№4. Найдите корни уравнения:
а) 4х (х - 1) + х (х + 2) = 0
в) 2(х2 – 1) = 3 – х(2х +1)
б) 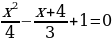
№5. При каких значениях х значение трехчлена х2 + 14х + 10 равно - 14.
Дополнительно можно дать задания для тех, кто увлекается математикой, так называемые «Для любознательных». Подпитывая интерес учащихся к решению таких задач, подбираю задачи с познавательным содержанием, с исследовательской деятельностью со стороны ребят, с поиском.
Здесь встречаются задания, требующие не только свободного владения приобретенными знаниями, но и творческого подхода, проявления смекалки и сообразительности.
1. Вычислите дискриминант D квадратного уравнения и укажите число его корней:
а) 6х2 +11х – 2 = 0; б) 36 х2 + 12 х + 1 = 0; в) 3 х2 + 2 х + 4 = 0.
2. При каких значениях b имеет единственный корень уравнение:
а) 4х2 - bх + 4 = 0; б) bх2 + 12х - 4 = 0.
3. При каких значениях m уравнение (m + 4)х2 – 8х + m – 11 = 0 имеет единственный
корень?
4. Решите уравнение:
а) 6х2 - 5х + 1 = 0; б) х2 + 3 х + 2,25 = 0;
в) х2 - 4√2 х + 4 = 0; г) х2 + 4√2 х - 10 = 0
Ответ: в) 2√2 – 2 и 2√2 + 2; г) - 5√2 и √2.
5. Найдите корни уравнения:
а) х(х – 10) – х(1,2 – х) + 12,8 = 0; б) (х2 -1)/4 = 3(3х + 1)/8 – 1,75
6. При каких значениях b трехчлен 6 b2 - 6b + 3 и двучлен b2 + 2b принимают равные
значения, и какие именно?