Тренировочный вариант 2

Единый государственный экзамен, 2021 г.

МАТЕМАТИКА. Профильный уровень

Тренировочный вариант №2 от 14.09.2020

3 / 10

Ответом к заданиям 1–12 является целое число или конечная десятичная дробь. Запишите число в поле ответа в тексте работы, затем перенесите его в БЛАНК ОТВЕТОВ № 1 справа от номера соответствующего задания, начиная с первой клеточки. Каждую цифру, знак «минус» и запятую пишите в отдельной клеточке в соответствии с приведёнными в бланке образцами. Единицы измерений писать не нужно.

ТРЕНИРОВОЧНЫЙ КИМ № 200914

Единый государственный экзамен по МАТЕМАТИКЕ

Профильный уровень Инструкция по выполнению работы

Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий с кратким ответом базового уровня сложности. Часть 2 содержит 4 задания с кратким ответом повышенного уровня сложности и 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.

Все бланки ЕГЭ заполняются яркими чёрными чернилами.

Допускается использование гелевой или капиллярной ручки.

При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

После завершения работы проверьте, что ответ на каждое задание в бланках ответов №1 и №2 записан под правильным номером.

Желаем успеха!

Справочные материалы

sin² 𝛼 + cos² 𝛼 = 1 sin 2𝛼 = 2 sin 𝛼 ⋅ cos 𝛼

cos 2𝛼 = cos² 𝛼 − sin² 𝛼

sin⁽𝛼 + 𝛽⁾ = sin 𝛼 ⋅ cos 𝛽 + cos 𝛼 ⋅ sin 𝛽 cos⁽𝛼 + 𝛽⁾ = cos 𝛼 ⋅ cos 𝛽 − sin 𝛼 ⋅ sin 𝛽

Часть 1

1

В книге Елены Молоховец «Подарок молодым хозяйкам» имеется рецепт пирога с черносливом. Для пирога на 10 человек следует взять ⁵ фунта

9

чернослива. Сколько граммов чернослива следует взять для пирога,

рассчитанного на 9 человек? Считайте, что 1 фунт равен 0,4 кг. Ответ: .

2

На рисунке жирными точками показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наименьшую среднемесячную температуру в период с мая по декабрь 1920 года включительно. Ответ дайте в градусах Цельсия.

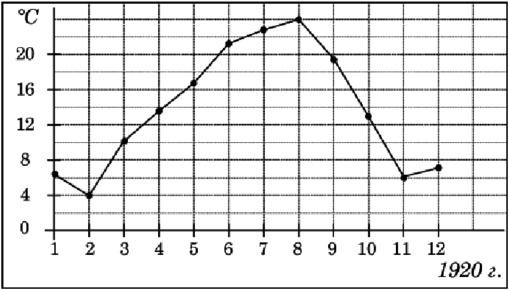
Ответ: .

3

На клетчатой бумаге с размером клетки 1 × 1 изображён угол. Найдите тангенс этого угла.

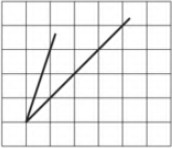
Ответ: .

4

В чемпионате мира участвуют 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Китая окажется в четвёртой группе?

Ответ: .

5

Найдите корень уравнения

𝑥² − 8 = ⁽𝑥 − 4⁾².

Ответ: .

В треугольнике 𝐴𝐵𝐶 угол 𝐴 равен 60°, угол 𝐵 равен 53°. 𝐴𝐷, 𝐵𝐸 и 𝐶𝐹 − биссектрисы, пересекающиеся в точке 𝑂. Найдите угол 𝐴𝑂𝐹. Ответ дайте в градусах.

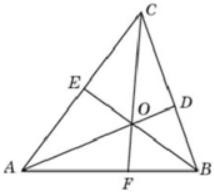
6

ТРЕНИРОВОЧНЫЙ КИМ № 200914

Ответ: .

7

На рисунке изображен график функции 𝑦 = 𝑓⁽𝑥⁾, определенной на интервале ⁽−2; 12⁾. Найдите сумму точек экстремума функции 𝑓⁽𝑥⁾.

Ответ: .

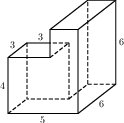
8

Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

В боковой стенке высокого цилиндрического бака у самого дна закреплён кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нём, выраженная в метрах, меняется по закону

10

𝐻⁽𝑡⁾

^{= 𝐻0 −} √^{2𝑔𝐻0𝑘𝑡 +}

^𝑔 _𝑘2_𝑡2 2

, где 𝑡 — время в секундах, прошедшее с

момента открытия крана, 𝐻₀ = 5 м — начальная высота столба воды,

𝑘 = ¹

200

— отношение площадей поперечных сечений крана и бака, а 𝑔 —

ускорение свободного падения (считайте 𝑔 = 10 м/с²). Через сколько секунд после открытия крана в баке останется четверть первоначального объёма воды?

Ответ: .

Не забудьте перенести все ответы в бланк ответов № 1.

Ответ: .

Часть 2

9

Найдите значение выражения

⁽16𝑥² + 9𝑦² − ⁽4𝑥 − 3𝑦⁾²⁾: (−6𝑥𝑦).

Ответ: .

Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 150 метрам?

11

Ответ: .

12

Найдите наименьшее значение функции

3

𝑦 = 𝑥² − 27𝑥 + 6 на отрезке ^[1; 422^].

Ответ: .

ТРЕНИРОВОЧНЫЙ КИМ № 200914

13

а) Решите уравнение

19 ∙ 4^𝑥 − 5 ∙ 2^𝑥+2 + 1 = 0.

б) Найдите все корни этого уравнения, принадлежащие отрезку ^[−5; −4^].

14

В правильной треугольной призме 𝐴𝐵𝐶𝐴₁𝐵₁𝐶₁ стороны основания равны 20,

боковые рёбра равны 11.

а) Докажите, что сечение призмы плоскостью, проходящей через 𝐴₁, 𝐵₁ и середину ребра 𝐵𝐶, является трапецией.

б) Найдите площадь сечения призмы плоскостью, проходящей через вершины 𝐴₁, 𝐵₁ и середину ребра 𝐵𝐶.

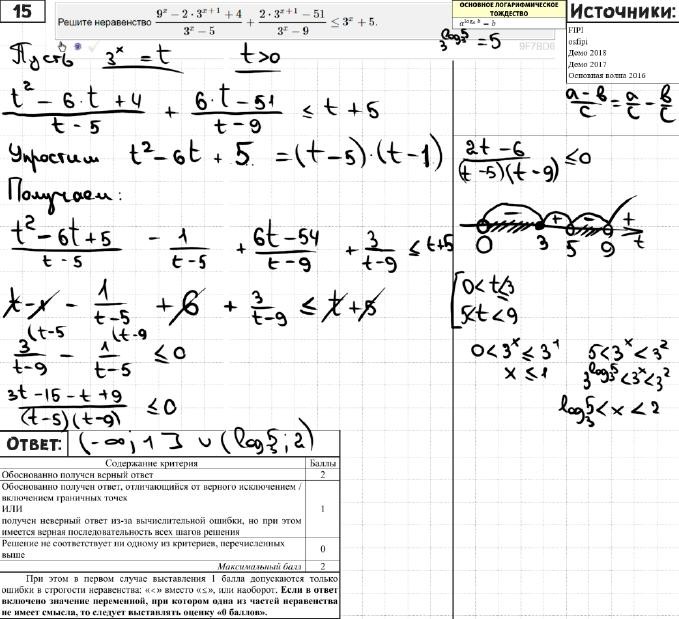
15

Решите неравенство

31 декабря 2014 года Пётр взял в банке некоторую сумму в кредит под некоторый процент годовых. Схема выплаты кредита следующая – 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 𝑎%), затем Пётр переводит очередной транш. Если он будет платить каждый год по 2 592 000 рублей, то выплатит долг за 4 года. Если по 4 392 000 рублей, то за 2 года. Под какой процент Пётр взял деньги в банке?

18

17

ТРЕНИРОВОЧНЫЙ КИМ № 200914

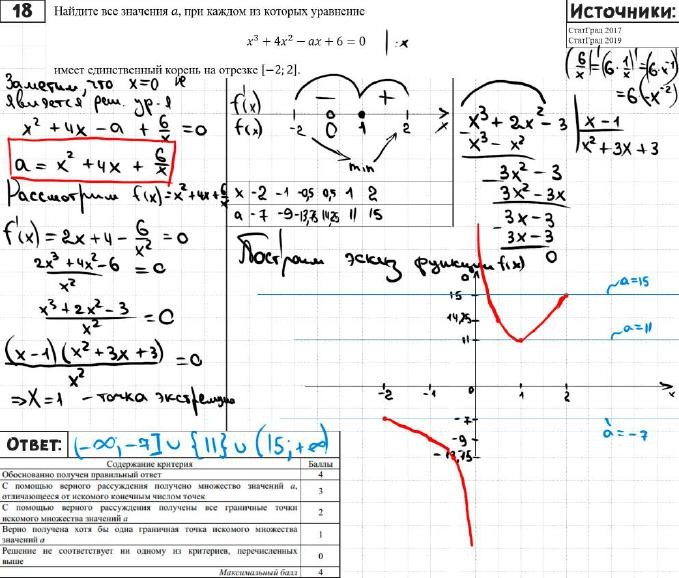
Найдите все значения 𝑎, при каждом из которых уравнение

𝑥³ + 4𝑥² − 𝑎𝑥 + 6 = 0

имеет единственный корень на отрезке ^[−2; 2^].

19

На доске было написано 30 натуральных чисел (необязательно различных), каждое из которых не превосходит 40. Среднее арифметическое написанных чисел равнялось 7. Вместо каждого из чисел на доске написали число, в два раза меньшее первоначального. Числа, которые после этого оказались меньше 1, с доски стёрли.

а) Могло ли оказаться так, что среднее арифметическое чисел, оставшихся

9^𝑥 − 2 ∙ 3^𝑥+1 + 4

3^𝑥 − 5 ⁺

2 ∙ 3^𝑥+1 − 51

3^𝑥 − 9

≤ 3^𝑥 + 5.

на доске, больше 14?

б) Могло ли среднее арифметическое оставшихся на доске чисел оказаться больше 12, но меньше 13?

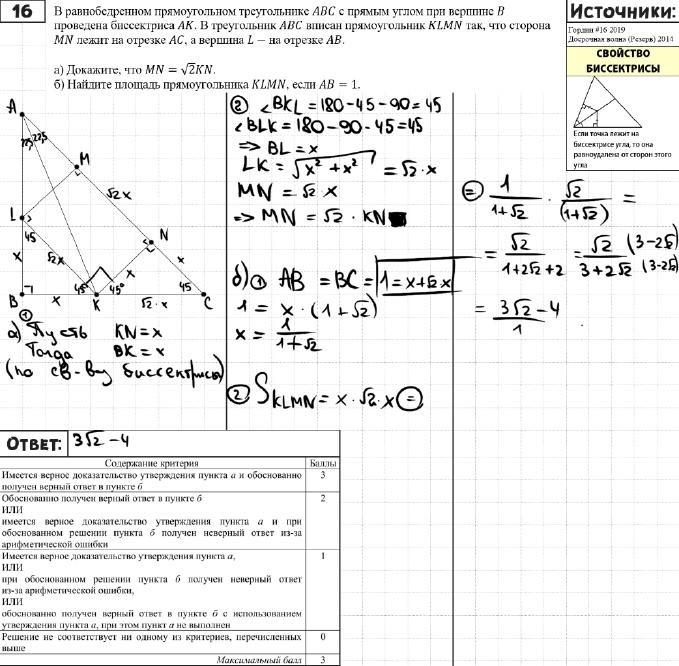
16

В равнобедренном прямоугольном треугольнике 𝐴𝐵𝐶 с прямым углом при вершине 𝐵 проведена биссектриса 𝐴𝐾. В треугольник 𝐴𝐵𝐶 вписан прямоугольник 𝐾𝐿𝑀𝑁 так, что сторона 𝑀𝑁 лежит на отрезке 𝐴𝐶, а вершина

𝐿 − на отрезке 𝐴𝐵.

^{а) Докажите, что 𝑀𝑁 =} √^2𝐾𝑁.

б) Найдите площадь прямоугольника 𝐾𝐿𝑀𝑁, если 𝐴𝐵 = 1.

в) Найдите наибольшее возможное значение среднего арифметического чисел, которые остались на доске.

Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.

О проекте «Пробный ЕГЭ каждую неделю»

Данный ким составлен командой всероссийского волонтёрского проекта

«ЕГЭ 100 баллов» https://vk.com/ege100ballov и безвозмездно распространяется для любых некоммерческих образовательных целей.

Нашли ошибку в варианте?

Напишите нам, пожалуйста, и мы обязательно её исправим!

Для замечаний и пожеланий: https://vk.com/topic-10175642_41259310

(также доступны другие варианты для скачивания)

ТРЕНИРОВОЧНЫЙ КИМ № 200914

Система оценивания экзаменационной работы по математике (профильный уровень)

СОСТАВИТЕЛЬ ВАРИАНТА:
ФИО:	Евгений Пифагор
Предмет:	Математика
Стаж:	10-й год готовлю к ЕГЭ
Регалии:	Набрал 98 баллов на ЕГЭ по математике (профиль) 20 учеников набрали 90-99 баллов на ЕГЭ 2020 Высшее образование (ТГУ, 2009-2014) Победитель трёх олимпиад по высшей математике
Аккаунт и группа ВК:	https://vk.com/eugene10 https://vk.com/shkolapifagora
Ютуб и инстаграм:	https://youtube.com/c/pifagor1 https://instagram.com/shkola_pifagora

Номер задания	Правильный ответ	Видео решение
1	200
2	6
3	0,5
4	0,2
5	3
6	63,5
7	44
8	108
9	-4
10	100
11	6
12	-2910
13	а) 0; − log2 19 б) − log2 19
14	210
15	(−∞; 1] 𝖴 (log3 5 ; 2)
16	3√2 − 4
17	20
18	(−∞; −7] 𝖴 {11} 𝖴 (15; +∞)
19	а) да, 25×1, 5×37 б) нет в) 18,5

Каждое из заданий 1–12 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.

ТРЕНИРОВОЧНЫЙ КИМ № 200914

Решения и критерии оценивания заданий 13–19

Количество баллов, выставленных за выполнение заданий 13–19, зависит от полноты решения и правильности ответа.

Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.

Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.

При выполнении задания могут использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.

ТРЕНИРОВОЧНЫЙ КИМ № 200914

ТРЕНИРОВОЧНЫЙ КИМ № 200914

ТРЕНИРОВОЧНЫЙ КИМ № 200914

ТРЕНИРОВОЧНЫЙ КИМ № 200914

В соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам среднего общего образования (приказ Минпросвещения России и Рособрнадзора от 07.11.2018 № 190/1512, зарегистрирован Минюстом России 10.12.2018 № 52952)

«82. По результатам первой и второй проверок эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы ЕГЭ с развернутым ответом.

В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.

Эксперту, осуществляющему третью проверку, предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу».

Существенными считаются следующие расхождения:

1. расхождение в баллах, выставленных двумя экспертами за выполнение любого из заданий 13–19, составляет 2 или более балла. В этом случае третий эксперт проверяет только ответ на то задание, который был оценен двумя экспертами со столь существенным расхождением;

2. расхождения экспертов при оценивании ответов на хотя бы два из заданий 13–19. В этом случае третий эксперт проверяет ответы на все задания работы.

© 2020 Всероссийский проект «ЕГЭ 100БАЛЛОВ» vk.com/ege100ballov

Составитель: Школа Пифагора

Обсуждение заданий: https://vk.com/topic-40390806_40779359

Разрешается свободное копирование в некоммерческих образовательных целях