Россия, Уфа
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 07.12.2021 09:45
Чугаева Олеся Алексеевна
Директор МБОУ "ЦО № 76", учитель математики
44 года
769
71 652 
Местоположение
Специализация
Тренировочный вариант 6
Категория:
Математика
02.12.2021 12:44
Просмотр содержимого документа
«Тренировочный вариант 6»
ТРЕНИРОВОЧНЫЙ КИМ № 201012
Единый государственный экзамен, 2021 г. МАТЕМАТИКА. Профильный уровень Тренировочный вариант №6 от 12.10.2020 1 / 10
© 2020 Всероссийский проект «ЕГЭ 100БАЛЛОВ» vk.com/ege100ballov
Составитель: Школа Пифагора
Обсуждение заданий: https://vk.com/topic-40390806_40779359
Разрешается свободное копирование в некоммерческих образовательных целях
ТРЕНИРОВОЧНЫЙ КИМ № 201012
Единый государственный экзамен, 2021 г. МАТЕМАТИКА. Профильный уровень Тренировочный вариант №6 от 12.10.2020 2 / 10
© 2020 Всероссийский проект «ЕГЭ 100БАЛЛОВ» vk.com/ege100ballov
Составитель: Школа Пифагора
Обсуждение заданий: https://vk.com/topic-40390806_40779359
Разрешается свободное копирование в некоммерческих образовательных целях
Единый государственный экзамен, 2021 г. МАТЕМАТИКА. Профильный уровень Тренировочный вариант №6 от 12.10.2020 3 / 10
10
8
ТРЕНИРОВОЧНЫЙ КИМ № 201012
Площадь поверхности тетраэдра равна 12. Найдите площадь поверхности Коэффициент полезного действия (КПД) некоторого двигателя многогранника, вершинами которого являются середины ребер данного тетраэдра.
определяется формулой 𝜂 = 𝑇1−𝑇2 ∙ 100%, где 𝑇
𝑇1 1
— температура нагревателя
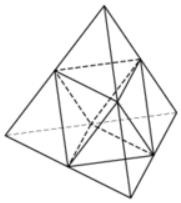
Ответ: .
(в кельвинах), 𝑇2 — температура холодильника (в кельвинах). При какой
температуре нагревателя 𝑇1 КПД этого двигателя будет 25%, если температура холодильника 𝑇2 = 276 К? Ответ дайте в градусах Кельвина.
Ответ: .
Первый садовый насос перекачивает 8 литров воды за 2 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 36 литров воды?
Ответ: .
9
Найдите значение выражения
Найдите точку минимума функции
𝑦 = (𝑥2 − 17𝑥 + 17) ∙ 𝑒7−𝑥.
Ответ: .
5(𝑝(2𝑥) − 2𝑝(𝑥 + 5)), если 𝑝(𝑥) = 𝑥 − 10.
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы.
Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
Ответ: .
13
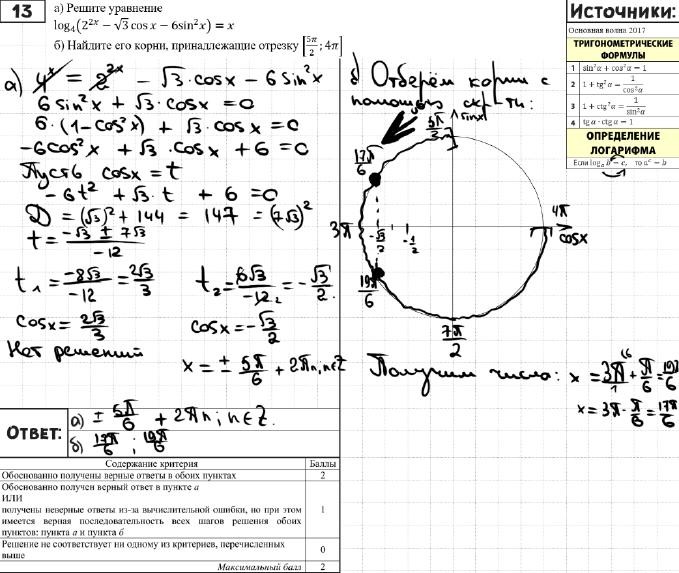
а) Решите уравнение
log4(22𝑥 − √3 cos 𝑥 − 6sin2𝑥) = 𝑥.
б) Найдите все корни этого уравнения, принадлежащие отрезку
5𝜋
[ ; 4𝜋]. 2
14
Дана треугольная призма 𝐴𝐵𝐶𝐴1𝐵1𝐶1. Плоскость 𝛼 проходит через прямую𝐵𝐶1 параллельно прямой 𝐴𝐵1.
а) Докажите, что плоскость 𝛼 проходит через середину ребра 𝐴𝐶.
б) Найдите площадь сечения призмы плоскостью 𝛼, если призма правильная, сторона её основания равна 2√3, а боковое ребро равно 1.
15
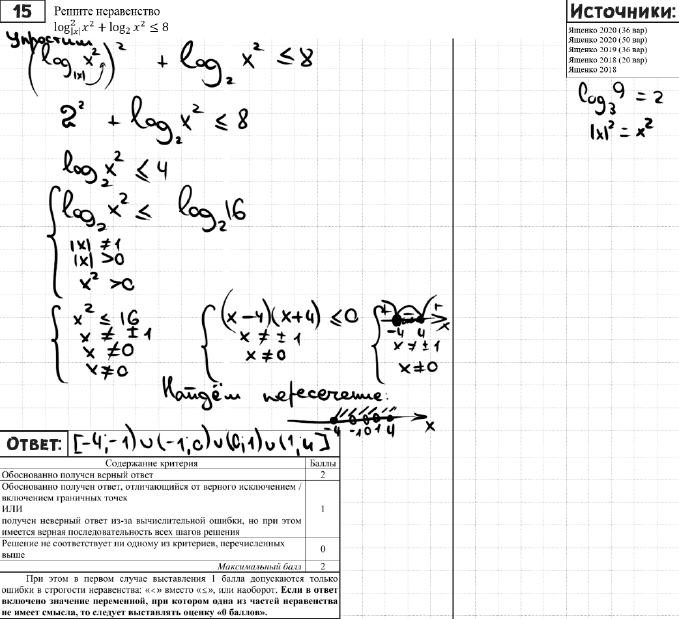
Решите неравенство
|𝑥|
log2 𝑥2 + log2 𝑥2 ≤ 8.
16
В равнобедренную трапецию 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 вписана окружность, 𝐶𝐻 − высота трапеции.а) Докажите, что центр окружности, вписанной в трапецию, лежит на отрезке 𝐵𝐻.
б) Найдите диагональ 𝐴𝐶, если средняя линия трапеции равна 2√7, а
∠𝐴𝑂𝐷 = 120°, где 𝑂 − центр окружности, вписанной в трапецию, а 𝐴𝐷 −
большее основание.
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование.
17
ТРЕНИРОВОЧНЫЙ КИМ № 201012
В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно 𝑡2 часов в неделю, то за эту неделю они производят 3𝑡 единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно 𝑡2 часов в неделю, то за эту неделю они производят 5𝑡 единиц товара.За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей.
Григорий готов выделять 6 800 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Найдите наименьшее значение параметра 𝑎, для которого существует хотя бы одна пара (𝑥; 𝑦) таких чисел 𝑥 и 𝑦, что
𝑥2 + 2𝑦2 − 𝑥𝑦 − 𝑎𝑥 + 𝑎𝑦 + 𝑎2 ≤ 1.
а) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа.
б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа?
в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа.
Проверьте, чтобы каждый ответ был записан рядом с номером соответствующего задания.
О проекте «Пробный ЕГЭ каждую неделю»
Данный ким составлен командой всероссийского волонтёрского проекта
«ЕГЭ 100 баллов» https://vk.com/ege100ballov и безвозмездно распространяется для любых некоммерческих образовательных целей.
Нашли ошибку в варианте?
Напишите нам, пожалуйста, и мы обязательно её исправим!
Для замечаний и пожеланий: https://vk.com/topic-10175642_41259310
(также доступны другие варианты для скачивания)
ТРЕНИРОВОЧНЫЙ КИМ № 201012
Система оценивания экзаменационной работы по математике (профильный уровень)
|
СОСТАВИТЕЛЬ ВАРИАНТА: | |
| ФИО: | Евгений Пифагор |
| Предмет: | Математика |
| Стаж: | 10-й год готовлю к ЕГЭ |
|
Регалии: | Набрал 98 баллов на ЕГЭ по математике (профиль) 20 учеников набрали 90-99 баллов на ЕГЭ 2020 Высшее образование (ТГУ, 2009-2014) Победитель трёх олимпиад по высшей математике |
| Аккаунт и группа ВК: | https://vk.com/eugene10 https://vk.com/shkolapifagora |
| Ютуб и инстаграм: | https://youtube.com/c/pifagor1 https://instagram.com/shkola_pifagora |
| Номер задания | Правильный ответ | Видео решение |
| 1 | 30 |
|
| 2 | 72 |
|
| 3 | 96 |
|
| 4 | 0,68 |
|
| 5 | -0,75 |
|
| 6 | 12,5 |
|
| 7 | 7 |
|
| 8 | 6 |
|
| 9 | 0 |
|
| 10 | 368 |
|
| 11 | 7 |
|
| 12 | 2 |
|
|
13 | 5𝜋 а) ± + 2𝜋𝑛; 𝑛 ∈ 𝑍 6 17𝜋 19𝜋 б) ; 6 6 |
|
| 14 | 3 |
|
| 15 | [−4; −1) 𝖴 (−1; 0) 𝖴 (0; 1) 𝖴 (1; 4] |
|
| 16 | 7 |
|
| 17 | 680 |
|
| 18 | −√1,4 |
|
|
19 | а) 2592 б) нет в) все комбинации цифр 5568 |
|
Каждое из заданий 1–12 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.
ТРЕНИРОВОЧНЫЙ КИМ № 201012
Решения и критерии оценивания заданий 13–19
Количество баллов, выставленных за выполнение заданий 13–19, зависит от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.При выполнении задания могут использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.
ТРЕНИРОВОЧНЫЙ КИМ № 201012
ТРЕНИРОВОЧНЫЙ КИМ № 201012
ТРЕНИРОВОЧНЫЙ КИМ № 201012
ТРЕНИРОВОЧНЫЙ КИМ № 201012
В соответствии с Порядком проведения государственной итоговой аттестации по образовательным программам среднего общего образования (приказ Минпросвещения России и Рособрнадзора от 07.11.2018 № 190/1512, зарегистрирован Минюстом России 10.12.2018 № 52952)«82. По результатам первой и второй проверок эксперты независимо друг от друга выставляют баллы за каждый ответ на задания экзаменационной работы ЕГЭ с развернутым ответом.
В случае существенного расхождения в баллах, выставленных двумя экспертами, назначается третья проверка. Существенное расхождение в баллах определено в критериях оценивания по соответствующему учебному предмету.
Эксперту, осуществляющему третью проверку, предоставляется информация о баллах, выставленных экспертами, ранее проверявшими экзаменационную работу».
Существенными считаются следующие расхождения:
-
расхождение в баллах, выставленных двумя экспертами за выполнение любого из заданий 13–19, составляет 2 или более балла. В этом случае третий эксперт проверяет только ответ на то задание, который был оценен двумя экспертами со столь существенным расхождением;
-
расхождения экспертов при оценивании ответов на хотя бы два из заданий 13–19. В этом случае третий эксперт проверяет ответы на все задания работы.
© 2021, Чугаева Олеся Алексеевна 527 0
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
