Единый государственный экзамен по МАТЕМАТИКЕ Тренировочный вариант от 03.03.2025
Профильный уровень Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 12 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.
Часть 1

-
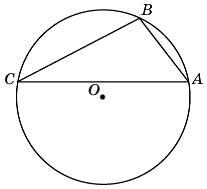 Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
-
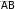
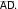 В параллелограмме ABCD известны координаты трёх вершин: А (0; 0), В (5; 0), С (12; 3). Найдите скалярное
В параллелограмме ABCD известны координаты трёх вершин: А (0; 0), В (5; 0), С (12; 3). Найдите скалярное
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки.
При выполнении заданий можно пользоваться черновиком. Записи в
произведение векторов
и
черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.
ЖЕЛАЕМ УСПЕХА!
Справочные материалы
sin 2 cos2 1 sin 2 2 sin cos cos 2 cos2 sin 2
sin sin cos cossin
cos cos cos sin sin
-
Объем параллелепипеда
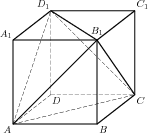
ABCDA1B1C1D1
равен 4,5. Найдите объем треугольной пирамиды
AD1CB1.
-
При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного меньше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 66,99 мм или больше чем 67,01 мм.
-
Вероятность того, что батарейка бракованная, равна 0,09. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
-
Решите уравнение 63x 0, 6 103x.
-

2
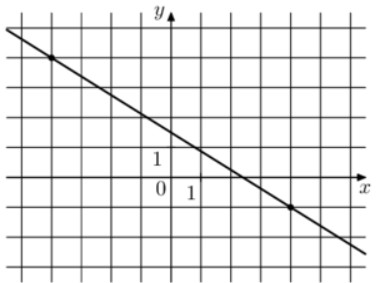
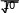 Найдите tg , если cos 1 и a 3π ; 2π .
Найдите tg , если cos 1 и a 3π ; 2π .
-
 На рисунке изображён график функции y F x - одной из
На рисунке изображён график функции y F x - одной из
первообразных некоторой функции
-
Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон — 42000 рублей, Гоша — 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.
-
 На рисунке изображён график функции f x k x b.
На рисунке изображён график функции f x k x b.
f x , определённой на интервале
3; 5 . Пользуясь рисунком,
определите количество решений
Найдите значение x при котором
f x 7, 25.
уравнения
2; 4.
f x 0
на отрезке
-
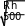
 Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии
Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии
-
Найдите наибольшее значение функции
y 376 x x2 .
горизонта вычисляется по формуле
l , где
R 6400 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
Часть 2
-
Отрезок CH – высота прямоугольного треугольника

Для записи решений и ответов на задания 13-19 используйте БЛАНК ОТВЕТОВ №2. Запишите сначала номер выполняемого задания (13, 14 и т.д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.
ABC с прямым углом
C. На катетах
AC и
BC выбраны точки
M и
 N соответственно такие, что MHN 90 .
N соответственно такие, что MHN 90 .
-
а) Решите уравнение
cos2 2π
x cos
2 2π
x а) Докажите, что треугольник MNH подобен треугольнику
ABC.
б) Найдите CN, если BC = 2, AC = 4, CM = 1.


3
3
б) Найдите все корни этого уравнения, принадлежащие
-
Найдите все значения параметра a, при каждом из
промежутку
5π
 2
2
; π .
которых система уравнений
x2 y 2 4 a 1 x 2ay 5a 2 8a 3 0,
y 2 x2
-
Дана четырёхугольная пирамида SABCD с
 прямоугольником ABCD в основании. Сторона AB равна 3 , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.
прямоугольником ABCD в основании. Сторона AB равна 3 , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.
имеет ровно четыре различных решения.
-
Последовательность a1 , a2 ,..., a7
неотрицательных однозначных чисел. Пусть M k
состоит из
— среднее
а) Докажите, что точка P является серединой отрезка BQ. арифметическое всех членов этой последовательности, кроме k-
б) Найдите угол между плоскостями SBA и SBC, если ребро
SD равно 9.
-
Решите неравенство:
3 3
log
2 x 4
log
2 x 6
0
-
Вклад в размере 6 млн рублей планируется открыть на четыре года. В конце каждого года вклад увеличивается на 10% по сравнению с его размером в начале года, а кроме этого, в начале третьего и четвёртого годов вклад ежегодно пополняется на одну и ту же фиксированную сумму, равную целому числу миллионов рублей. Найдите наименьший возможный размер такой суммы, при которой через четыре года вклад станет не меньше 15 млн рублей. Ответ дайте в млн рублей.
го. Известно, что M 1 1 , M 2 2 .
а) приведите пример такой последовательности, для которой
M 3 1, 5 .
б) существует ли такая последовательность, для которой
M 3 3 ?
в) Найдите наибольшее возможное значение M 3








 Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
Точки A, B, C расположенные на окружности, делят ее на три дуги, градусные меры которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.
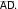 В параллелограмме ABCD известны координаты трёх вершин: А (0; 0), В (5; 0), С (12; 3). Найдите скалярное
В параллелограмме ABCD известны координаты трёх вершин: А (0; 0), В (5; 0), С (12; 3). Найдите скалярное

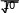 Найдите tg , если cos 1 и a 3π ; 2π .
Найдите tg , если cos 1 и a 3π ; 2π .  На рисунке изображён график функции y F x - одной из
На рисунке изображён график функции y F x - одной из На рисунке изображён график функции f x k x b.
На рисунке изображён график функции f x k x b.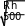
 Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии
Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии

 2
2 прямоугольником ABCD в основании. Сторона AB равна 3 , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.
прямоугольником ABCD в основании. Сторона AB равна 3 , а BC равна 6. Вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника. Из вершин A и C на ребро SB опущены перпендикуляры AP и CQ.


















