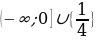Единый государственный экзамен по МАТЕМАТИКЕ Тренировочный вариант от 9.03.2025г
Профильный уровень Инструкция по выполнению работы
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 12 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются по приведённому ниже образцу в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите их в бланк ответов № 1.

При выполнении заданий 13–19 требуется записать полное решение и ответ в бланке ответов № 2.
Все бланки ЕГЭ заполняются яркими чёрными чернилами. Допускается использование гелевой или капиллярной ручки
При выполнении заданий можно пользоваться черновиком. Записи в черновике, а также в тексте контрольных измерительных материалов не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
После завершения работы проверьте, чтобы ответ на каждое задание в бланках ответов № 1 и № 2 был записан под правильным номером.
ЖЕЛАЕМ УСПЕХА!
Справочные материалы
sin 2 cos2 1 sin 2 2 sin cos cos 2 cos2 sin 2
sin sin cos cossin
cos cos cos sin sin
Часть 1
-
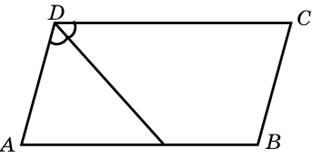 Биссектриса тупого угла параллелограмма ABCD делит противоположную сторону в отношении 4:3, 4:3считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Биссектриса тупого угла параллелограмма ABCD делит противоположную сторону в отношении 4:3, 4:3считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
-
В равнобедренном прямоугольном треугольнике ABC с
 прямым углом C известно, что AB 7
прямым углом C известно, что AB 7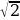 . Найдите скалярное произведение векторов
. Найдите скалярное произведение векторов 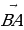 и
и 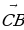
-
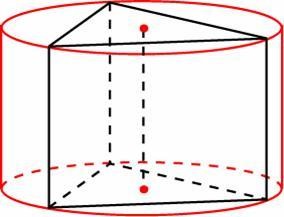
Найдите площадь боковой поверхности
правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен
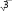 2 , а высота равна 2.
2 , а высота равна 2.
4. В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
5. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в первом автомате закончится кофе, равна 0,35. Вероятность того, что кофе закончится во втором автомате, такая же. Вероятность того, что кофе закончится в двух автоматах, равна 0,16. Найдите вероятность того, что к концу дня кофе останется в двух автоматах.
6. Найдите корень уравнения 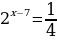
7. 
 Найдите значение выражения 5sin 74
Найдите значение выражения 5sin 74
8.  На рисунке изображен
На рисунке изображен
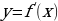 производной функции
производной функции 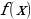
определенной на интервале
9; 2 . Найдите промежутки
убывания функции 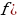 ). В ответе
). В ответе
укажите сумму целых точек, входящих
в эти промежутки.
9. Перед отправкой тепловоз издал гудок с частотой
f0 440 Гц. Чуть позже издал гудок подъезжающий к платформе
тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону
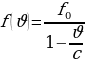 Гц, где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы а c 315 м/с. Ответ выразите в м/с.
Гц, где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы а c 315 м/с. Ответ выразите в м/с.
10. Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
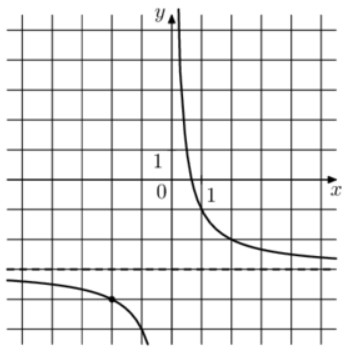
11. На рисунке изображён график
Функции 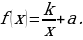 Найдите
Найдите 
12. Найдите наименьшее значение функции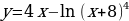 на отрезке
на отрезке 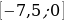
Не забудьте перенести все ответы в бланк ответов № 1 в соответствии с инструкцией по выполнению работы. Проверьте, чтобы каждый ответ был записан в строке с номером соответствующего задания.
Часть 2
Для записи решений и ответов на задания 13-19 используйте БЛАНК ОТВЕТОВ №2. Запишите сначала номер выполняемого задания (13, 14 и т.д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.
13. а) Решите уравнение
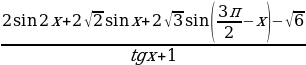
б) Найдите все корни этого уравнения, принадлежащие
промежутку 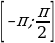 .
.
14. В правильном тетраэдре ABCD с ребром 10 на ребрах AD, BD и AC выбраны точки K, L и M так, что KD 4, MC 6, LD 8. Плоскость, проходящая через точки K, L и M, пересекает ребро BC в точке P.
а) Докажите, что CP : PB 9 :1 .
б) Найдите площадь четырехугольника MKLP
15. Решите неравенство:
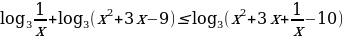
16. 15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы: – 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца; – со 2-го по 14 число каждого месяца необходимо выплатить часть долга; – 15-го числа месяца и все следующие месяцы долг должен быть меньше долга на 15-е число предыдущего месяца на 50 тысяч рублей, в течении 1-го года, на 30 тысяч рублей в течении 2-го года. Найдите сумму выплаченную банку?
17. К окружности, вписанной в квадрат ABCD, проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно.
а) Докажите, что периметр треугольника AMN равен стороне квадрата
б) Прямая MN пересекает прямую CD в точке P. В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
18. Найдите все значения параметра a, при каждом из которых уравнение
|sin 2 x 2 cos x a| sin 2 x cos x a
имеет на промежутке  единственный корень.
единственный корень.
19. Есть четыре коробки: в первой коробке 101 камень, во второй — 102, в третьей — 103, а в четвёртой коробке камней нет. За один ход берут по одному камню из любых трёх коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.
а) Могло ли в первой коробке оказаться 97 камней, во второй — 102, в третье — 103, а в четвёртой — 4?
б) Могло ли в четвёртой коробке оказаться 306 камней?
в) Какое наибольшее число камней могло оказаться в первой коробке?
| 1 | 28 |
|
13 | 3π 2πk; π 2πk; а) 4 3 2π 2πk ; k Z ; 3 б) 3π ; π . 4 3 |
| 2 | – 49 |
| 14 | 11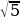 . . |
| 3 | 36 |
| 15 | 2; . |
| 4 | 0,48 |
| 16 | 1 065 600. |
| 5 | 0,46 |
| 17 | 1 : 3. |
| 6 | 5 |
|
18 | 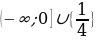
|
| 7 | 10 |
|
19 | а) да; б) нет; в) 303. |
| 8 | – 22 |
|
|
|
| 9 | 7 |
|
|
|
| 10 | 90 |
|
|
|
| 11 | – 2,96 |
|
|
|
| 12 | – 28 |
|
|
|







 Биссектриса тупого угла параллелограмма ABCD делит противоположную сторону в отношении 4:3, 4:3считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.
Биссектриса тупого угла параллелограмма ABCD делит противоположную сторону в отношении 4:3, 4:3считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88. прямым углом C известно, что AB 7
прямым углом C известно, что AB 7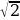 . Найдите скалярное произведение векторов
. Найдите скалярное произведение векторов 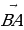 и
и 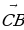
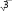 2 , а высота равна 2.
2 , а высота равна 2.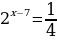
 Найдите значение выражения 5sin 74
Найдите значение выражения 5sin 74 На рисунке изображен
На рисунке изображен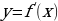 производной функции
производной функции 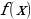
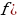 ). В ответе
). В ответе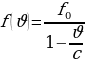 Гц, где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы а c 315 м/с. Ответ выразите в м/с.
Гц, где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы а c 315 м/с. Ответ выразите в м/с.
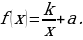 Найдите
Найдите 
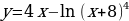 на отрезке
на отрезке 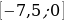
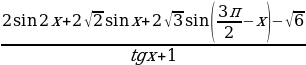
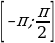 .
. 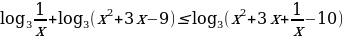
 единственный корень.
единственный корень.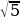 .
.