Третий признак равенства треугольников

Третий признак равенства треугольников

Цели:

• Познакомить учащихся со свойством жесткости треугольника Изучить третий признак равенства треугольников.
• Изучить третий признак равенства треугольников.
• Формировать умения, навыки решения задач на признаки равенства треугольников.
• Систематизировать, расширить и углубить знания учащихся о треугольнике.

Задачи:

• 1.Сформулировать и доказать третий признак равенства треугольников.
• 2. Использовать знания 1-го признака равенства треугольников для доказательства теоремы.
• 3. Систематизировать знания и умения учащихся решать задачи, используя признаки равенства треугольников.
• 4. Развивать основы логического и алгоритмического мышления, расширять кругозор учащихся, учить произвольно и осознанно владеть приемами решения задач.

Как вы думаете, что такое жесткая фигура?

Жесткая фигура — это фигура, не подверженная деформации

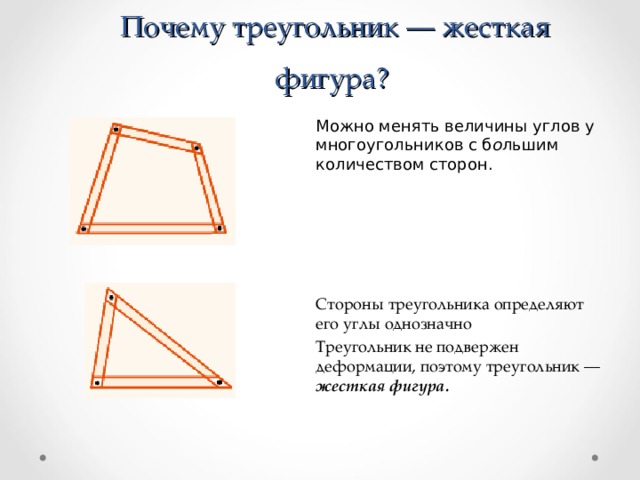
  Почему треугольник — жесткая фигура?

Можно менять величины углов у многоугольников с б о льшим количеством сторон.

Стороны треугольника определяют его углы однозначно

Треугольник не подвержен деформации, поэтому треугольник — жесткая фигура.

Третий признак равенства треугольников

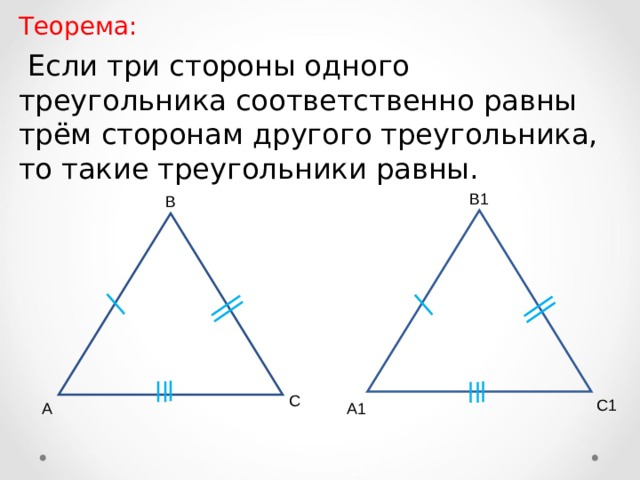
Теорема:

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

В1

В

С

С1

А

А1

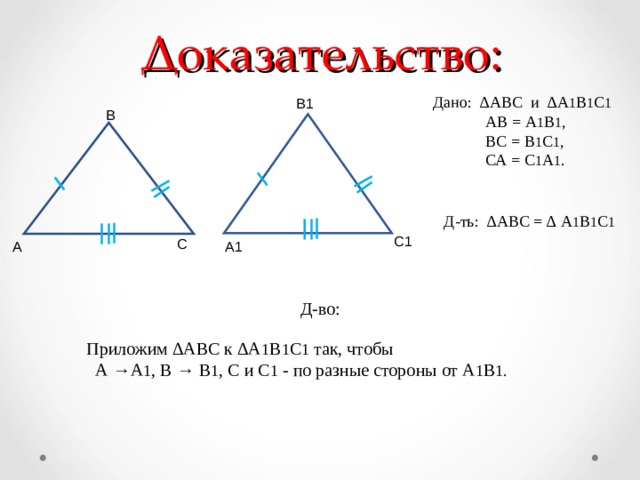
Доказательство:

Дано: ∆АВС и ∆А 1 В 1 С 1

АВ = А 1 В 1 ,

ВС = В 1 С 1 ,

СА = С 1 А 1 .

В1

В

Д-ть: ∆АВС = ∆ А 1 В 1 С 1

С1

С

А1

А

Д-во:

Приложим ∆АВС к ∆А 1 В 1 С 1 так, чтобы

А →А 1 , В → В 1 , С и С 1 - по разные стороны от А 1 В 1.

А 1 (А)

2

1

С

С 1

4

3

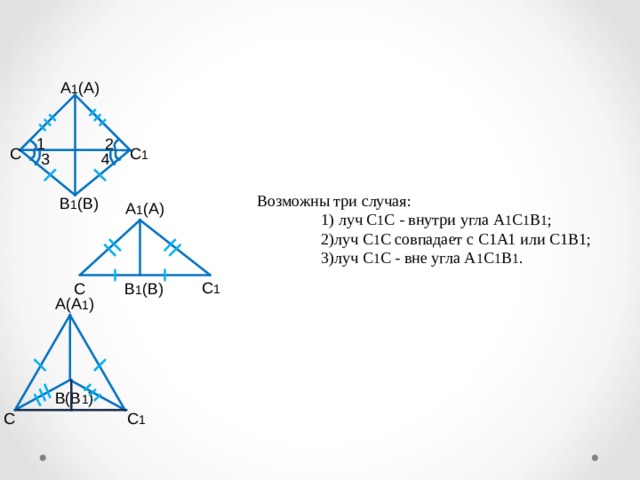
Возможны три случая:

1) луч С 1 С - внутри угла А 1 С 1 В 1 ;

2)луч С 1 С совпадает с С1А1 или С1В1;

3)луч С 1 С - вне угла А 1 С 1 В 1 .

В 1 (В)

А 1 (А)

С 1

В 1 (В)

С

А(А 1 )

В(В 1 )

С 1

С

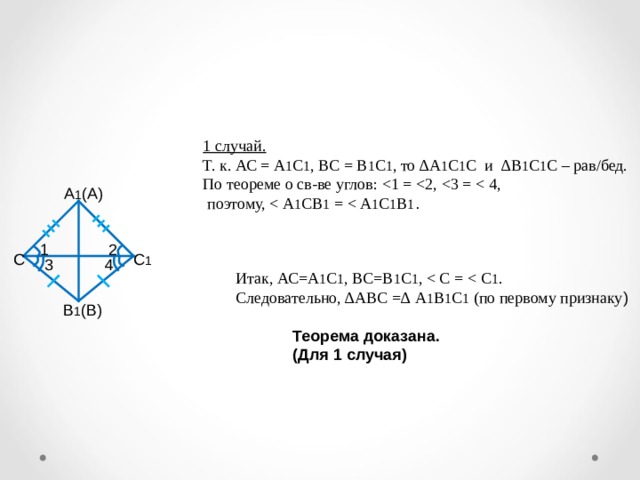
1 случай.

Т. к. АС = А 1 С 1 , ВС = В 1 С 1 , то ∆А 1 С 1 С и ∆В 1 С 1 С – рав/бед. По теореме о св-ве углов:

поэтому,

А 1 (А)

1

2

С 1

С

3

4

Итак, АС=А 1 С 1 , ВС=В 1 С 1 ,

Следовательно, ∆АВС =∆ А 1 В 1 С 1 (по первому признаку )

В 1 (В)

Теорема доказана.

(Для 1 случая)

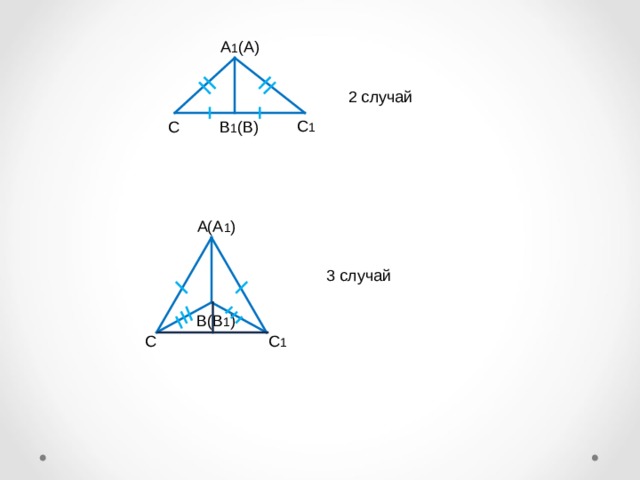
А 1 (А)

2 случай

С 1

С

В 1 (В)

А(А 1 )

3 случай

В(В 1 )

С 1

С

∆АВС= ∆ CDA (по 3 признаку) Ч.и т.д. " width="640"

Решим задачу:

Дано:

ABCD

АС-диагональ

АВ= CD

ВС= AD

Док - ть:

∆ АВС= ∆ CDA

B

C

D

А

Решение: 1) АС-общая для ∆АВС и ∆ CDA

2) АВ= CD по условию

3) ВС= AD по условию

= ∆АВС= ∆ CDA (по 3 признаку)

Ч.и т.д.

Спасибо за внимание

Литература:

• Геометрия 7-9кл. Атанасян Л.С. И др.