СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 07.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Обо мне Блог Файлы Тесты Галерея Активность Награды

Тренировочный вариант№4, профильный

Категория: Математика

Нажмите, чтобы узнать подробности

Тренировочный вариант ЕГЭ по математике №9, профильный

Просмотр содержимого документа
«Тренировочный вариант№4, профильный»

Вариант № 1

1. Шо­ко­лад­ка стоит 40 руб­лей. В вос­кре­се­нье в су­пер­мар­ке­те дей­ству­ет спе­ци­аль­ное пред­ло­же­ние: за­пла­тив за три шо­ко­лад­ки, по­ку­па­тель по­лу­ча­ет че­ты­ре (одну в по­да­рок). Какое наи­боль­шее ко­ли­че­ство шо­ко­ла­док можно по­лу­чить, по­тра­тив не более 200 руб­лей в вос­кре­се­нье?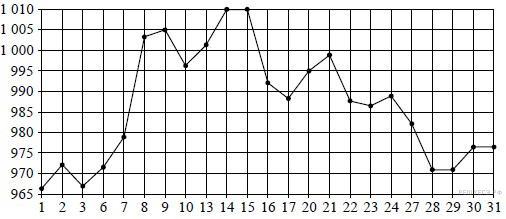

2. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­на цена зо­ло­та, уста­нов­лен­ная Цен­тро­бан­ком РФ, во все ра­бо­чие дни в ок­тяб­ре 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена зо­ло­та в руб­лях за грамм. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку наи­боль­шую цену зо­ло­та на мо­мент за­кры­тия тор­гов в пе­ри­од с 3 по 13 ок­тяб­ря (в руб­лях за грамм).

3. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 1 изоб­ражён угол. Най­ди­те тан­генс этого угла.

4. В сбор­ни­ке би­ле­тов по фи­ло­со­фии всего 25 би­ле­тов, в 8 из них встре­ча­ет­ся во­прос по теме "Пи­фа­гор". Най­ди­те ве­ро­ят­ность того, что в слу­чай­но вы­бран­ном на эк­за­ме­не би­ле­те школь­ни­ку не до­ста­нет­ся во­про­са по теме "Пи­фа­гор".

5. Ре­ши­те урав­не­ние .

6. 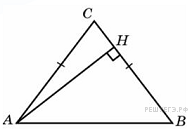В тре­уголь­ни­ке ABC AC = BC, AB = 6, 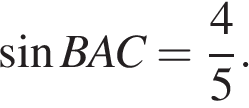Най­ди­те вы­со­ту AH.

7. На ри­сун­ке изоб­ра­жен гра­фик функ­ции 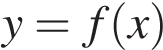и от­ме­че­ны точки −2, −1, 3, 4. В какой из этих точек зна­че­ние про­из­вод­ной наи­боль­шее? В от­ве­те ука­жи­те эту точку.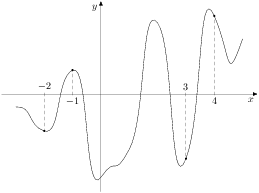

8. 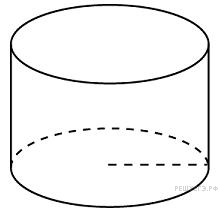Ра­ди­ус ос­но­ва­ния ци­лин­дра равен 2, вы­со­та равна 3. Най­ди­те пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра, де­лен­ную на .

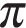9. Най­ди­те если и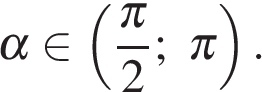

10. Рас­сто­я­ние от на­блю­да­те­ля, на­хо­дя­ще­го­ся на не­боль­шой вы­со­те 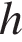ки­ло­мет­ров над землёй, до на­блю­да­е­мой им линии го­ри­зон­та вы­чис­ля­ет­ся по фор­му­л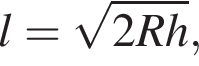е где 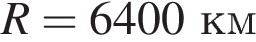— ра­ди­ус Земли. С какой вы­со­ты го­ри­зонт виден на рас­сто­я­нии 160 ки­ло­мет­ров? Ответ вы­ра­зи­те в ки­ло­мет­рах.

11. В по­не­дель­ник акции ком­па­нии по­до­ро­жа­ли на не­ко­то­рое ко­ли­че­ство про­цен­тов, а во втор­ник по­де­ше­ве­ли на то же самое ко­ли­че­ство про­цен­тов. В ре­зуль­та­те они стали сто­ить на 1% де­шев­ле, чем при от­кры­тии тор­гов в по­не­дель­ник. На сколь­ко про­цен­тов по­до­ро­жа­ли акции ком­па­нии в по­не­дель­ник?

12. Най­ди­те наи­мень­шее зна­че­ние функ­ции 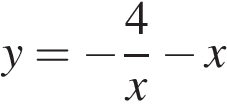на от­рез­ке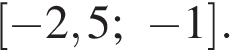

13. а) Ре­ши­те урав­не­ние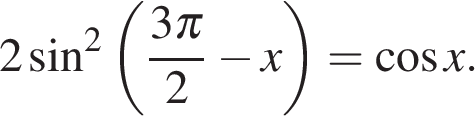

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку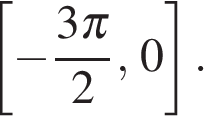 

14. Плос­кость α пе­ре­се­ка­ет два шара, име­ю­щих общий центр. Пло­щадь се­че­ния мень­ше­го шара этой плос­ко­стью равна 6. Плос­кость β, па­рал­лель­ная плос­ко­сти α, ка­са­ет­ся мень­ше­го шара, а пло­щадь се­че­ния этой плос­ко­стью боль­ше­го шара равна 4. Най­ди­те пло­щадь се­че­ния боль­ше­го шара плос­ко­стью α.

15. Ре­ши­те не­ра­вен­ство: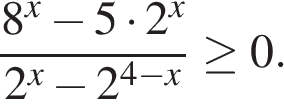


16. Бо­ко­вые сто­ро­ны AB и CD тра­пе­ции ABCD равны 6 и 8 со­от­вет­ствен­но. От­ре­зок, со­еди­ня­ю­щий се­ре­ди­ны диа­го­на­лей, равен 5, сред­няя линия тра­пе­ции равна 25. Пря­мые AB и CD пе­ре­се­ка­ют­ся в точке М. Най­ди­те ра­ди­ус окруж­но­сти, впи­сан­ной в тре­уголь­ник ВМС.

17. В июле 2016 года пла­ни­ру­ет­ся взять кре­дит в банке на три года в раз­ме­ре S млн руб­лей, где S — целое число. Усло­вия его воз­вра­та та­ко­вы:

− каж­дый ян­варь долг уве­ли­чи­ва­ет­ся на 25% по срав­не­нию с кон­цом преды­ду­ще­го года;

− с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить одним пла­те­жом часть долга;

− в июле каж­до­го года долг дол­жен со­став­лять часть кре­ди­та в со­от­вет­ствии со сле­ду­ю­щей таб­ли­цей

 

Месяц и год

Июль 2016

Июль 2017

Июль 2018

Июль 2019

Долг

(в млн руб­лей)

S

0,7S

0,4S

0

 

Най­ди­те наи­мень­шее S, при ко­то­ром каж­дая из вы­плат будет боль­ше 5 млн руб­лей.


18. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых функ­ция 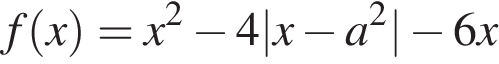имеет более двух точек экс­тре­му­ма.


19. Семь экс­пер­тов оце­ни­ва­ют ки­но­фильм. Каж­дый из них вы­став­ля­ет оцен­ку — целое число бал­лов от 0 до 10 вклю­чи­тель­но. Из­вест­но, что все экс­пер­ты вы­ста­ви­ли раз­лич­ные оцен­ки. По ста­рой си­сте­ме оце­ни­ва­ния рей­тинг ки­но­филь­ма — это сред­нее ариф­ме­ти­че­ское всех оце­нок экс­пер­тов. По новой си­сте­ме оце­ни­ва­ния рей­тинг ки­но­филь­ма оце­ни­ва­ют сле­ду­ю­щим об­ра­зом: от­бра­сы­ва­ют­ся наи­мень­шая и наи­боль­шая оцен­ки и под­счи­ты­ва­ет­ся сред­нее ариф­ме­ти­че­ское остав­ших­ся оце­нок.

а) Может ли раз­ность рей­тин­гов, вы­чис­лен­ных по ста­рой и новой си­сте­мам оце­ни­ва­ния рав­нять­ся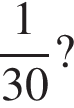

б) Может ли раз­ность рей­тин­гов, вы­чис­лен­ных по ста­рой и новой си­сте­мам оце­ни­ва­ния рав­нять­ся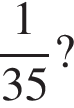

в) Най­ди­те наи­боль­шее воз­мож­ное зна­че­ние раз­но­сти рей­тин­гов, вы­чис­лен­ных по ста­рой и новой си­с­те­мам оце­ни­ва­ния.

Электронная тетрадь по геометрии 9...

Математика 6 класс ФГОС

Электронная тетрадь по алгебре 8 класс...

Математика 6 класс

Алгебра 10 класс

Электронная тетрадь по алгебре 11 класс...

Алгебра 10 класс ФГОС

Геометрия 10 класс ФГОС
Скачать

© 2017, 1285 14

Рекомендуем курсы ПК и ППК для учителей

Методика подготовки к ОГЭ по математике
800 руб.  4000 руб.
Использование табличного процессора в обучении математике
600 руб.  3000 руб.
Методика преподавания математики в соответствии с ФГОС ООО (СОО)
800 руб.  4000 руб.
Интерактивные методы в практике школьного образования
800 руб.  4000 руб.
Исследовательская деятельность учащихся
800 руб.  4000 руб.
Методы решения функциональных уравнений и неравенств
800 руб.  4000 руб.

Похожие файлы

1 комментарий
09.04.2017 19:12
Иванова Любовь Ивановна @lybas
спасибо.

Вебинар для учителей

Свидетельство об участии БЕСПЛАТНО!

Полезное для учителя

Новости проекта
03.06.24

Лайфхак учителя №1! Что делать с плохой накопляемостью отметок

12.05.24

Лайфхак учителя №2! Как перестать бегать от ученика к ученику во время практической работы

04.05.24

Лайфхак учителя №3! Что делать, если вы устали из урока в урок повторять одно и то же

Курсы для учителей!
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Современные педагогические технологии в образовательном процессе
800 руб.
4000 руб.
Проектная деятельность учащихся
800 руб.
4000 руб.
Учитель, преподаватель математики
2760 руб.
13800 руб.
Смотреть все курсы


Поделитесь с друзьями
ВКонтактеОдноклассникиTwitterМой МирLiveJournalGoogle PlusЯндекс