Третий признак равенства треугольников

Третий признак равенства треугольников.

Теорема:

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

С

С 1

Дано:∆АВС,∆А 1 В 1 С 1, АВ=А 1 В 1 ,ВС=В 1 С 1 ,

СА=С 1 А 1.

Доказать:∆АВС=∆А 1 В 1 С 1.

В

А

А 1

В 1

Доказательство.Приложим ∆АВС к ∆А 1 В 1 С 1 так, чтобы вершина А совместилась с вершиной А 1 ,В- с В 1 ,С иС 1 оказались по разные стороны от прямой А 1 В 1 . Возможны три случая:

С 1

С 1

С 1

в)

б)

а)

А 1

В 1

А 1

В 1

В 1

А 1

С

С

С

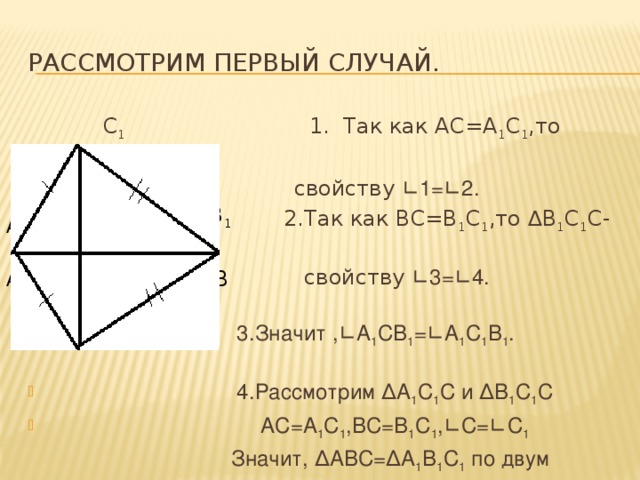
Рассмотрим первый случай.

С 1 1. Так как АС=А 1 С 1 ,то ∆А 1 С 1 С- р/б, по

свойству ∟1=∟2.

• 2.Так как ВС=В 1 С 1 ,то ∆В 1 С 1 С-р/б, по
• свойству ∟3=∟4.
• 3.Значит ,∟А 1 СВ 1 =∟А 1 С 1 В 1 .
• 4.Рассмотрим ∆А 1 С 1 С и ∆В 1 С 1 С
• АС=А 1 С 1 ,ВС=В 1 С 1 ,∟С=∟С 1

Значит, ∆АВС=∆А 1 В 1 С 1 по двум

С сторонам и углу между ними.

4

2

4

2

В 1

В 1

А 1

А

В

В

1

3

1

3

Задача 1 .(решена)

D

Дано: MP=PD,

MQ=QD.

Доказать: ∟D=∟M.

Доказательство.

Рассмотрим ∆MPQ и ∆РDQ

1.MP=PD по условию,

2.MQ=QD по условию,

3.PQ общая.

4.Значит, ∆MPQ=∆PDQ по трём сторонам.

5.В равных треугольниках соответственные элементы равны, следовательно ∟D=∟M.

Q

P

M

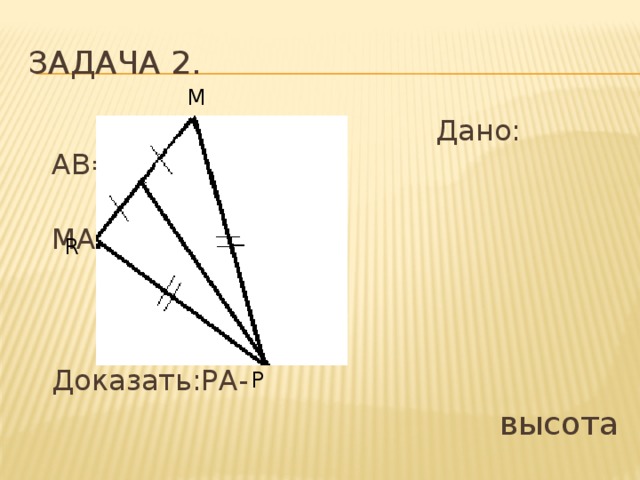
Задача 2.

М

Дано: АВ=DC,

MA=AR

Доказать:РА-

высота

А

R

Р

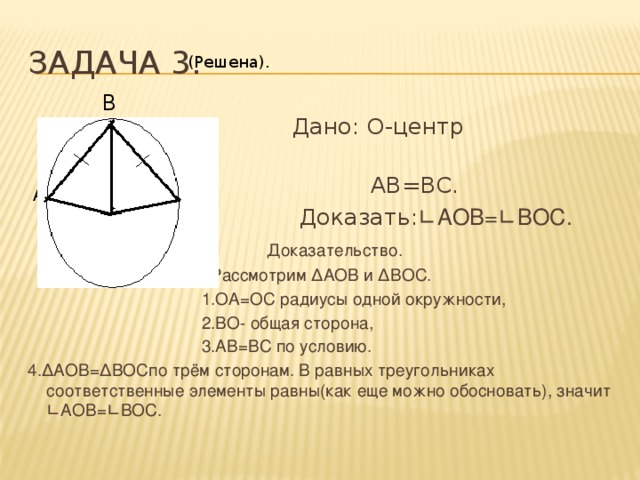
Задача 3.

(Решена).

В

Дано: О-центр окружности,

АВ=ВС.

Доказать: ∟АОВ=∟ВОС.

Доказательство.

Рассмотрим ∆АОВ и ∆ВОС.

1.ОА=ОС радиусы одной окружности,

2.ВО- общая сторона,

3.АВ=ВС по условию.

4.∆АОВ=∆ВОСпо трём сторонам. В равных треугольниках соответственные элементы равны(как еще можно обосновать), значит ∟АОВ=∟ВОС.

А

С

О

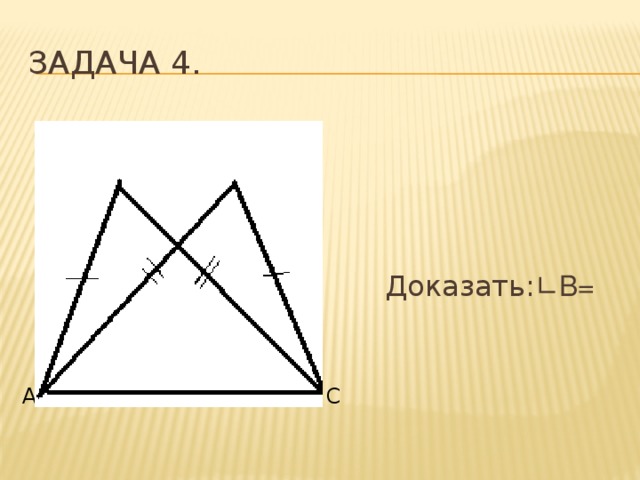
Задача 4.

Дано:АВ=В 1 С,

ВС=АВ 1 .

Доказать: ∟В= ∟В1 ∟В 1 .

В

В1

А

С

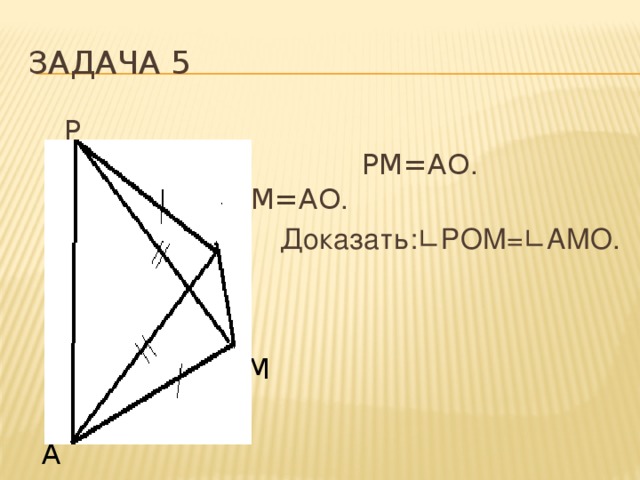
Задача 5

Р Дано:РО=АМ, РМ=АО . РМ=АО .

Доказать:∟РОМ=∟АМО.

О

М

А

Задача 6.

На рисунке АВ=ВС,AD=DC.

Докажите, что ВD-биссектриса угла АВС.

В

D

С

А

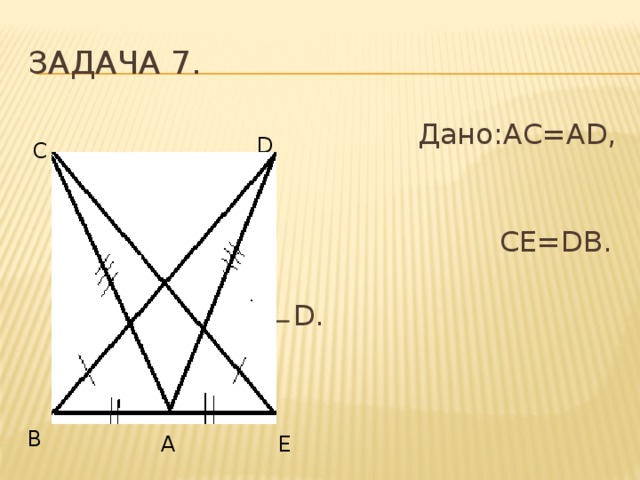
Задача 7.

Дано:AC=AD, AD=BC, AD=BC,

CE=DB.

Доказать: ∟ С= ∟ D.

D

С

В

А

Е

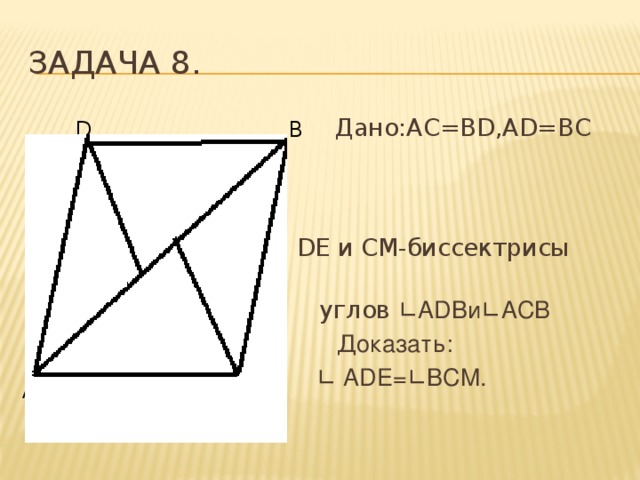
Задача 8.

Дано:AC=BD,AD=BC

DE и СМ-биссектрисы

углов ∟ADBи∟АСВ

Доказать:

∟ ADE=∟BCM.

D

B

M

E

A

C

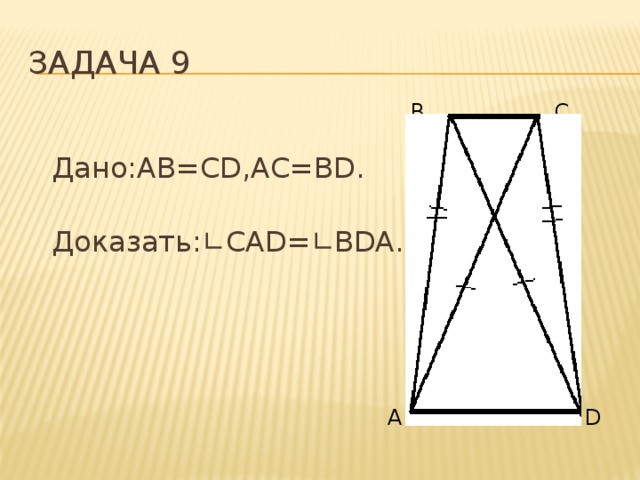
Задача 9

B

C

Дано:AB=CD,AC=BD.

Доказать: ∟ CAD= ∟ BDA.

A

D

Сласибо

за

работу.

Материал подобрала

Канашевская М.С.,

учитель школы №76,г.Лесгной.