
Тригонометрические функции
Воловик Оксана Викторовна,
преподаватель математики ГПОУ «Донецкий транспортно-экономический колледж»
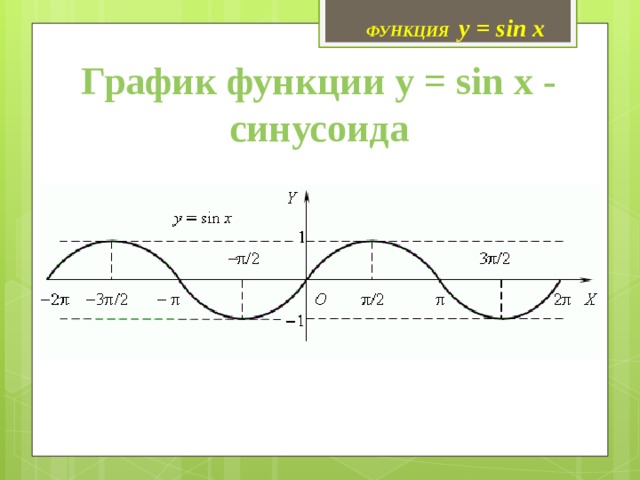
ФУНКЦИЯ y = sin x
График функции y = sin x - синусоида
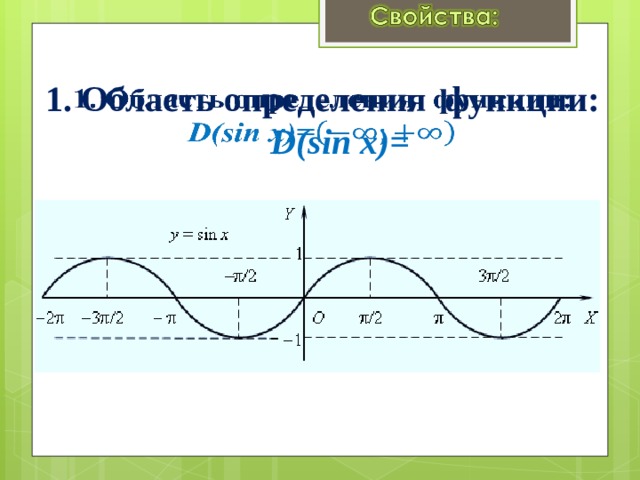
1. Область определения функции: D(sin x)=
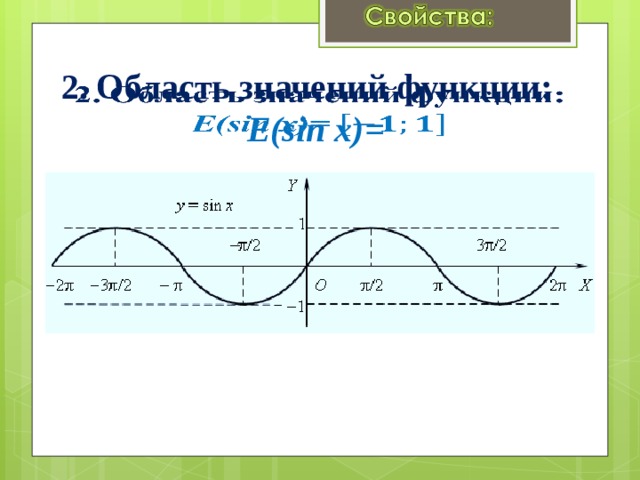
2. Область значений функции: E(sin x)=
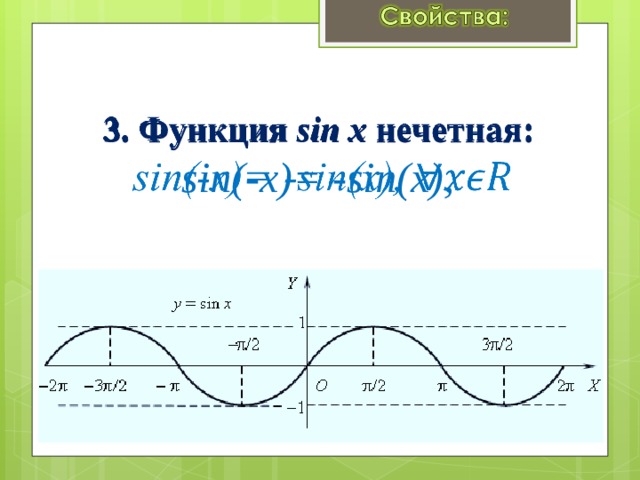
3. Функция sin x нечетная: sin(-x)= -sin(x),
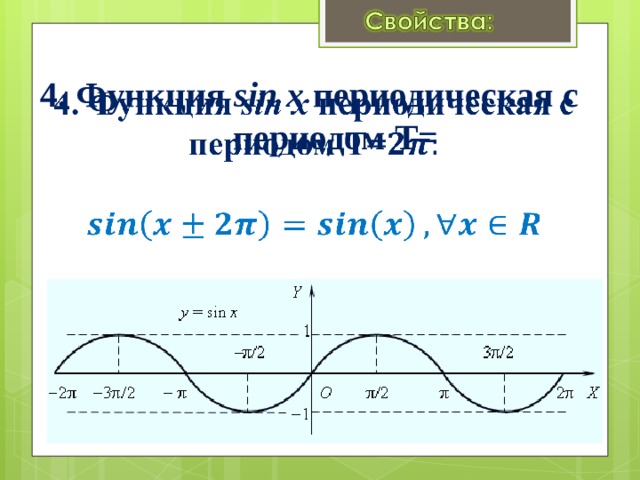
4. Функция sin x периодическая с периодом Т=
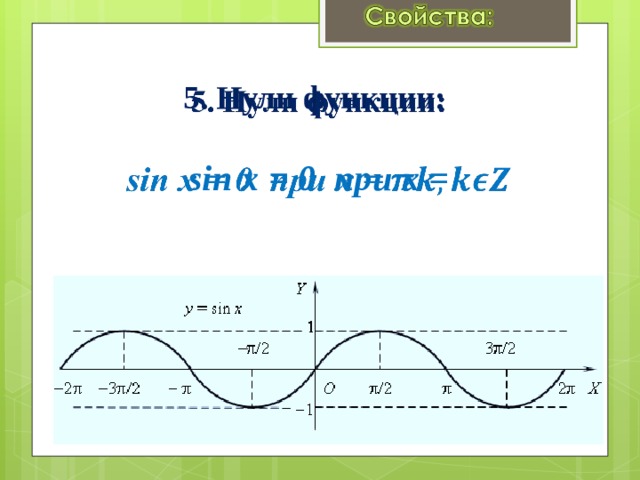
5. Нули функции: sin x = 0 при x =
 0 при x2), k Z, sin х Z " width="640"
0 при x2), k Z, sin х Z " width="640"
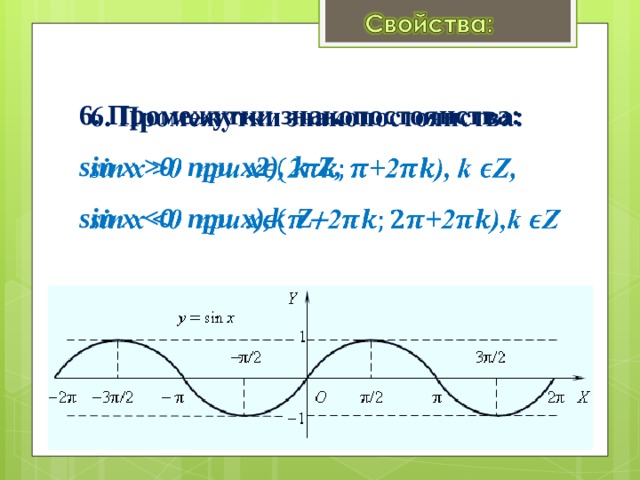
6. Промежутки знакопостоянства: sin х 0 при x2), k Z, sin х Z
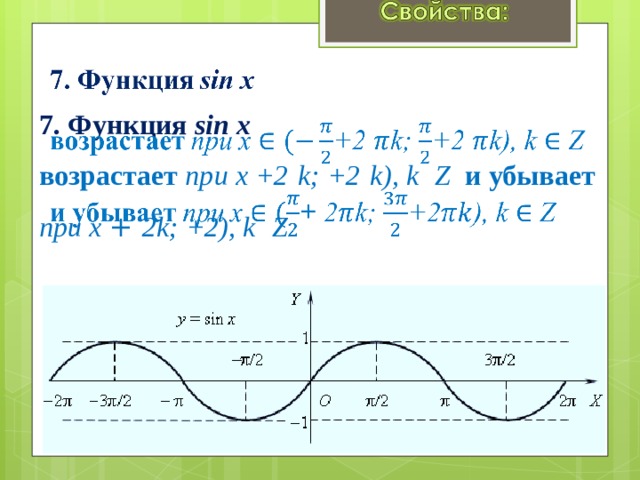
7. Функция sin x возрастает при x +2 k; +2 k), k Z и убывает при x + 2k; +2), k Z
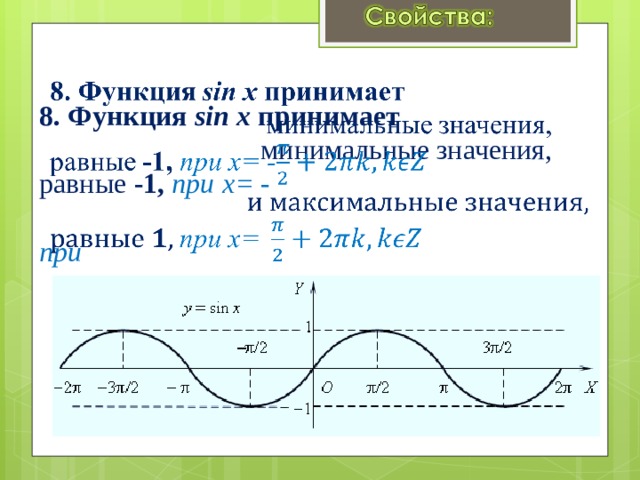
8. Функция sin x принимает минимальные значения, равные -1, при x= - при
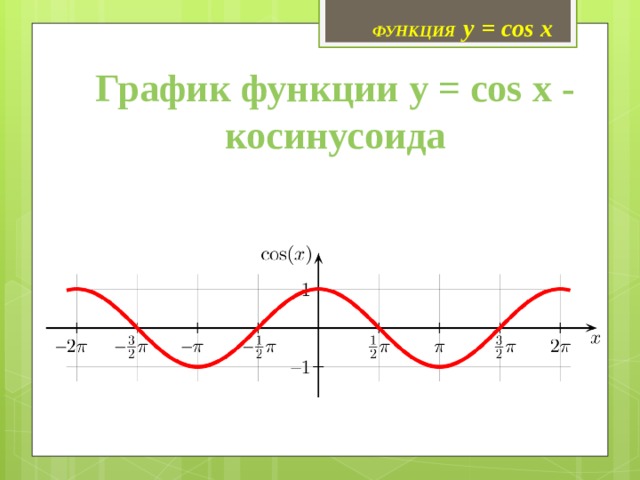
ФУНКЦИЯ y = cos x
График функции y = cos x - косинусоида

1. Область определения функции: D(cos x)=
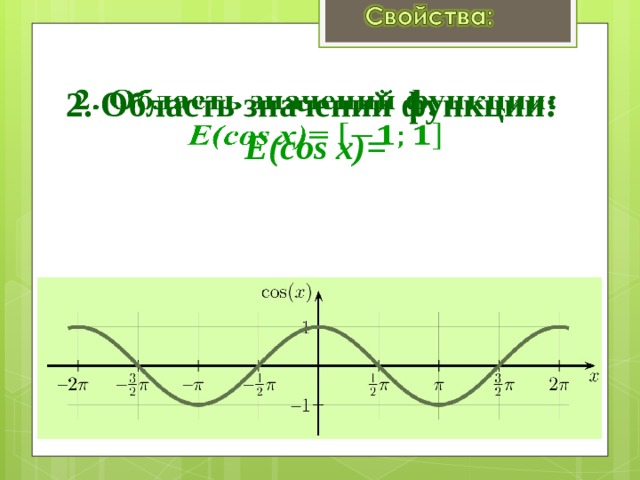
2. Область значений функции: E(cos x)=
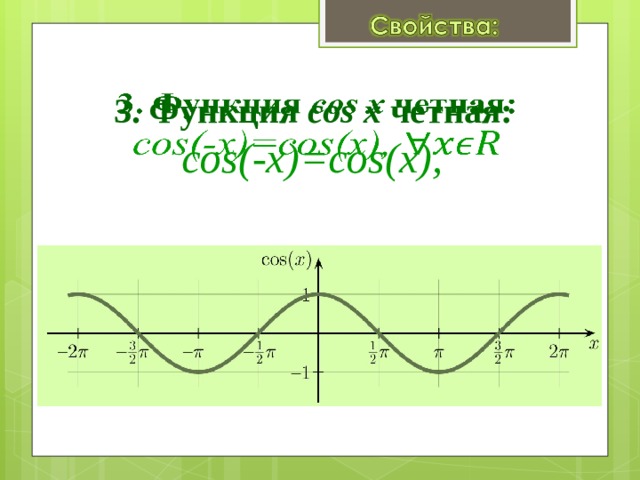
3. Функция cos x четная: cos(-x)=cos(x),
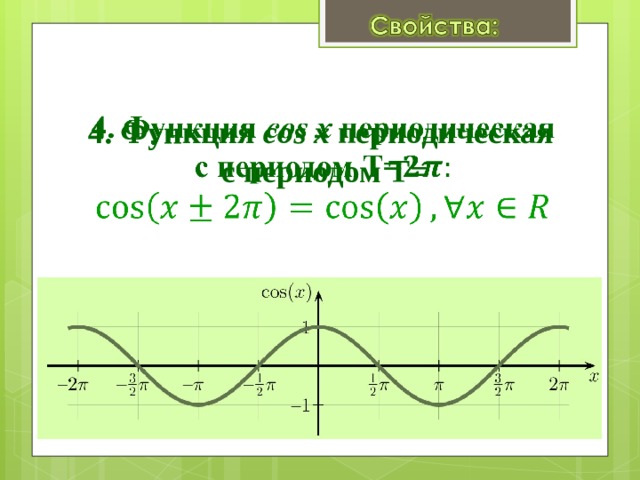
4. Функция cos x периодическая с периодом Т=
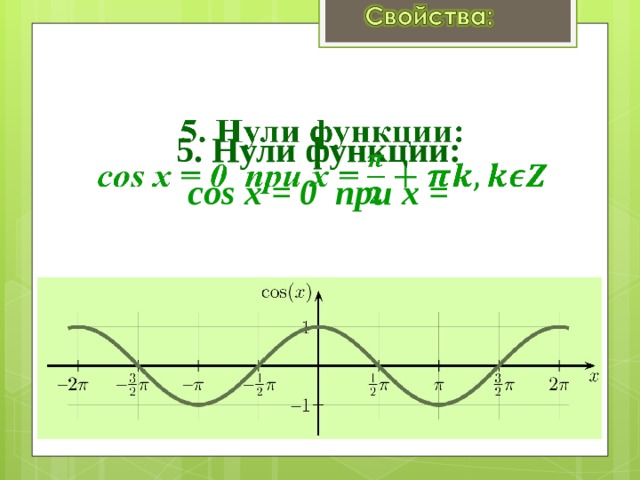
5. Нули функции: cos x = 0 при x =
 0 при x +2), k Z, cos х Z " width="640"
0 при x +2), k Z, cos х Z " width="640"
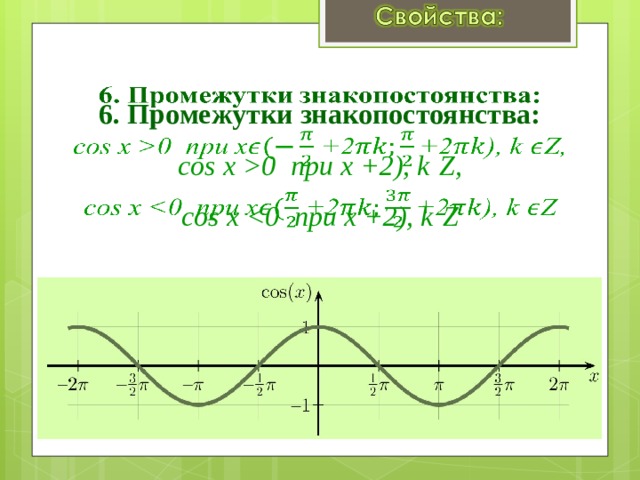
6. Промежутки знакопостоянства: cos х 0 при x +2), k Z, cos х Z
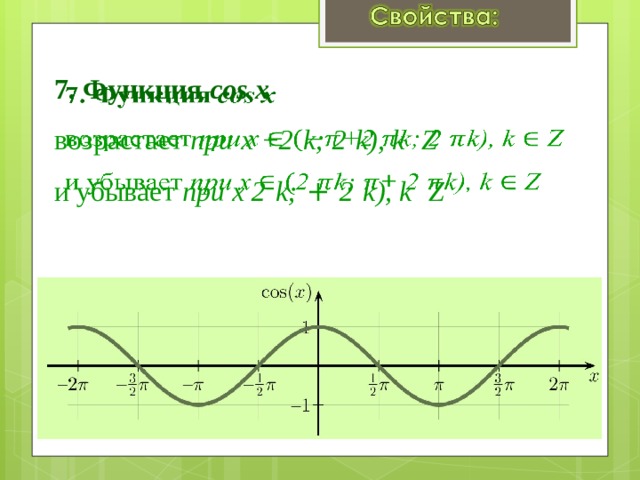
7. Функция cos x возрастает при x +2 k; 2 k), k Z и убывает при x 2 k; + 2 k), k Z
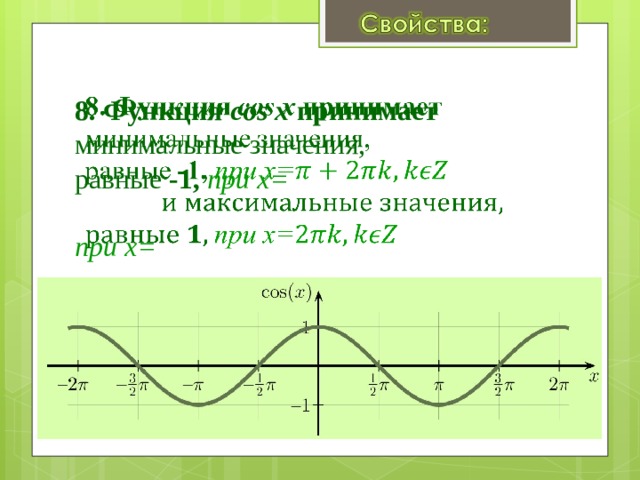
8. Функция cos x принимает минимальные значения, равные -1, при х= при x=

ФУНКЦИЯ y = tg x
График функции y = tg x - тангенсоида

Свойства:
1. Область определения функции: D(tg x) =

2. Область значений функции: E(tg x)=

3. Функция нечетная: tg(-x)= - tg x

4. Функция периодическая с периодом Т=

5. Нули функции: tg x = 0 при x = πk, k ϵ Z
 0 при x + ), k Z tg x " width="640"
0 при x + ), k Z tg x " width="640"
6. Промежутки знакопостоянства: tg x0 при x + ), k Z tg x

7. Функция tg x возрастает на каждом из промежутков своей области определения , т.е. на каждом из промежутков + + ), k
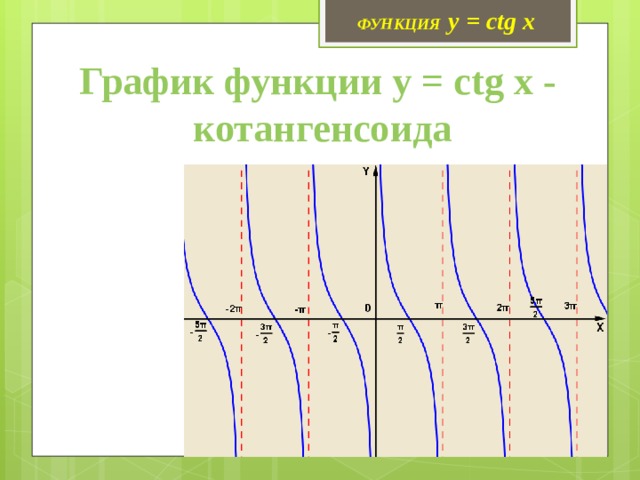
ФУНКЦИЯ y = ctg x
График функции y = сtg x - котангенсоида
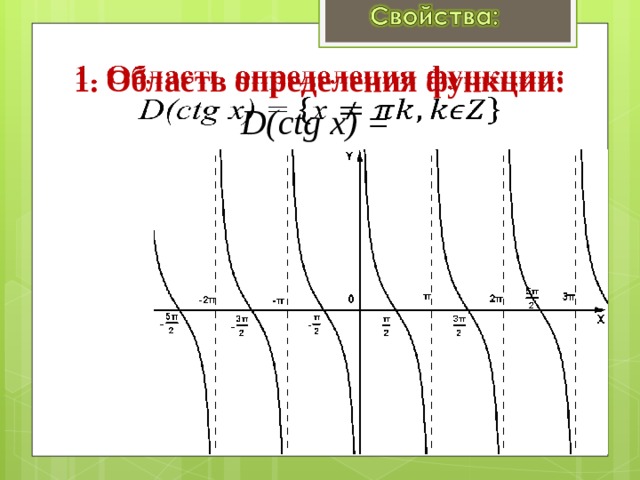
1. Область определения функции: D(сtg x) =
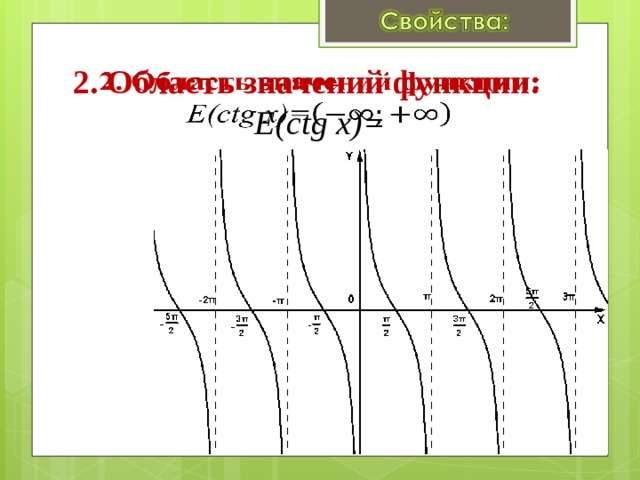
2. Область значений функции: E(ctg x)=
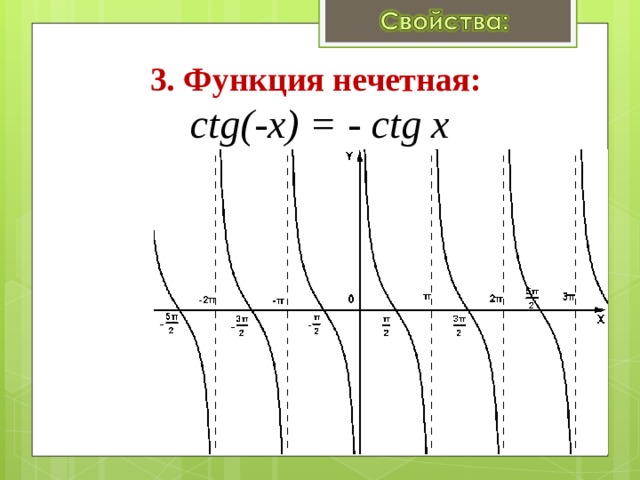
3. Функция нечетная: сtg(-x) = - сtg x
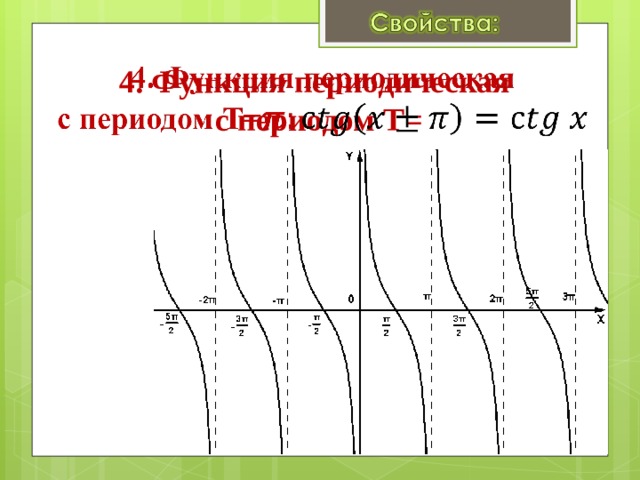
4. Функция периодическая с периодом Т=
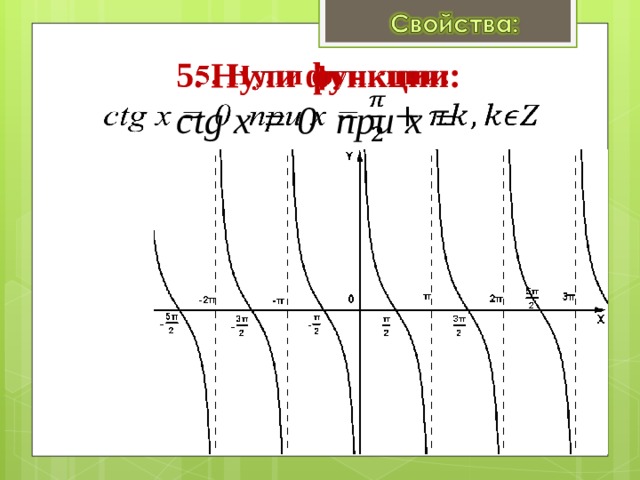
5. Нули функции: ctg x = 0 при x =
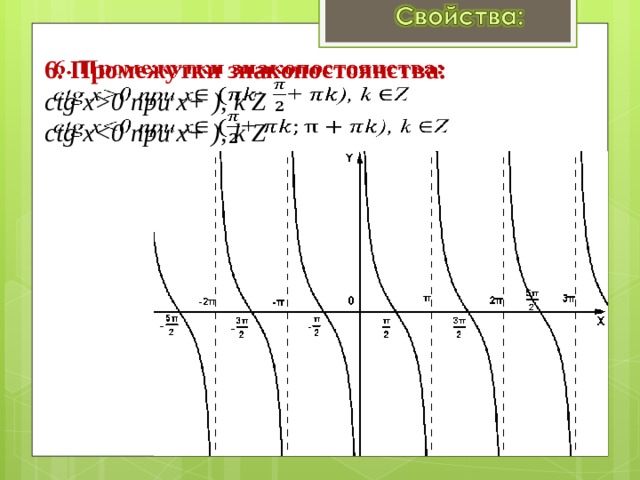 0 при x+ ), k Z сtg x " width="640"
0 при x+ ), k Z сtg x " width="640"
6. Промежутки знакопостоянства: сtg x0 при x+ ), k Z сtg x
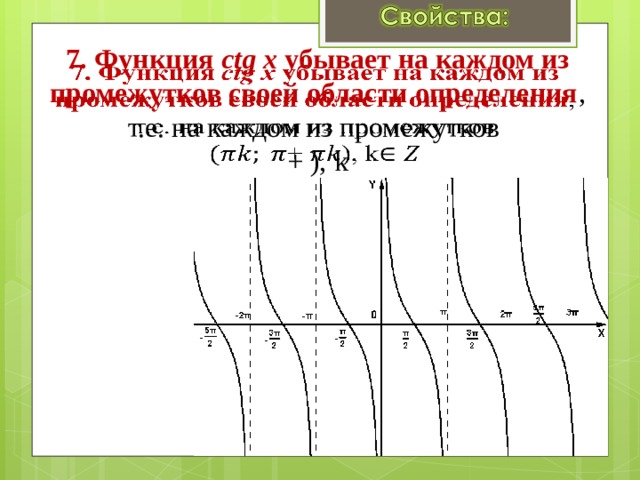
7. Функция сtg x убывает на каждом из промежутков своей области определения , т.е. на каждом из промежутков + ), k

КОНЕЦ!













 0 при x2), k Z, sin х Z " width="640"
0 при x2), k Z, sin х Z " width="640"








 0 при x +2), k Z, cos х Z " width="640"
0 при x +2), k Z, cos х Z " width="640"








 0 при x + ), k Z tg x " width="640"
0 при x + ), k Z tg x " width="640"







 0 при x+ ), k Z сtg x " width="640"
0 при x+ ), k Z сtg x " width="640"





















