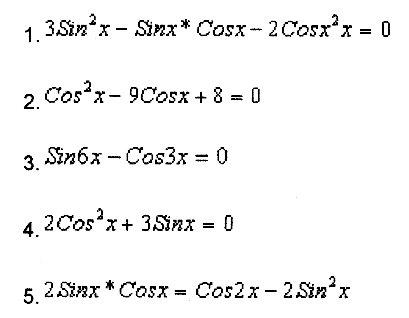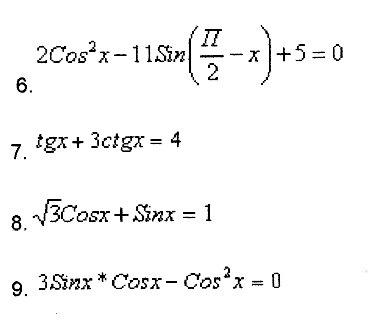"Тригонометрические уравнения"

ТЕМА: «РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ».

ПРЕПОДАВАТЕЛЬ МАТЕМАТИКИ

ГБПОУ МЕСЯГУТОВСКИЙ

ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ

МАТЮШИНА Л.И.

«УЧИТЬСЯ МОЖНО ТОЛЬКО ВЕСЕЛО… ЧТОБЫ ПЕРЕВАРИВАТЬ ЗНАНИЯ, НАДО ПОГЛОЩАТЬ ИХ С АППЕТИТОМ»

АНАТОЛЬ ФРАНС

ЦЕЛИ УРОКА:

• ОБРАЗОВАТЕЛЬНЫЕ – ОБЕСПЕЧИТЬ ПОВТОРЕНИЕ, ОБОБЩЕНИЕ И СИСТЕМАТИЗАЦИЮ МАТЕРИАЛА ТЕМЫ; СОЗДАТЬ УСЛОВИЯ КОНТРОЛЯ УСВОЕНИЯ ЗНАНИЙ И УМЕНИЙ;

• РАЗВИВАЮЩИЕ – СПОСОБСТВОВАТЬ ФОРМИРОВАНИЮ УМЕНИЙ ПРИМЕНЯТЬ ПРИЁМЫ: СРАВНЕНИЯ, ОБОБЩЕНИЯ, ВЫДЕЛЕНИЯ ГЛАВНОГО, ПЕРЕНОСА ЗНАНИЙ В НОВУЮ СИТУАЦИЮ, РАЗВИТИЮ МАТЕМАТИЧЕСКОГО КРУГОЗОРА, МЫШЛЕНИЯ И РЕЧИ, ВНИМАНИЯ И ПАМЯТИ;

• ВОСПИТАТЕЛЬНЫЕ – СОДЕЙСТВОВАТЬ ВОСПИТАНИЮ ИНТЕРЕСА К МАТЕМАТИКЕ И ЕЁ ПРИЛОЖЕНИЯМ, АКТИВНОСТЬ, МОБИЛЬНОСТЬ, УМЕНИЯ ОБЩАТЬСЯ, ОБЩЕЙ КУЛЬТУРЫ.

ТИП УРОКА:

УРОК ОБОБЩЕНИЯ И СИСТЕМАТИЗАЦИИ ЗНАНИЙ.

МЕТОДЫ ОБУЧЕНИЯ:

ЧАСТИЧНО-ПОИСКОВЫЙ, ТЕСТОВАЯ ПРОВЕРКА УРОВНЯ ЗНАНИЙ, РЕШЕНИЕ ПОЗНАВАТЕЛЬНЫХ ОБОБЩАЮЩИХ ЗАДАЧ, СИСТЕМНЫЕ ОБОБЩЕНИЯ, САМОПРОВЕРКА.

ФОРМЫ ОРГАНИЗАЦИИ ТРУДА: ИНДИВИДУАЛЬНАЯ, ФРОНТАЛЬНАЯ.

ПЛАН УРОКА:

1. Орг. момент.

2. Устная работа.

3. Классификация тригонометрических уравнений.

4. Решение уравнений с дополнительными заданиями.

5. Самостоятельная работа.

6. Домашнее задание.

7. Итог урока.

1. Орг. момент.

Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело… Чтобы переварить знания, надо поглощать их с аппетитом». Давайте будем следовать этому совету писателя, будем активны, внимательны, всё будем делать с удовольствием и большим желанием.

Тема сегодняшнего урока «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы, методы и приёмы решения тригонометрических уравнений.

Перед вами задача – показать свои знания и умения по решению тригонометрических уравнений.

1. Устная работа.

1. Найти ошибки в ответах на предложенные вопросы.

Вопросы

1.Каково будет решение sin x=a, |a| 1?

2.При каком а уравнение sin x=a имеет решение?

3.Какой формулой выражается это решение?

4.В каком промежутке находится arcsin a?

5.В каком промежутке находится значение а?

6.Каким будет решение уравнения sin x=1?

7.Каким будет решение уравнения sin x=-1?

8.Каким будет решение уравнения sinx=0?

9.Чему равно arсsin(-a)?

10.В каком промежутке находится arcctg a?

11.Чему равно arcctg(-a)?

Ответы

1. Нет решения

2. |a|1

3.

4.

5.

6.

7.

8.

9. –arcsin a

10.

11. П – arcctg a

2. Письменно ответьте на вопросы, заменив sinx на cosx, ctgx на tgx.

После ответов, поменяйтесь работами и сверьте с доской, после чего поставьте соответствующую оценку.

Ответы (соs x, tgx)

1. Х = ±arccos a + 2πn, n Z

2. |a|1

3. Х = ±arccos a + 2πn, n Z

4. . [0; π]

5.

6. Х = 2πn, n Z

7. Х = π + 2πn, n Z

8. Х = π/2 + πn, n Z

9. П – arccos a

10.

11. – arctg a

1. Классификация тригонометрических уравнений.

Системно-обобщающая таблица.

№ 2,4,6,7,8,11 №1,5,10 №3,9,12

1.Решение алгебраических уравнений заключается в том, что все тригонометрические функции, которые входят в уравнение,

выражают какую-нибудь одну тригонометрическую функцию, зависящую от одного и того же аргумента.

2.Решение однородных уравнений (уравнения, в которых у всех слагаемых одинакова) и приводимых к ним сводится к решению алгебраических относительно tgx путём деления обеих частей уравнения на cosx≠0 и cos² x≠0 соответственно.

3. Решение с помощью разложения на множители сводится к решению двух элементарных уравнений.

ЗАДАНИЕ:

Определить тип тригонометрического уравнения:

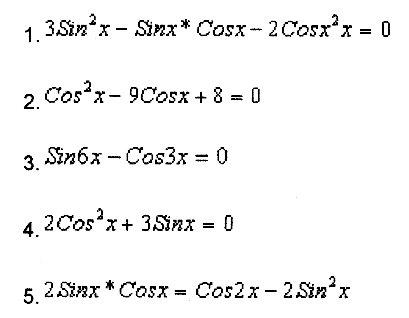
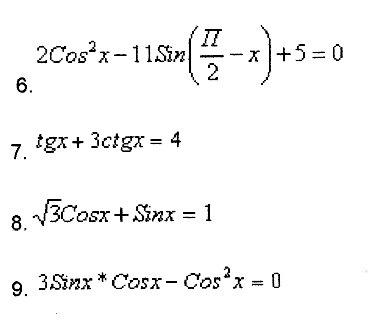
10. 1 – 3sinx*cosx – 5cos²x = 0

11. 2sin² 2x + 5sin2x – 3 = 0

12. sin5x + sinx = √2 sin3x

1. Решение уравнений.

Решение с указанием чёткого алгоритма решения уравнений данного типа.

1. Решить уравнение

Алгоритм:

1. Приведение к однородному уравнению.

2. Деление левой и правой части на Cos²x при условии Cosx0.

3. Решение квадратного уравнения.

4. Подстановка.

5. Решение простейших тригонометрических уравнений.

Ответ:

2. Найти наибольший отрицательный корень уравнения

Алгоритм:

1. Замена переменной.

2. Решение квадратного уравнения.

3. Решение простейших тригонометрических уравнений.

Ответ: Наибольший отрицательный корень

3. Найти сумму корней уравнения принадлежащих промежутку (0;П)

Найдем сумму

Дополнительно: Решить уравнение

Ответ:

ЗАРЯДКА ДЛЯ ГЛАЗ.

1. Тест. Самостоятельная работа.

Уровень В.

I вариант

1. Найти наименьший положительный корень уравнения

sinx + sin5x = 0.

А. π/6 Б. π/4

В. π /3 Г. π/2.

II вариант

1. Найдите наименьший положительный корень уравнения

cosx + cos5x = 0

А. π/6 В. π/4

Б. π/2 Г. π

1. Домашняя работа.

Домашняя работа выбирается самими обучающимися по уровням.

УРОВЕНЬ А.

УРОВЕНЬ В

VII. Итог урока.

• Чем мы занимались сегодня на уроке?

• Что за уравнения мы решали?

• Какие типы и методы решения мы знаем?

Устная работа по закреплению:

• Оценка работы класса.