Целые числа. Рациональные и иррациональные числа

Департамент охраны здоровья населения Кемеровской области Новокузнецкий филиал ГБПОУ «КОМК»

Целые числа. Рациональные и иррациональные числа

Шилепина Надежда Ивановна

преподаватель

Новокузнецк, 2019

Что такое число

Число  - основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.

Письменными знаками для обозначения служат цифры, а также символы математических операций.

02/10/2022

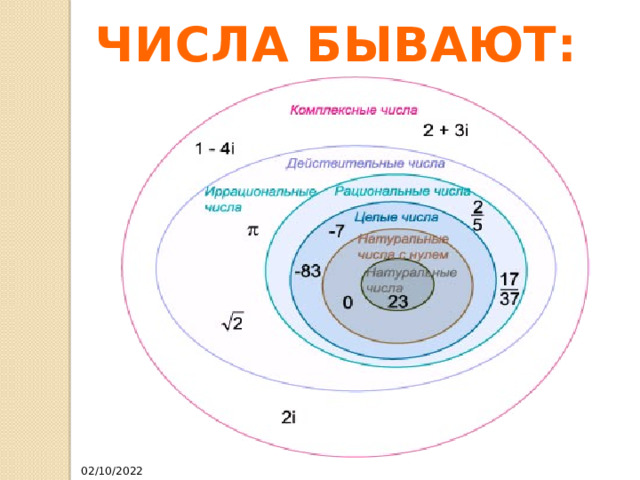
ЧИСЛА БЫВАЮТ:

02/10/2022

Натуральные числа

Для счета предметов используются числа, которые называются натуральными.

Для обозначения множества натуральных чисел употребляется буква  N  - первая буква латинского слова Naturalis, «естественный», «натуральный» (1, 2, 3, 4, 5, 6... )

02/10/2022

Целые числа

Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается  Z  - первой буквой немецкого слова Zahl - «число» ( …-3;-2;-1;0,1, 2, 3,...) .

02/10/2022

Сумма, произведение и разность целых чисел есть число целое.

Отрицательные числа ввели в математический обиход Михаэль Штифель (1487—1567) в книге «Полная арифметика» (1544), и Никола Шюке (1445—1500) - его работа была обнаружена в 1848 году.

02/10/2022

Действительные числа

Действительные числа не обладают свойством замкнутости - не всякое уравнение имеет корни. Действительные числа – это числа, которые могут быть записаны в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.

02/10/2022

Например: 5, 1056, π, … -это все действительные числа.

Действительные числа обозначают буквой R (рациональные числа, иррациональные числа)

02/10/2022

Рациональные числа

Множество чисел, которое можно представить в виде ,называется множеством рациональных чисел и обозначается - Q первой буквой французского слова Quotient - «отношение».

02/10/2022

Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью, где числитель m — целое число , а знаменатель n — натуральное число .

02/10/2022

Вычисли:

02/10/2022

Вычисли:

02/10/2022

Дробные числа

Десятичные дроби в XV веке ввел самаркандский ученый ал - Коши .

Второй раз, приблизительно через 150 лет, десятичные дроби открыл фламандский ученый математик и инженер Симон Стевин в труде « Децималь » (1585 г).

02/10/2022

Запомни

Чтобы обратить чисто периодическую дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде, а в знаменателе – написать цифру 9 столько раз, сколько цифр в периоде.

02/10/2022

Чтобы обратить смешанную периодическую дробь в обыкновенную , нужно в числителе обыкновенной дроби поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.

02/10/2022

Пример:

02/10/2022

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом.

Например:

02/10/2022

Иррациональные числа

Множество иррациональных чисел обычно обозначается заглавной латинской буквой I. Таким образом: I=R\Q , то есть множество иррациональных чисел есть  разность множеств вещественны чисел   и  рациональных  чисел.

02/10/2022

Самостоятельная работа

Представить дроби в виде быкновенных дробей:

15,(3)

0,(7)

1,2(3)

0,(12)

7,(5)

02/10/2022

Спасибо за внимание!!!

02/10/2022