Центральные и вписанные углы

Центральные и вписанные углы

Работу выполнил Малозёмов Артём 9 “В”

Историческая справка

Изложенное в современных учебниках доказательство того, что вписанный угол измеряется половиной дуги, на которую он опирается, дано в «Началах» Евклида. На это предложение ссылается, однако, еще Гиппократ Хиосский (V в. до н. э.) в своем труде о «луночках». Труды Гиппократа свидетельствуют о том, что уже во второй половине V в. до н. э. было известно большое число теорем, изложенных в «Началах» Евклида, и геометрия достигла высокого развития.

Евклид

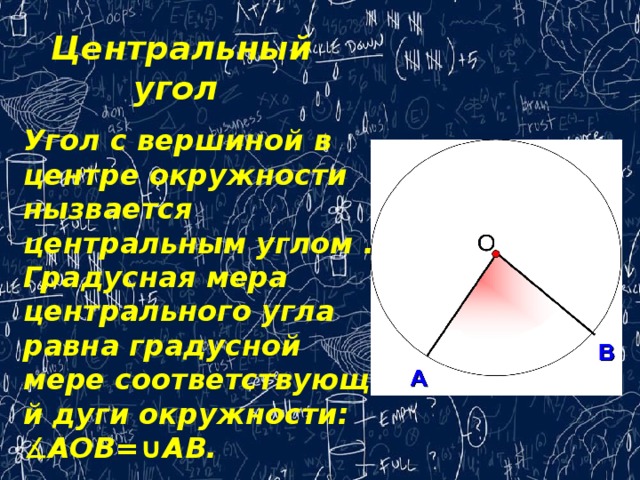
Центральный угол

Угол с вершиной в центре окружности нызвается центральным углом .

Градусная мера центрального угла равна градусной мере соответствующей дуги окружности: ∡ AOB=∪AB.

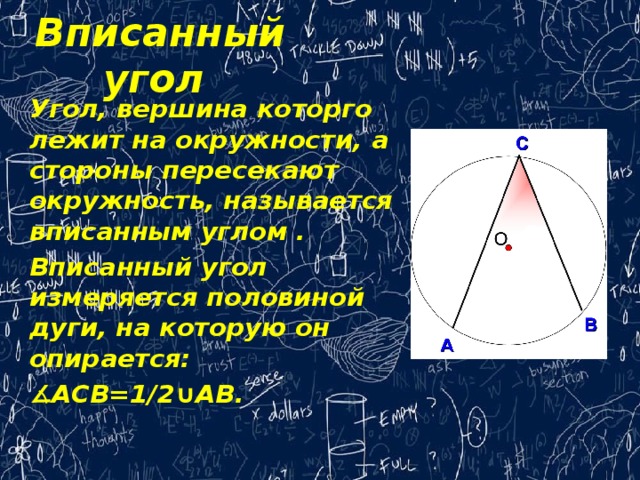
Вписанный угол

Угол, вершина которго лежит на окружности, а стороны пересекают окружность, называется вписанным углом .

Вписанный угол измеряется половиной дуги, на которую он опирается:

∡ ACB=1/2∪AB.

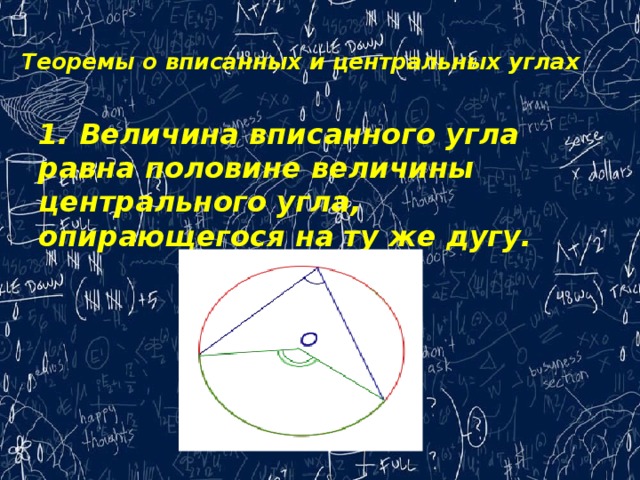
Теоремы о вписанных и центральных углах

1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

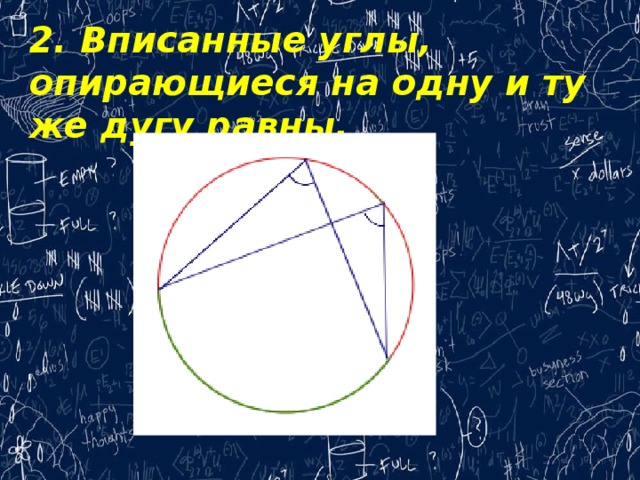
2. Вписанные углы, опирающиеся на одну и ту же дугу равны.

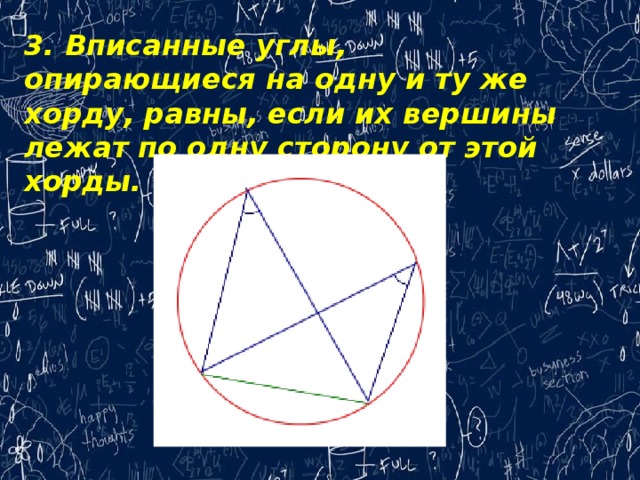
3. Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды.

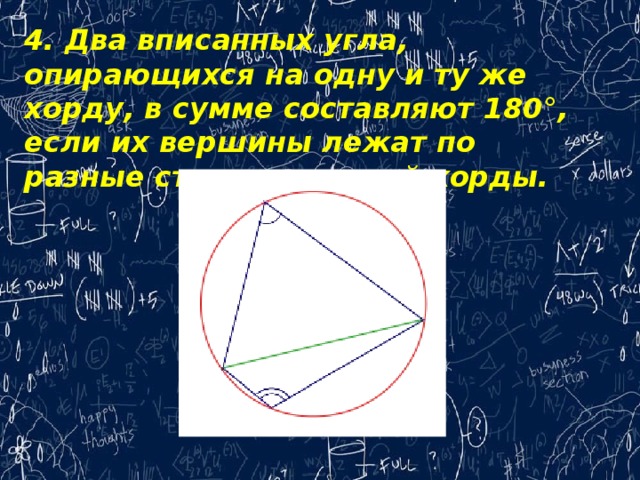
4. Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды.

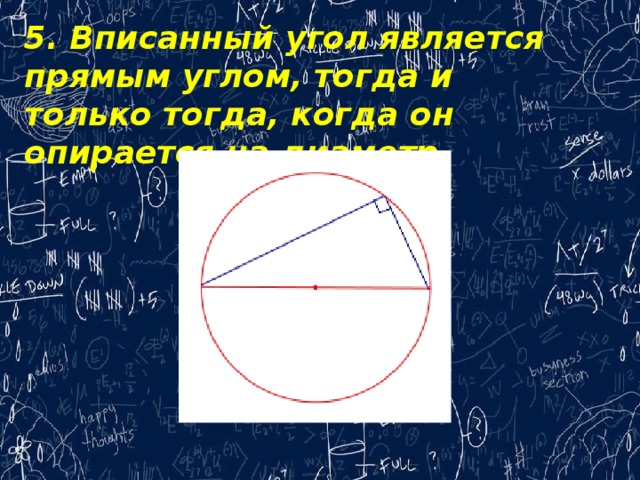
5. Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр.

Задачи

1.  Пусть O — центр окружности, описанной около треугольника ABC,

‍ ∠ AOC = 60‍∘.

‍  Найдите угол AMC,где M —

‍  центр окружности, вписанной в треугольник ABC.

‍

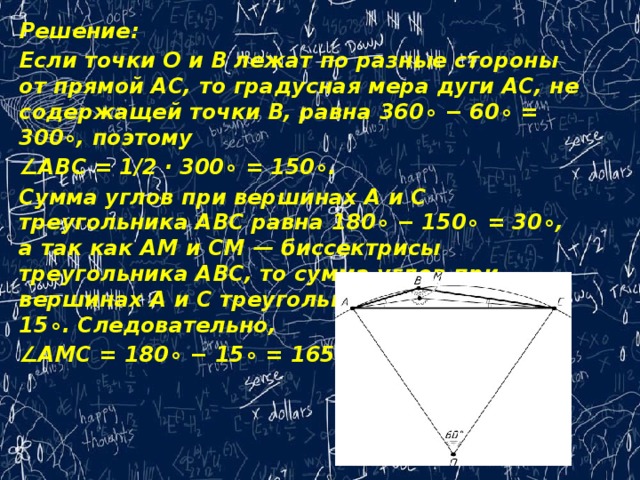
Решение:

Если точки O‍ и B‍ лежат по разные стороны от прямой AC‍, то градусная мера дуги AC,‍ не содержащей точки B,‍ равна 360‍∘ − 60‍∘ = 300‍∘,‍ поэтому

∠ ABC = ‍1/2 · 300‍∘ = 150‍∘.‍

Сумма углов при вершинах A‍ и C‍ треугольника ABC‍ равна 180‍∘ − 150‍∘ = 30‍∘,‍ а так как AM‍ и CM —‍ биссектрисы треугольника ABC,‍ то сумма углов при вершинах A‍ и C‍ треугольника AMC‍ равна 15‍∘.‍ Следовательно,

∠ AMC = 180‍∘ − 15‍∘ = 165‍∘.

2. Точки A и B делят окружность на две дуги, одна из которых равна 170∘, а другая точкой K делится в отношении 11:8, считая от точки A. Найдите ∠BAK. Ответ дайте в градусах.

Решение:

Т.к. ⌣ AK: ⌣ KB=11:8, то можно обозначить ⌣ AK=11x, ⌣ KB=8x.   Дуга ⌣ AKB=360∘−170∘=190∘. Следовательно, 11x+8x=19x=190∘⇒x=10∘. Значит, дуга ⌣ KB=8x=80∘. Угол BAK вписанный и опирается на эту дугу, следовательно, он равен ее половине, то есть 40∘.

Ответ: 40

3.Четырехугольник ABCD вписан в окружность. Угол ABC равен 105∘, угол CAD равен 35∘. Найдите угол ABD. Ответ дайте в градусах.

Решение:

Так как вписанный угол равен половине дуги, на которую он опирается, то ⌣ CDA=2⋅105∘=210∘. Аналогично меньшая дуга ⌣ CD=2⋅35∘=70∘ . Следовательно, меньшая дуга ⌣ AD=210∘−70∘=140∘ . Значит ∠ABD, как вписанный и опирающийся на дугу, равную 140∘, сам равен 70∘. Ответ: 70

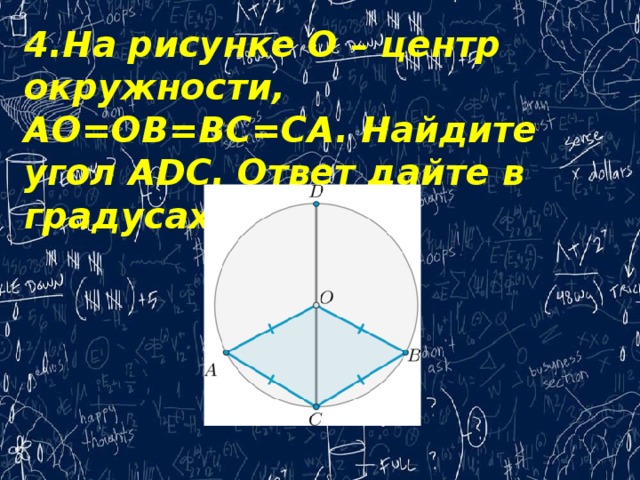
4.На рисунке O – центр окружности, AO=OB=BC=CA. Найдите угол ADC. Ответ дайте в градусах. 

Решение:

Четырехугольник, все стороны которого равны, является ромбом. Следовательно, AOBC – ромб. Значит, диагонали делят его углы пополам. Следовательно, ∠AOC=∠BOC=∠ACO=∠BCO=x.   Следовательно, ⌣ AC= ⌣ CB=x (т.к. на них опираются центральные углы AOC и BOC, равные этим дугам), ⌣ AD= ⌣ DB=2x (т.к. на них опираются вписанные углы ACD и BCD, равные половинам этих дуг). 

Т.к. вся окружность равна 360∘, то x+x+2x+2x=360∘⇒x=60∘.   Угол ADC – вписанный и опирающийся на дугу ⌣ AC, следовательно, он равен ее половине, то есть 30∘.

5.Секущая AB пересекает окружность и диаметр CD так, как показано на рисунке.

Меньшая дуга ⌣ KD равна 40∘, ∠CBA=30∘, прямая BC параллельна прямой AD. Найдите угол BTD. Ответ дайте в градусах. Показать решение

Решение:

Т.к. BC∥ AD, то ∠CBT=∠DAT=30∘. ∠DCK, как вписанный и опирающийся на дугу KD, равен ее половине, то есть 20∘. ∠CKD опирается на диаметр CD, следовательно, равен половине от половины окружности, то есть 90∘. Значит, ∠CDK=180∘−90∘−20∘=70∘.   ∠BTD — внешний угол для треугольника ATD, следовательно, он равен сумме двух углов треугольника, не смежных с ним: ∠BTD=∠TDA+∠TAD=30∘+70∘=100∘.

Ответ: 100

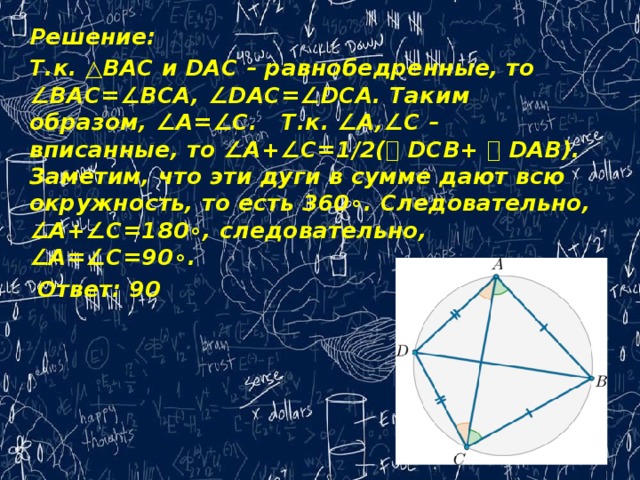
6.На окружности в следующем порядке отмечены четыре точки: A, B, C и D, причем AB=BC, CD=DA. Найдите угол BAD. Ответ дайте в градусах.

Решение:

Т.к. △BAC и DAC – равнобедренные, то ∠BAC=∠BCA, ∠DAC=∠DCA. Таким образом, ∠A=∠C.   Т.к. ∠A,∠C – вписанные, то ∠A+∠C=1/2(⌣ DCB+ ⌣ DAB). Заметим, что эти дуги в сумме дают всю окружность, то есть 360∘. Следовательно, ∠A+∠C=180∘, следовательно, ∠A=∠C=90∘.

Ответ: 90

Источники

1) https ://shkolkovo.net/catalog/planimetriya_chast_ii/okruzhnost_centralnye_i_vpisannye_ugly/page-2

2) https ://www.resolventa.ru/spr/planimetry/cangle.htm

3) https ://egemaximum.ru/vpisannye-ugly /

Учебник по геометрии 7-9 класс авторы: Л.С.Атанасян,В.Ф.Бутузов и т.д.