Центральные и вписанные углы

Центральные и вписанные углы

Геометрия, 8 класс

К учебнику Л.С.Атанасяна

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

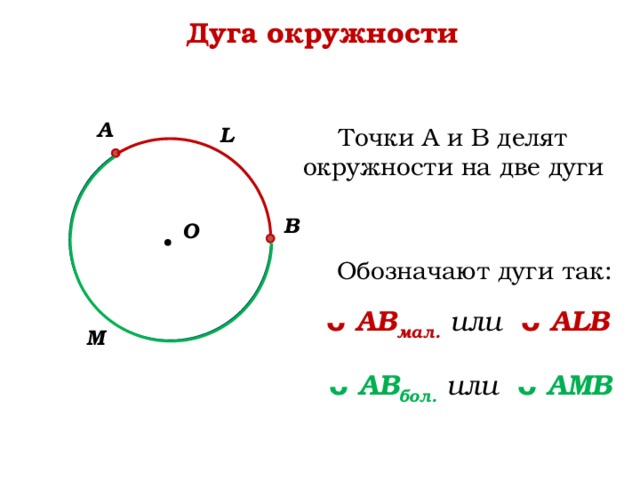
Дуга окружности

А

L

Точки А и В делят окружности на две дуги

В

О

Обозначают дуги так:

ᴗ АВ мал. или ᴗ АLВ

М

ᴗ АВ бол. или ᴗ АМВ

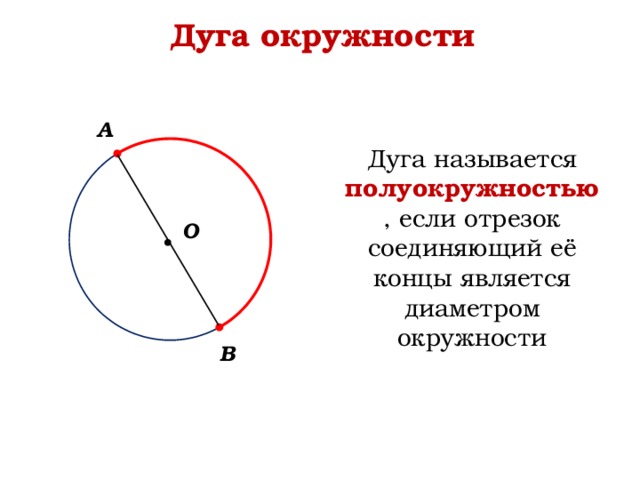
Дуга окружности

А

Дуга называется полуокружностью , если отрезок соединяющий её концы является диаметром окружности

О

В

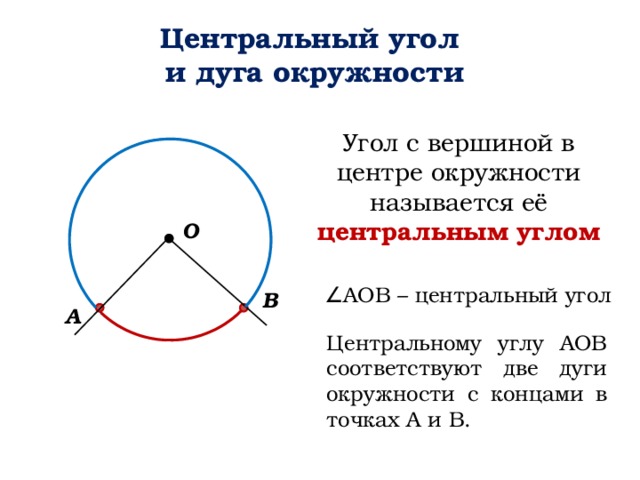
Центральный угол

и дуга окружности

Угол с вершиной в центре окружности называется её центральным углом

О

∠ АОВ – центральный угол

В

А

Центральному углу АОВ соответствуют две дуги окружности с концами в точках А и В.

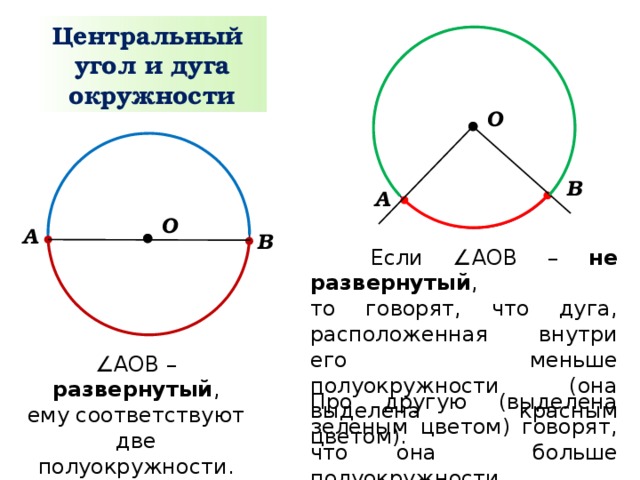
Центральный

угол и дуга окружности

О

В

А

О

А

В

Если ∠АОВ – не развернутый ,

то говорят, что дуга, расположенная внутри его меньше полуокружности (она выделена красным цветом).

∠ АОВ – развернутый ,

ему соответствуют две полуокружности.

Про другую (выделена зеленым цветом) говорят, что она больше полуокружности.

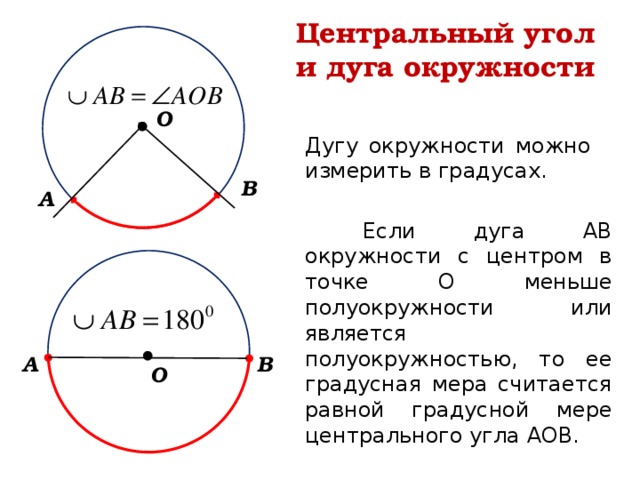
Центральный угол и дуга окружности

О

Дугу окружности можно измерить в градусах.

В

А

Если дуга АВ окружности с центром в точке О меньше полуокружности или является полуокружностью, то ее градусная мера считается равной градусной мере центрального угла АОВ.

В

А

О

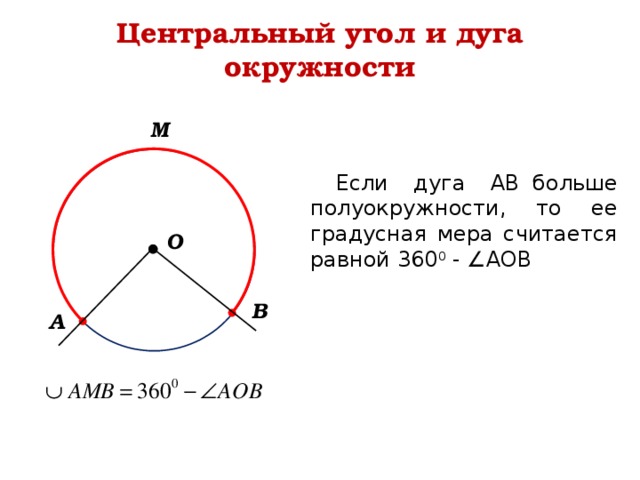
Центральный угол и дуга окружности

М

Если дуга АВ больше полуокружности, то ее градусная мера считается равной 360 0 - ∠АОВ

О

В

А

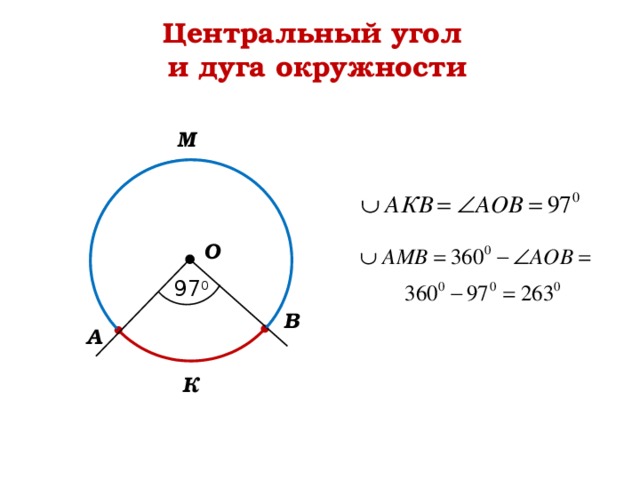
Центральный угол

и дуга окружности

М

О

97 0

В

А

К

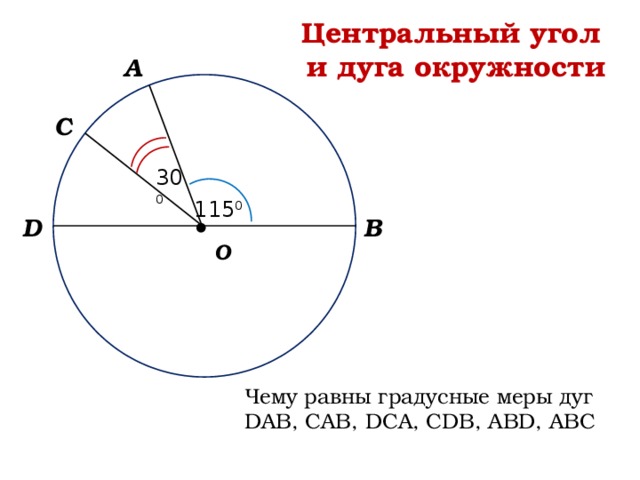
Центральный угол

и дуга окружности

А

С

30 0

115 0

В

D

О

Чему равны градусные меры дуг

DAB, САВ, DCA, CDB, ABD, ABC

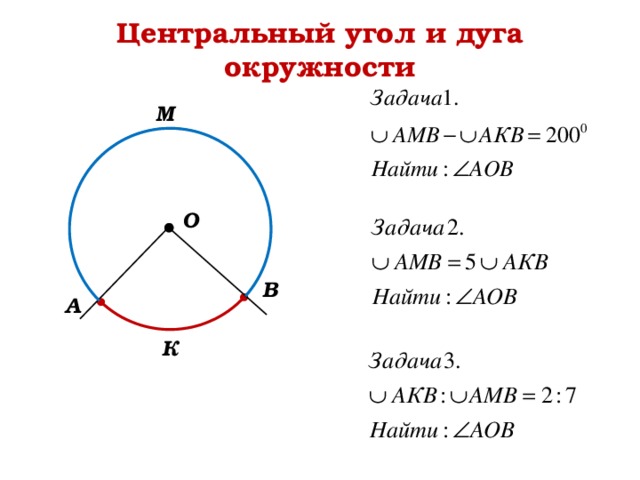
Центральный угол и дуга окружности

М

О

В

А

К

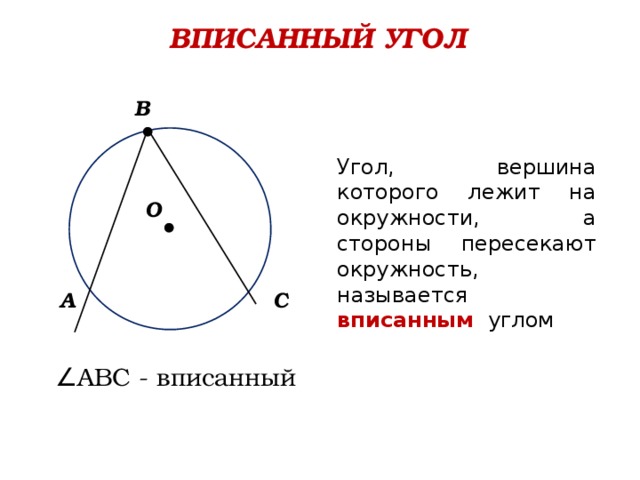
ВПИСАННЫЙ УГОЛ

В

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом

О

А

С

∠ АВС - вписанный

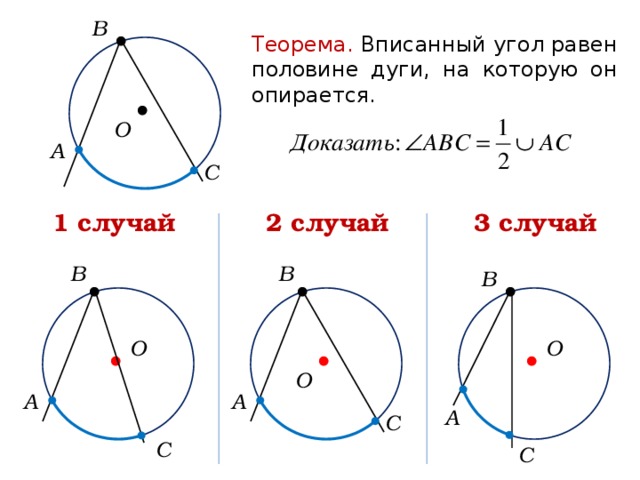
В

Теорема. Вписанный угол равен половине дуги, на которую он опирается.

О

А

С

2 случай

3 случай

1 случай

В

В

В

О

О

О

А

А

А

С

С

С

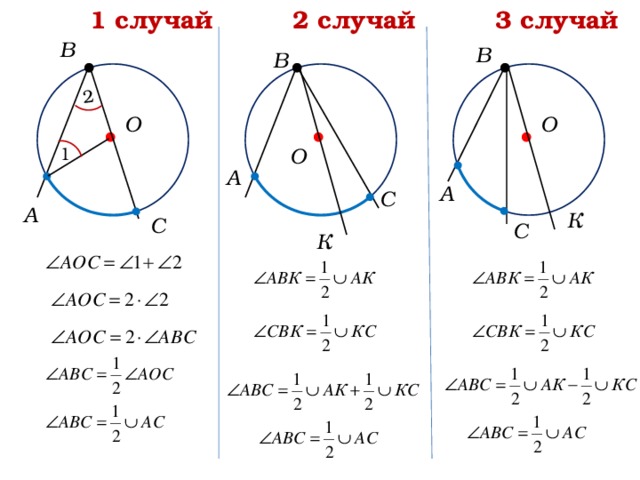
3 случай

2 случай

1 случай

2

В

В

В

О

О

О

1

А

А

С

А

К

С

С

К

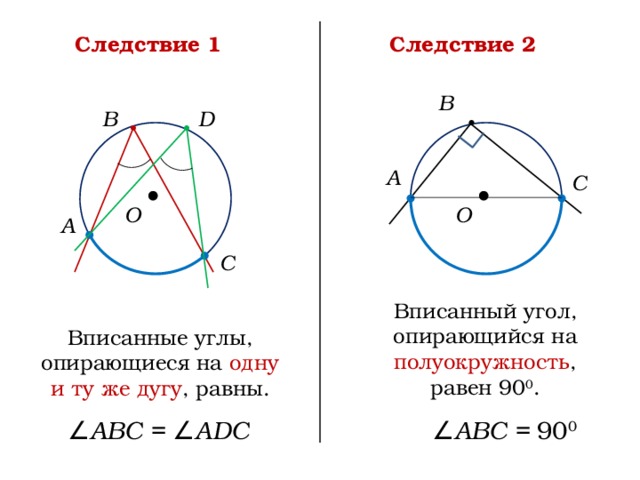
Следствие 1

Следствие 2

В

D

В

А

С

О

О

А

С

Вписанный угол, опирающийся на полуокружность , равен 90 0 .

Вписанные углы, опирающиеся на одну и ту же дугу , равны.

∠ АВС = ∠АDС

∠ АВС = 90 0

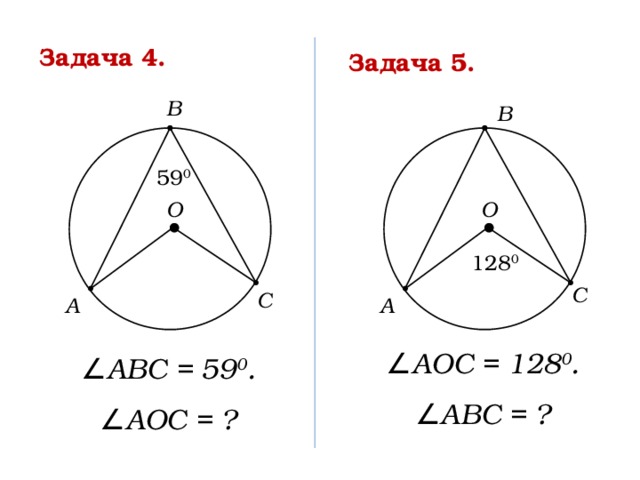
Задача 4.

Задача 5.

В

В

59 0

О

О

128 0

С

С

А

А

∠ АОС = 128 0 .

∠ АВС = ?

∠ АВС = 59 0 .

∠ АОС = ?

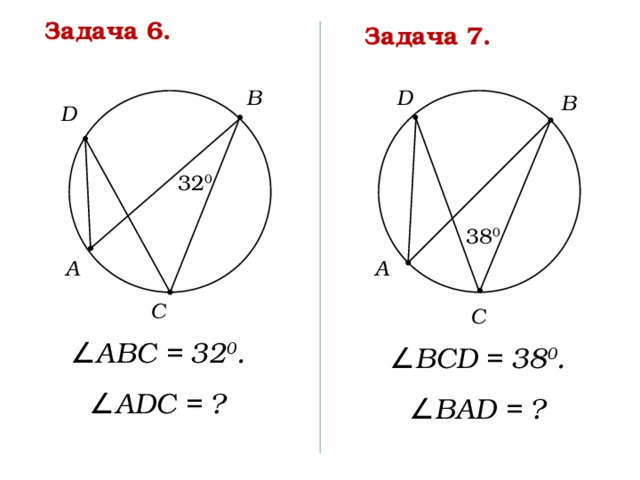
Задача 6.

Задача 7.

В

D

В

D

32 0

38 0

А

А

С

С

∠ АВС = 32 0 .

∠ АDС = ?

∠ BCD = 38 0 .

∠ BAD = ?

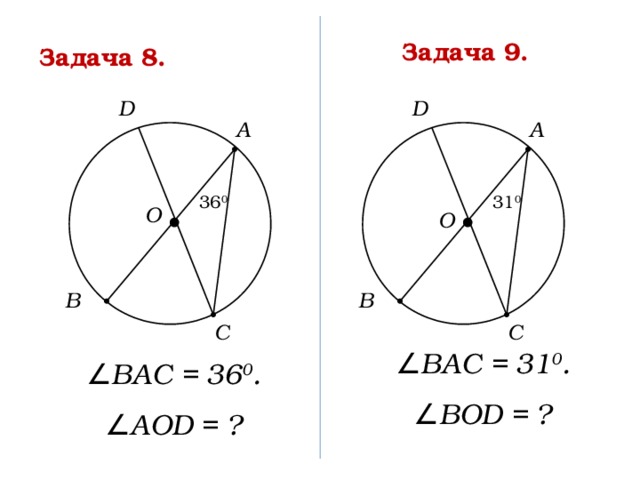
Задача 9.

Задача 8.

D

D

А

А

31 0

36 0

О

О

В

В

С

С

∠ BAC = 31 0 .

∠ BOD = ?

∠ BAC = 36 0 .

∠ АОD = ?

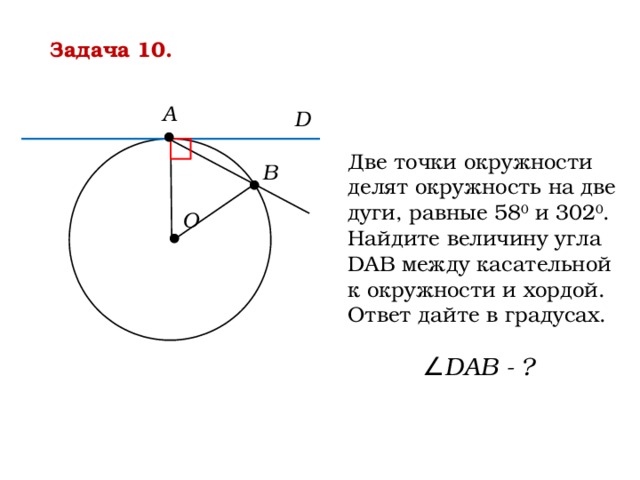
Задача 10.

А

D

Две точки окружности делят окружность на две дуги, равные 58 0 и 302 0 . Найдите величину угла DAB между касательной к окружности и хордой. Ответ дайте в градусах.

В

О

∠ DАВ - ?

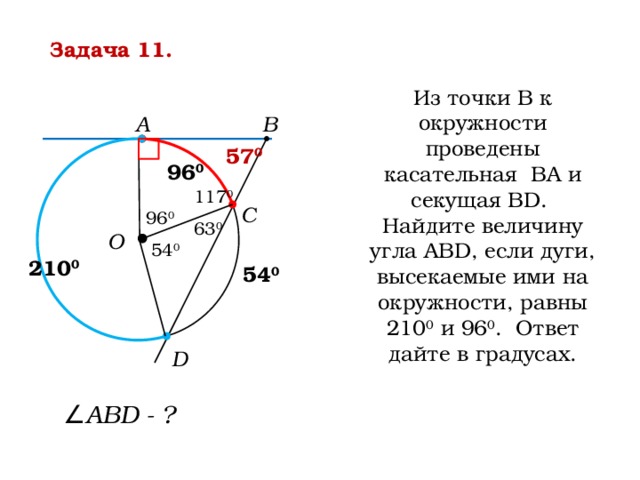
Задача 11.

Из точки В к окружности проведены касательная ВА и секущая ВD.

Найдите величину угла АВD, если дуги, высекаемые ими на окружности, равны 210 0 и 96 0 . Ответ дайте в градусах.

А

В

57 0

96 0

117 0

С

96 0

63 0

О

54 0

210 0

54 0

D

∠ АВD - ?

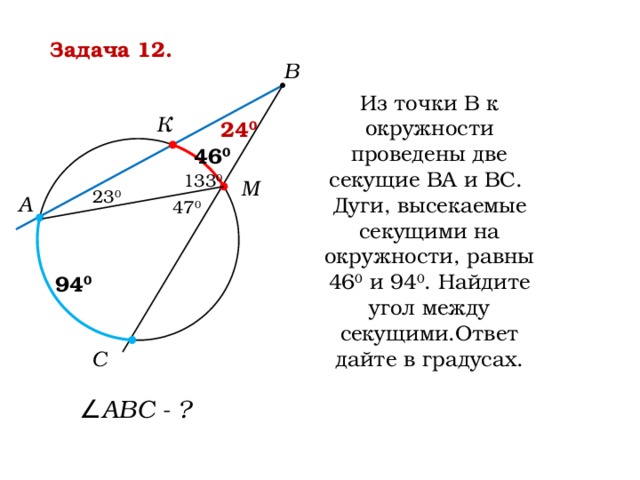
Задача 12.

В

Из точки В к окружности проведены две секущие ВА и ВС.

Дуги, высекаемые секущими на окружности, равны 46 0 и 94 0 . Найдите угол между секущими.Ответ дайте в градусах.

К

24 0

46 0

133 0

М

23 0

А

47 0

94 0

С

∠ АВС - ?

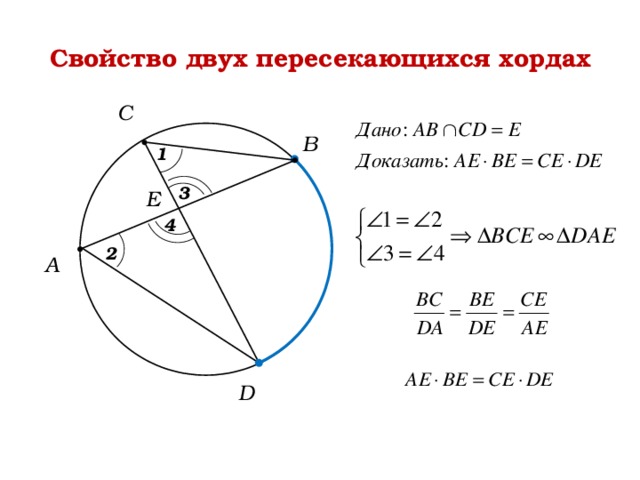
Свойство двух пересекающихся хордах

С

В

1

3

Е

4

2

А

D

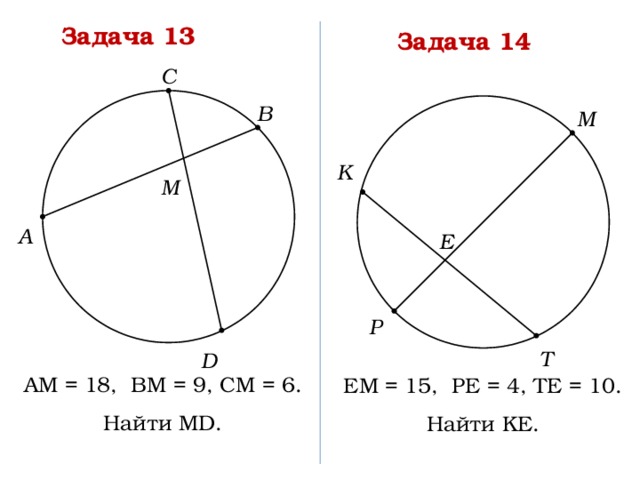
Задача 13

Задача 14

С

В

М

K

М

А

E

P

T

D

АМ = 18, ВМ = 9, СМ = 6.

Найти МD.

EМ = 15, PE = 4, TE = 10.

Найти KE.

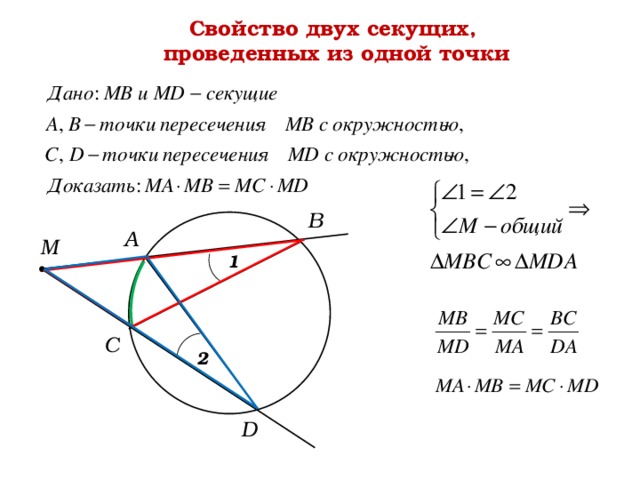
Свойство двух секущих,

проведенных из одной точки

В

А

М

1

С

2

D

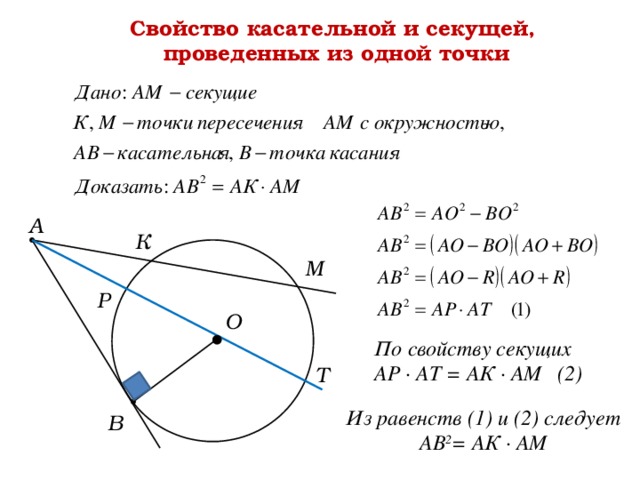
Свойство касательной и секущей,

проведенных из одной точки

А

К

М

Р

О

По свойству секущих

АР ∙ АТ = АК ∙ АМ (2)

Т

Из равенств (1) и (2) следует

АВ 2 = АК ∙ АМ

В