Удивительное число П

Удивительное число π

Автор работы:

Жиганова Алёна Сергеевна

10а класс, МОУ «Средняя общеобразовательная школа №3»

г. Балаково, Балаковский район

Руководитель:

Вайланд Анна Павловна

учитель математики, МОУ «Средняя общеобразовательная школа №3» г. Балаково,

Балаковский район

Балаково, 2011

Число  - что это?

• Число  - математическая константа
• Число  - это число, которое равно отношению длины окружности к ее диаметру.

Цели исследования

• Цель работы - на историческом материале показать возможность и необходимость проблемы вычисления числа π, раскрыть вездесущность геометрического символа, показать огромное трудолюбие и работоспособность ученых, занимавшихся этим вопросом в течение многих столетий.
• В работе описаны основные исторические события, связанные с открытием использованием числа π, а также использование его в современном мире и применение числа к различным сферам науки и жизнедеятельности человека.
• В работе исследовано, что :
• для измерения числа π можно воспользоваться взвешиванием
• объем купола храма примерно 3 раза укладывается во всем объеме храма
• отношение размаха рук человека к его росту равно 1,03.

• С чего всё начиналось ?

• Открывателями числа π можно считать людей доисторического времени, которые при плетении корзин заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его.
• Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт.

История числа 

• Письменная история числа  начинается с египетского папируса, датируемого примерно 2000 годом до нашей эры, но оно было известно ещё древним людям.
• Число  обратило на себя внимание людей ещё в те времена, когда они не умели письменно излагать ни своих знаний, ни своих переживаний, ни своих воспоминаний.

Обозначение числа 

• Обозначение числа «Пи» происходит от греческого слова perijerio «периферия», что означает «окружность».
• Впервые это обозначение использовал в 1706 году английский математик Уильям Джонс, но общепринятым оно стало после того, как его стал систематически употреблять Леонард Эйлер, начиная с 1736 года

Вавилон и число 

• Как считают специалисты, это число было открыто вавилонскими магами. Вавилоняне пользовались лишь грубым приближением, определив  числом «3».
• Число  использовалось при строительстве знаменитой Вавилонской башни, но недостаточно точное исчисление значения  привело к краху всего проекта.

«Архимедово число»

Идею заменить длину окружности периметром описанного (вписанного) многоугольника применил Архимед ( III век до н.э.).

Начав с 6-угольника, перешел к 12-угольнику, затем к 24 угольнику, и так далее – до 96-угольника.

Хорошее приближение

оказалось дает число

22 / 7  3,14286

Греция, 22/7  3,1428

• Архимед доказал, что число "пи" одинаково для любого круга.
• Математический метод Архимеда подводил к познанию геометрической формы, к которой предметы более или менее приближаются, и законы которой необходимо знать, если мы хотим воздействовать на материальный мир.
• В Древней Греции появилась архитектура, а где архитектура – там и расчеты.

Египет, 49/16  3,1604

• Великая Пирамида является

фантастическим шедевром инженерного искусства не только благодаря своим гигантским размерам

• Основание Пирамиды, покоящееся на гранитной поверхности, представляет собой почти идеальный квадрат (максимальное отклонение 3 минуты 33 секунды) со сторонами около 230 метров.

Китай, 355/113  3,14159

• Высокого расцвета достигла в Китае вычислительная техника, основанная на приближенных вычислениях.
• Примером служит приближенное вычисление отношения длины окружности к ее диаметру китайским математиком Цзу Чун-чжи (430-501), который для  получил приближение 355/113, дающее 7 верных значащих цифр, и показал, что число  лежит в пределах: 3,1415296

Индия, 377 / 120  3,162

• Арьябхатта (родился 476 г.н.э.) нашел точное значение 3,1416 или 62832 / 20000.
• Число 377 / 120 вычислил Будхайян. Он также в 6 веке дал варианты действий того, что известно как Теорема Пифагора.
• Число 3927 / 1250 вычислил Бхаскара (родился в 1114 г.н.э.) вычислил число  .

Россия и число 

• У наших предков не было компьютеров, калькуляторов и справочников, но со времен Петра I они занимались геометрическими расчетами в астрономии, в машиностроении, в корабельном деле, в электротехнике.
• Для запоминания числа "Пи" было придумано двустишие. В учебнике Л.Ф.Магницкого «Арифметика» оно написано по правилам старой русской орфографии, по которой после согласной в конце слова обязательно ставился "мягкий" или "твердый" знак.

Кто и шутя, и скоро пожелаетъ

"Пи" узнать число - ужъ знаетъ.

Тысячелетняя гонка

• На протяжении всей истории изучения числа  , вплоть до наших дней, велась своеобразная погоня за десятичными знаками этого числа.
• Леонардо Фибоначчи (около 1220 г.) определил три первых точных знака числа  .

Погоня за знаками

1) Андриан Антонис - 6 точных десятичных знаков (в XVI в.);

2) Цзу Чун-чжи (Китай) – 7 десятичных знаков ( V в.н.э.);

3) Франсуа Виет – 9 десятичных знаков;

4) Андриан ван Ромен – 15 десятичных знаков (1593г.);

5) аль-Каши – 17 знаков после запятой ( XV в.)

6) Лудольф ван Келён – 20 десятичных знаков;

7) Лудольф ван Цейлену – 32 десятичных знаков (1596г.);

В его честь число  было названо современниками " Лудольфово число ".

8) Авраам Шарп – 72 десятичных знаков

9) Джон Мечин – 100 десятичных знаков (1706 г.)

10) З. Дазе – 200 десятичных знаков (1844г.)

11) Т. Клаузен – 248 десятичных знаков (1847г.)

12) Рихтер - 330 знаков, З. Дазе - 440 знаков и У.Шенкс – 513

знаков (1853г.)

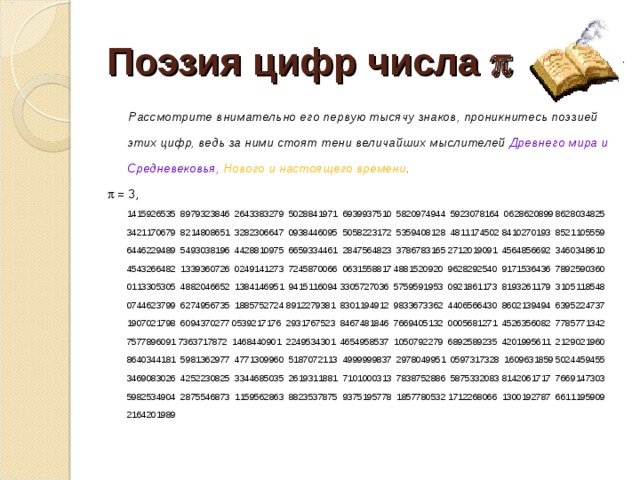
Поэзия цифр числа 

Рассмотрите внимательно его первую тысячу знаков, проникнитесь поэзией этих цифр, ведь за ними стоят тени величайших мыслителей Древнего мира и Средневековья, Нового и настоящего времени .

 = 3, 1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989

Компьютер и число 

• 1949 год — 2037 десятичных знаков
• 1958 год — 10000 десятичных знаков
• 1961 год — 100000 десятичных знаков
• 1973 год — 10000000 десятичных знаков
• 1986 год — 29360000 десятичных знаков
• 1987 год — 134217000 десятичных знаков
• 1989 год — 1011196691 десятичный знак
• 1991 год — 2260000000 десятичных знаков
• 1994 год — 4044000000 десятичных знаков
• 1995 год — 4294967286 десятичных знаков
• 1997 год — 51539600000 десятичных знаков
• 1999 год — 206158430000 десятичных знаков.

Японские ученые вычислили число Пи с рекордной точностью, сообщает издание The Mainichi Daily News. Новый рекорд составляет 2576980377524 (2 триллиона 576 миллиардов 980 миллионов 377 тысяч 524) знака. Для рекордного вычисления ученые использовали суперкомпьютер T2K Tsukuba System, который работал более 73 часов. Этот компьютер способен выполнять 95 миллиардов операций с плавающей точкой в секунду. В настоящее время исследователи подали заявку на включение своего достижения в Книгу рекордов Гиннесса.

День рождения числа 

• 3.14 или 22. 7 (день приближенного значения  ) «Отцом» праздника стал Ларри Шоу в 1998 г. в музее Эксплораториуме (Сан-Франциско) устроили праздник числа 

Эта дата совпала

с днем рождения

Альберта Эйнштейна –

выдающегося ученого

ХХ столетия.

Измерение значения  с помощью взвешивания

• На листе картона начертим квадрат. Впишем в него круг. Вырежем квадрат. Определим массу картонного квадрата с помощью весов. Вырежем из квадрата круг. Взвесим его. Зная массу квадрата m кв , воспользуемся формулами m=pV, V=Sh, где p и h – плотность и толщина картона, S – площадь фигуры.
• Рассмотрим равенства:
• m кв = pS кв h=p4R 2 h
• m кр = pS кр h=pπR 2 h

• Следовательно

Измерение значения  с помощью взвешивания

Число π в строительстве храмов

Используя чертежи строящегося в Балаково храма (по ул. Набережная Леонова; ост. «Строительная»), предоставленные отцом Николаем я заметила, что объем купола храма примерно 3 раза укладывается во всем объеме храма. Другими словами, объём купола укладывается примерно с коэффициентом 3,14 в сравнении с полным объёмом храма. Это придаёт устойчивость и гармоничность храму

Число  и «золотое сечение»

Золотая пропорция – деление отрезка на две неравные части так, что длина большей части превышает длину меньшей части ровно во столько раз, во сколько раз весь отрезок превышает длину большей части.

Число Фидия Ф =

Отношение размаха рук человека

к его росту равно = 1,03…

Число  и «золотое сечение»

В процессе исследования я сделала следующие измерения одноклассницы:

- рост - 165 см.

- размах рук – 162 см.

Отношение размаха рук к росту

в этом случае получилось:

Отсюда:

Число «Пи» в картинках

Вывод

• Несмотря на огромное трудолюбие и работоспособность ученых, занимавшихся этим вопросом в течение многих столетий, загадочное и вездесущное число «Пи» ещё наверняка хранит массу секретов и тайн.

,

Используемые источники

• 1. Глейзер Г. История математики в школе, 1982.
• 2. «Наука и жизнь», № 11/79.
• 3. «Квант»; № а) 4/87; б) 7/89; в) 9/89.
• 4. «Математика в школе»: а) № 5/88; б) № 4/91.
• 5. Энциклопедический словарь юного математика. 6. Интернет-сайт: http :// www . lenta . ru
• 7. Интернет-сайт http ://www.calend.ru