Углубленное изучение курса математики 10 класса. Матрица системы линейных уравнений

Муниципальное бюджетное общеобразовательное учреждение

«Гимназия №2» г. Курчатова

УГЛУБЛЁННОЕ ИЗУЧЕНИЕ КУРСА МАТЕМАТИКИ 10 КЛАССА.

МАТРИЦА СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Курчатов, 2024

Введение

• Система уравнений - это условие, состоящее в одновременном выполнении нескольких уравнений относительно нескольких (или одной) переменных .

• Решением системы уравнений являются такие значения неизвестных, при подстановке которых каждое уравнение системы обращается в верное равенство.

.

Актуальность :

• В наше время от умения эффективно решать системы линейных уравнений часто зависит сама возможность математического моделирования самых разнообразных процессов с применением искусственного интеллекта и нейронных сетей. Значительная часть численных методов решения различных задач включает в себя решение систем линейных уравнений. Алгоритмы решения систем уравнений играют заметную роль в инженерии, физике, химии, информатике и экономике.

Основная часть

Глава I

Теоретическая часть

1.1 Системы линейных уравнений с тремя неизвестными.

Системы линейных уравнений с тремя неизвестными имеют вид:

Где a, b, c, d, e, f, g, h, p, q, r, s – заданные числа; x, y, z – неизвестные. Числа a, b, c, e, f, g, p, q, r – коэффициенты при неизвестных; d, h, s – свободные члены.

1.2. Методы решения систем уравнений с тремя переменными.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.

1.2.1 Метод Гаусса

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Назван в честь немецкого математика Карла Фридриха Гаусса. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно находятся все переменные системы .

Карл Фридрих Гаусс

1777-1855

Рассмотрим систему уравнений и решим её методом Гаусса:

1.2.2 Матричный метод

• Матрица – совокупность чисел или других математических объектов, расположенных в виде прямоугольной таблицы и упорядоченных с помощью индексов. Под другими объектами понимают векторы, функции и т. п.
• При решении систем линейных уравнений можно не использовать переменные, а ограничиться табличкой из коэффициентов:

• - матрица системы линейных уравнений
• - расширенная матрица

Рассмотрим ту же систему, с которой работали, применяя метод Гаусса, только сейчас решим её матричным методом.

• Вернемся к системе:

• И решим её всем известным способом.

1.2.3 Метод Крамера

• Ме́тод Крамера (правило Крамера) — способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы (причём для таких уравнений решение существует и единственно)

Габриэль Крамер

1704г-1752г

Формулы Крамера

• ОПРЕДЕЛИТЕЛЬ - или детерминант, - в математике запись чисел в виде квадратной таблицы, в соответствие которой ставится другое число

1) - матрица второго порядка

Δ = = - - определитель этой матрицы

2) - матрица третьего порядка

Δ ==

- определитель этой матрицы

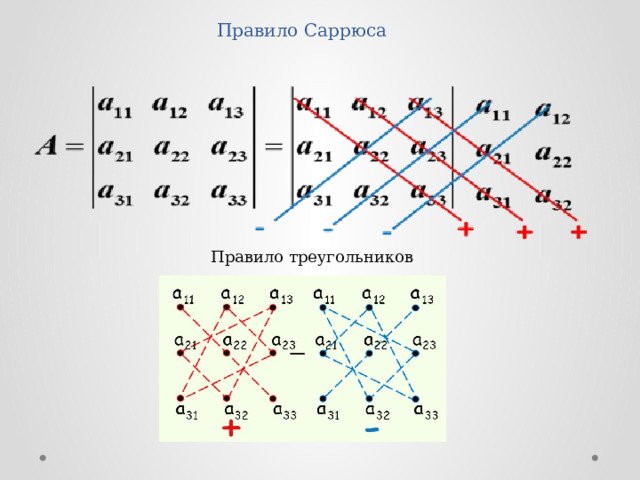
Правило Саррюса

Правило треугольников

Минор

• Минором какого либо элемента называется определитель, получаемый из данного определителя вычеркиванием той строки и того столбца, на пересечении которых стоит данный элемент.

Алгебраическим дополнением элемента называется его минор, взятый со своим или противоположным знаком. согласно следующему правилу: если сумма номеров столбца и строки, на пересечении которых стоит элемент, есть число четное, то минор берется со своим знаком, если нечетное – то с противоположным.

Примеры вычисления определителей

2.2 Практическое применение решения систем уравнений с тремя переменными.

Предприятие производит следующие изделия: перчатки, сумки и портмоне. Для производства используется сырье 3-х видов. Известен расход сырья на единицу изделия и объем расхода сырья на 1 неделю (заданы в таблице). Необходимо найти еженедельный объем выпускаемой продукции каждого вида.

x – это объем производства перчаток

y – объем производства сумок

z - объем производства портмоне.

составим систему уравнений:

перчатки

Сырье 1

сумки

6

Сырье 2

портмоне

1

2

Сырье 3

3

0

Расход на 1 неделю

0

1

280

2

60

4

310