Умножение и деление степеней

Проверка домашней работы

5 2 + 3 3 =

(25 – 15) 2 =

2 ·(-3) 2 + 5 · 2 4 =

52

Выполните действия:

100

98

64 =

144 =

1 0000 =

8 2

Представьте в виде квадрата число:

12 2

100 2

Умножение и деление степеней

«Пусть кто-нибудь попробует вычеркнуть из математики

степени, и он увидит, что без них далеко не уедешь» М.В. Ломоносов

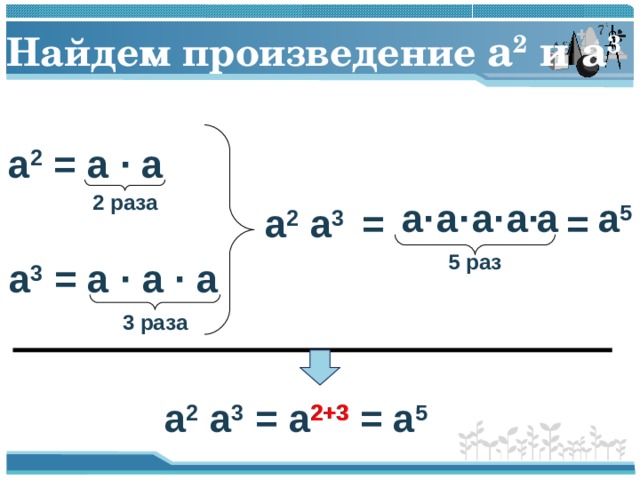
Найдем произведение a 2 и a 3

a 2 = a · a

2 раза

a·

a·

a·

a·

a

a 5

a 2 a 3 =

=

5 раз

a 3 = a · a · a

3 раза

a 2 a 3 = a 2+3 = a 5

2+3

• Основное свойство степени

Для любого числа a и

произвольных натуральных

чисел m и n

a m a n = a m+n

Правило умножения степеней

a m · a n · a k = a (m+n) ·a k = a m+n+k

При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают

Примеры:

Выбираем правильный ответ

Молодцы!

Решаем в парах

• а 17 · а 23 =
• d 4 · d 6 =
• b 4 · b 11 =
• c 12 · c 13 =
• k 3 · k 34 =
• h 32 · h 21 =
• g 24 · g 13 =

а 40

d 10

b 15

c 25

k 37

h 53

g 3 7

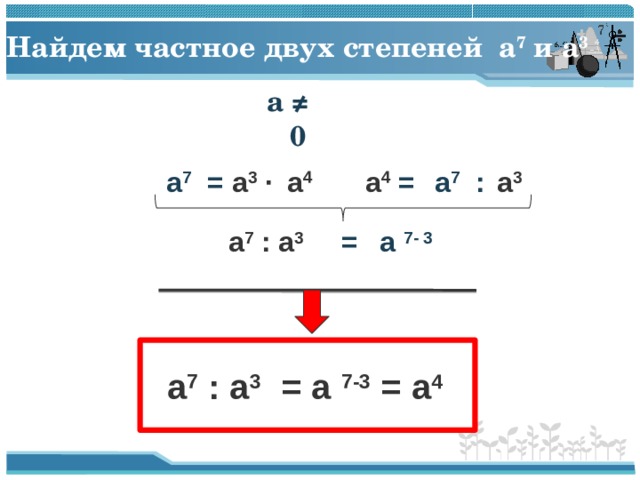
Найдем частное двух степеней a 7 и a 3

a ≠ 0

a 7 =

a 3 ∙

a 4

a 4 =

a 3

a 7 :

=

a 7 - 3

a 7 : a 3

a 7 : a 3 = a 7-3 = a 4

n , a m : a n = a m-n " width="640"

a m : a n = a m-n

• свойство степени

Для любого числа a ≠ 0 и произвольных натуральных чисел m и n , таких, что m n ,

a m : a n = a m-n

Правило деления степеней

При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры:

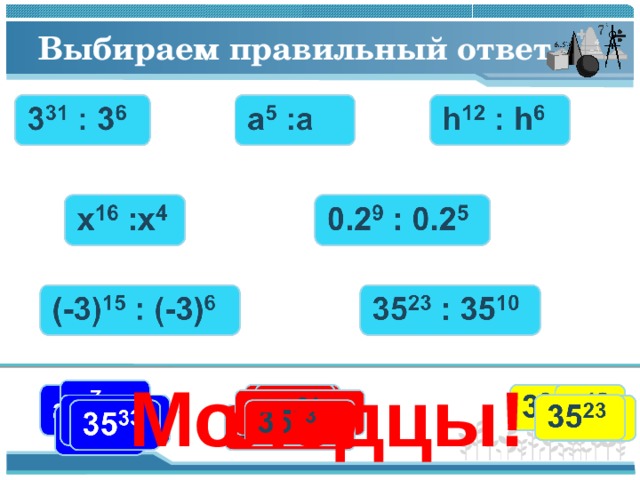
Выбираем правильный ответ

Молодцы!

Определение степени с нулевым показателем

При a ≠ 0

Степень числа a , не равного нулю,

с нулевым показателем равна единице.

Физкультминутка

выражение меньше нуля – корпус

выражение больше нуля - корпус

(-2) 3

-4 6

(-23) 2

(-8) 11

-(-15) 4

7 8

(-8) 6

Проверочная работа

Представить в виде степени:

Вариант I

Вариант II

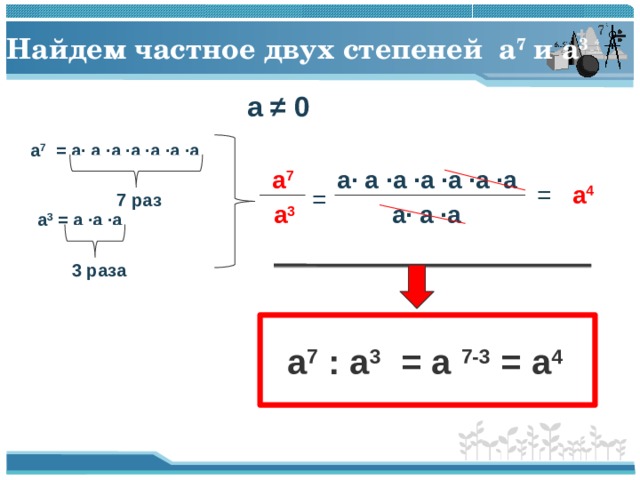
Найдем частное двух степеней a 7 и a 3

a ≠ 0

a 7 = a· a ·a ·a ·a ·a ·a

a· a ·a ·a ·a ·a ·a

a 7

=

a 4

=

7 раз

a 3

a· a ·a

a 3 = a ·a ·a

3 раза

a 7 : a 3 = a 7-3 = a 4