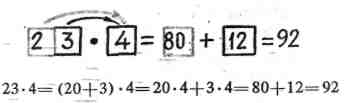Умножение и деление в пределах 100

1.Смысл действия умножения.

Работа над этим начинается еще в 1 классе при изучении нумерации, сложения и вычитания в пределах 10 и 100:

Упражнения:

• счет предметов парами, тройками….

• решение задач на нахождение суммы одинаковых и неодинаковых слагаемых.

• составление рисунков к задачам или составление задач по рисункам.

Во II классе дети знакомятся с действием умножения.

На конкретном материале можно детям предложить задачу, для решения которой нужно найти сумму одинаковых слагаемых.

Например: в трех коробках лежало по 6 карандашей в каждой. Сколько всего карандашей в коробках?

Выполнив иллюстрацию, дети записывают решение действием сложения:

6 + 6 + 6 = 18 (к).

Учитель:

-Что можно сказать о слагаемых? (одинаковые)

-Сколько их? (здесь взяли по 6 три раза)

Если слагаемые одинаковые, то сумму можно записать иначе: 6 * 3 = 18.

Чтение: по 6 взять три раза = 18. 6 умножить на 3.Здесь выполнили действие умножения.

Закрепление:

1)Замена нескольких сумм произведением, при этом дети устанавливают, что означает каждое число в новой записи.

2)Замена произведения суммой и выполнение сложения.

2 * 7 = 2 + 2 + 2 + 2 + 2 + 2 + 2

3)Зарисовка примеров на умножение и сложение одинаковым слагаемым.

4)По рисункам записать примеры и решить.

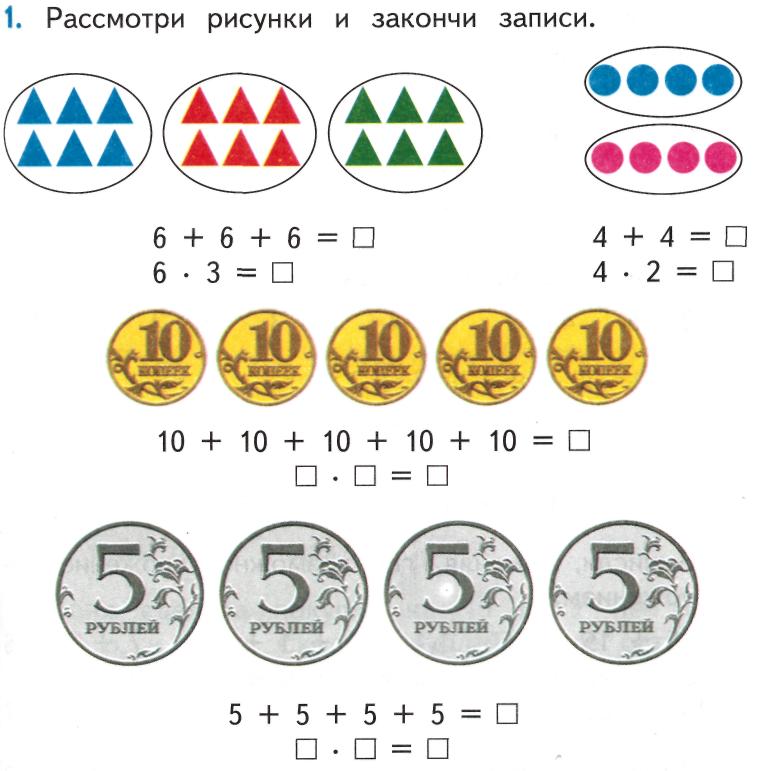
5)4 * 6 4 + 6. Сравнить примеры и решить их.

6)Сравнить выражения 18 * 2… 18 * 3 3 * 4…2 * 4

4 + 4 + 4…4 * 2 4 * 7 + 4…4 * 9

7)Решить второй пример, пользуясь первым:

2 * 7 = 14 2 * 10 = 20

2 * 8 = 2 * 11 =

8)Найди ошибку и исправь:

81 + 81 = 81 * 2

44 + 44 + 44 + 44 = 44 + 4

17 + 17 – 17 – 17 – 17 = 17 * 5

21 * 3 = 21 + 22 + 23

2.Смысл действия деления.

Раскрывается смысл действия деления в процессе решения простых задач на деление по содержанию и на равные части. Учащиеся должны научиться выполнять по условию задачи операцию разбиения данного множества на ряд равночисленных подмножеств и связать эту операцию с действием деления.

Основной метод работы: практический. Выполнение практических действий с предметами или зарисовка в тетрадях.

Сначала рассматриваем задачи на деление по содержанию.

Например: 8 апельсинов разложили в вазы по 4 на каждой. Сколько ваз потребуется?

А затем на деление на равные части:

Например: 8 апельсинов разложили на 4 вазы поровну. Сколько апельсин на 1 вазе?

Для закрепления смысла действия деления решаются задачи обоих видов с опорой на предметные действия и наглядности. В это же время дети знакомятся с названиями компонентов действия деления и умножения.

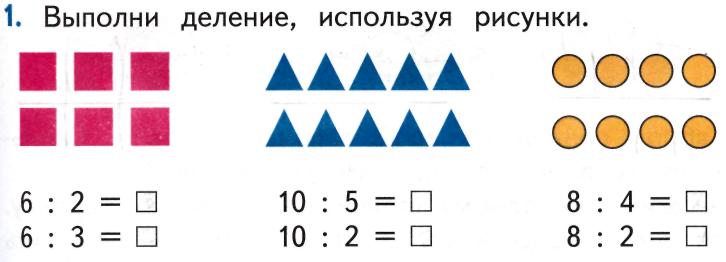
1. Умножение и деление в пределах 100.

3. 1. Табличное умножение и деление

Одной из основных тем программы по математике для II класса является умножение и деление в пределах 100. Эта тема включает ряд вопросов теории, на основе которой изучается табличное умножение и деление, внетабличное умножение и деление, деление с остатком и особые случаи умножения и деления (с единицей и нулем).

К табличному умножению относятся случаи умножения однозначных натуральных чисел на однозначные натуральные числа, результаты которых находят на основе конкретного смысла действия умножения. Соответствующие этим примерам случаи деления тоже называют табличными.

К внетабличному умножению относят умножение и деление в пределах 100: двузначные числа на однозначные, умножение однозначных на двузначные, а также деление двузначных на двузначные, деление с остатком.

К особым случаям относят умножение и деление с числом 0, а также умножение и деление на 1.

Табличное умножение и деление изучается совместно, т.е. из каждого случая умножения получают соответствующие случаи деления.

Основа знания учащимися связи между компонентами и результатом действий. Табличные случаи умножения и деления с каждым числом изучаются примерно по одному плану.

1.Составляется таблица с первым постоянным множеством.

2.Составляется таблица со II постоянным множителем (или наоборот).

Составление таблиц ведется вместе с детьми. В первом случае

3 * 3 – 3 * 2 + 3 3 + 3 + 3

3 * 4 = 3 * 3 + 3 3 + 3 + 3 + 3

Обязательно! Связь второго множителя и значения произведения. На сколько каждый увеличивается.

Во II случае нет связи с предыдущим примером, но легче детям запомнить.

После составления первого столбика таблицы, начинающегося с одинаковых множителей, дети самостоятельно составляют второй столбик опираясь на переместительный закон умножения.

Далее дети составляют 2 столбика примеров с соответствующими случаями деления, опираясь на умножение. После чего проводится работа по заучиванию таблиц умножения и деления наизусть.

Таблица умножения двух

Осознание смысла действия умножения позволяет учащимся самостоятельно составить первую таблицу умножения двух.

Проблема в том, чтобы заполнить таблицу, довести ёе знание до автоматизма. В действующем учебнике математики это решается увеличением времени на усвоение первой составленной таблицы. Здесь необходимо помнить о сокращении порции для заучивания. Таблицу лучше разбить на «порции» и по 2-3 или 3-4 примера.

Как составлять таблицу? В истории методики формирования навыков табличного умножения имеют место различные подходы к решению этой задачи.

Так, действующая сейчас методика рекомендует составлять сначала таблицу по первому постоянному множителю: 2 * 2; 2 * 3; 2 * 4. В этом случае они осознают взаимосвязь примеров, записанных в таблице, и смысл самого действия умножения.

Но возможно начать работу и с составления таблицы по постоянному II множителю 2 * 2, 3 * 2, 4 * 2…В этом случае прием замены произведения суммой содержит меньшее число операций и навыки формируются быстрее. Усвоение таких случаев связано с формированием умения, которое затем переходит в навык применять переместительное свойство умножения.

Приемы запоминания таблицы умножения

1. счет двойками, тройками, пятерками;

2. последовательного сложения;

3. прибавления слагаемого к предыдущему результату (вычитание из предыдущего результата);

4. взаимосвязанной пары: 2*6 6*2 (перестановка множителей);

5. запоминания последовательности случаев с ориентиром на возрастание второго множителя;

6. «порции»;

7. запоминание случая в качестве опорного;

8. внешней опоры;

9. запоминание таблицы с конца;

10. пальцевый счет при запоминании таблицы умножения;

мнемонические приемы при заучивании таблицы умножения.

Приемы запоминания таблицы деления.

1. прием, связанный со смыслом деления;

2. прием, связанный с правилом взаимосвязи компонентов умножения и деления.

Работа по развитию математической речи:

-5 умножить на 3 равно 15 -15 разделить на 3 равно 5

-произведение чисел 5 и 3 равно 15 -частное чисел 15 и 3 равно 5

-I множитель 5; второй множитель -делимое 15 делитель 3,

3, произведение 15 частное 5

-трижды 5 _ 15 -15 уменьшаем в 3 раза = 15

-5 увеличиваем в 3 раза = 15

Упражнения:

-составление таблицы Пифагора

-повторение таблицы по порядку и вразбивку (мяч)

-карточки с примерами 7 * 8 обратная сторона (56)

-математическое домино

-отгадывание задуманного числа

-составление примеров на умножение и деление с тройками чисел 3, 7, 21; 86, 48.

3.2. Внетабличное умножение

Случаи внетабличного умножения и деления изучаются в следующем порядке:

1. Умножение и деление чисел, оканчивающихся нулем.

2. Умножение двузначного числа на однозначное число и однозначного числа на двузначное.

3. Деление двузначного числа на однозначное число.

4. Деление двузначного числа на двузначное.

5. Проверка умножения и деления.

Умножение и деление чисел, оканчивающихся нулем

Решение таких примеров сводится к умножению и делению однозначных чисел, выражающих число десятков.

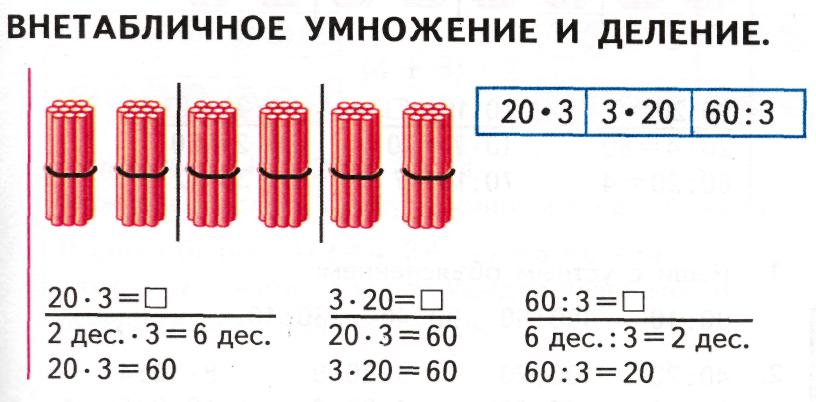
При умножении однозначного числа на двузначное используем переместительный закон умножения 4*20=20*4=80.

Деление двузначного числа (80) на двузначное (20) выполняется способом подбора частного на основе связи между компонентами деления.

80:20 – необходимо найти такое число, чтобы 20*х=80, подбираем 20*3=60 (мало), 20*4=80 (подходит), следовательно 80:20=4.

Умножение двузначного числа на однозначное.

Эта тема не требует особых объяснений.

Подготовка:

-вычисление выражений вида (10+4)*3; (10+2)*8

-название компонентов сложения и умножения.

Знакомство:

Дети могут самостоятельно ознакомиться с этим приемом, опираясь на свойство а*(в+с) или работая по развернутой записи

12*3=(10+2)*3=10*3+2*3=30+6=36

Для слабых работа с наборным полотном и палочками.

23*4 – по 23 палочки взяли 4 раза.

Ученик берет 2 пучка и 3 отдельные палочки, повторяет это движение 4 раза. Вкладывает в наборное полотно.

20*4 3*4

80 + 12

Также при ознакомлении учащихся с этим приемом можно использовать опорную схему.

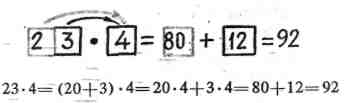
Алгоритм:

1.Умножаю десятки.

2.Умножаю единицы.

3.Складываю.

4.Читаю ответ.

Закрепление:

-сопоставление примеров вида 6*12; 12*6

-сравнение приемов умножения и деления 3*14=3*(10+4)=3*10+3*4=42

30+14=30*(10+4)=30+10+4=44

-работа с окошечками….

Деление двузначного числа на однозначное

Используется свойство (а+в)*с

Этот случай внетабличного деления усваивается детьми труднее, чем умножение двузначного на однозначное. При таком виде деления встречаются разные группы примеров:

Уделить внимание разбору каждого вида примеров, указать на какие слагаемые заменяем делимое: в первом примере на разрядные, во всех остальных на удобные.

Подготовка:

-выделить круглые числа, делимые на 2, 3, 4 и т.д.

-представить разными способами числа в виде суммы 2 слагаемых, каждое из которых делится на число без остатка;

-решить пример разными способами (18+45):9

После подготовительной работы сначала рассматриваем примеры 1, 2 группы – они являются для детей легкими. Можно рассмотреть их на примере умножения двузначного числа на однозначное число.

Затем изучаем примеры 3 группы. Здесь детям предлагается самим решить пример при этом делимое заменить суммой слагаемых.

42:3 42:3=(30+12):3=30:3+12:3=10+4=14

42:3=(27+15):3=

42:3=(24+28):3=

Вывод:

Удобен первый способ, т.к. при делении удобных слагаемых получаем разрядные слагаемые частного.

Наиболее трудными примерами для детей считаются примеры 4 и 5 группы. Дети должны прийти к выводу, что делимое заменяем суммой удобных слагаемых, при этом первым удобным слагаемым надо выделять число, которое выражает наибольшее число десятков делимого на делитель; вычтя это число из делимого, найдем второе удобное слагаемое.

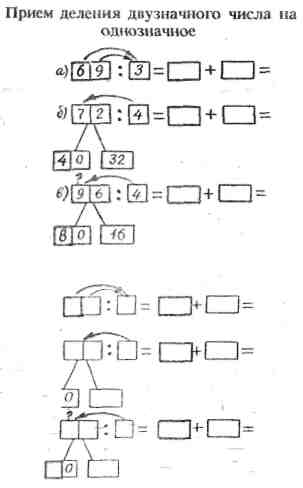
Опоры: прием деления двузначного числа на однозначное.

Деление двузначного числа на двузначное.

В этом случае при делении двузначного на двузначное используем способ подбора частного, который основан на связи между компонентами:

Можно предложить детям другой способ решения:

91:13

1.Смотрим на единицы (1 и 3)

2.Определяем, можно ли разделить 1 на 3

3.Подбираем двузначное число, заканчивающееся на 1 и делим на 3; 21:3=7

4.Пробуем 91:13=7

5.Проверяем: 13*7=(10+3)*7=70+21=91

Опора: Прием деления двузначного числа на двузначное число:

68 : 17=4 …. : ….=….

Проверка умножения и деления.

Дети достаточно хорошо знают, что умножение и деление – это взаимообразные действия. Здесь необходимо показать, что знание связи между умножением и делением могут быть использованы для проверки правильности выполнения вычислений.

Но: дети действуют механически:

85:5=5=:5+35:5=10+9=19 19*5=85

Надо учить детей тому, как найти возможный ответ, внимательно рассмотрев делимое и делитель. Необходимо обратиться ко второму способу «прикидке».

Например: 95:19 – нужно вспомнить табличные случаи

48:24 – сравнить единицы обоих чисел =”2”

87:29 – вспомнить когда Х*9=….7 – табличное значение.

Умножение проверяем действием деления.

Приемы для закрепления внетабличных случаев.

1.Противопоставление (выявляются существенные признаки различия в способах нахождения результатов): 23*4 и 23+4; 46:2 и 46+-2; 66:2 и 66:22.

2.Сопоставление (выделяются существенные признаки сходства):

46*2 и 46:2

Данные приемы облегчают усвоение детьми каждого нового алгоритма на основе уже хорошо знакомого, а фиксирование внимания на признаках различия предупреждает необоснованно широкий перенос имеющихся знаний на новые случаи.

3.Вооружение учеников знанием различных способов самопроверки и воспитание привычки к самоконтролю.

4.Дополнительная (в том числе и опережающая) работа с теми учениками, которые допускают (или могут допускать) ошибки в вычислениях.

Как свидетельствует наш опыт, эффективными являются также следующие методические приемы:

• Использование система опорных схем.

• Организация практических работ по выполнению заданных действий над материализованными образами двузначных чисел – пучками палочек и отдельными палочками.