Просмотр содержимого документа
«Уравнения Бернулли»
Тема: Уравнение Бернулли
Теоретическая часть
Уравнение вида
y’ + p(x)y = q(x)yn, (*)
где n≠0 и n≠1 называется уравнением Бернулли.
Разделим обе части уравнения y’ + p(x)y = q(x)yn на yn, получим:
y-ny’ + p(x)y-n+1 = q(x) (**).
Обозначим: y-n+1 = z. Тогда z’ = (-n + 1)y-ny’. Отсюда находим y-ny’ = 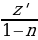 . Уравнение (**) примет вид:
. Уравнение (**) примет вид:
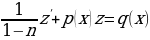 .
.
Последнее уравнение является линейным относительно z, решение его известно.
Пример 1: Найти решение задачи Коши
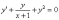 ,
, 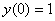
Данное дифференциальное уравнение является уравнением Бернулли, разделим обе части на y2 :
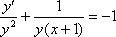
Проведем замену:
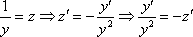
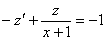
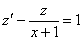
Получено линейное неоднородное уравнение, решением которого является функция
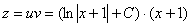
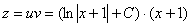
Обратная замена:
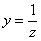
Общее решение:
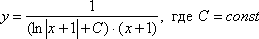
Найдем частное решение, соответствующее заданному начальному условию:
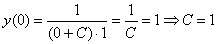
Таким образом, частное решение данного уравнения имеет вид:

Пример 2: Найти решение дифференциального уравнения, удовлетворяющее начальному условию :
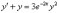 ,
, 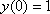
Решение: Данное ДУ является уравнением Бернулли. Найдем общее решение.
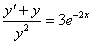
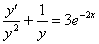
Проведем замену:
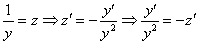
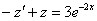
Получено линейное неоднородное уравнение, решение которого является функция
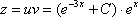
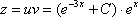
Обратная замена:
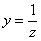
Общее решение:
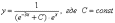
Найдем частное решение, соответствующее заданному начальному условию:
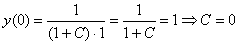
Таким образом, частное решение данного уравнения имеет вид:
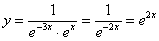
Задачи для самостоятельного решения
1. y’ + y = xy2
2. y’ – y = xy2
3. y’ + 2y = xy3
4. y’ – 2y = xy3
5. y’ + y = x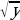
6. y’ – y = - x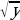
7. y’ + y = x2y2
8. y’ – y = x2y2
9. y’ + 2y = x2y2
10. y’ - 2y = x2y2
11. y’ + y = 2xy3
12. y’ - y = 2xy3
13. y’ + 2y = 2xy2
14. y’ - 2y = 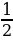 xy2
xy2
15. y’ - 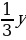 = xy2
= xy2
16. y’ - 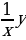 = y2
= y2
17. y’ + 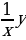 = y2
= y2
18. y’ - 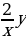 = y2
= y2
19. y’ + 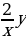 = y2
= y2
20. y’ - 3y = xy3
21. y’ + 3y = xy2
22. y’ + 3y = 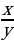
23. y’ + 2y = y2ex
24. y’ – 2y = y2e-x
25. y’ + 2y = y2e-2x
Дополнительные задания
1. 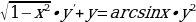 , y(0) = -1
, y(0) = -1
2. y’ + y = 3e-2x y2, y(0) = 1
3. 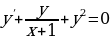 , y(0) = 1
, y(0) = 1
4. y’ + y·ctgx = y4sinx, 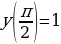
5. 2y’ – 3y·cosx = -e-2x(2 + 3cosx)y-1, y(0) = 1





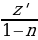 . Уравнение (**) примет вид:
. Уравнение (**) примет вид: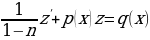 .
.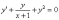 ,
, 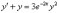 ,
, 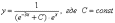
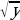
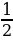 xy2
xy2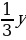 = xy2
= xy2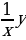 = y2
= y2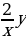 = y2
= y2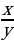
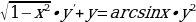 , y(0) = -1
, y(0) = -1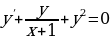 , y(0) = 1
, y(0) = 1