Дата
Тема урока: УРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЯМИ
Цели: закрепить умения решать различные уравнения и неравенства, содержащие модуль.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Подготовка к ЕГЭ. Выполните устно предложенные задания.
Решите неравенство:
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Откройте тетради и запишите сегодняшнее число и тему урока. Начинаем подготавливаться к контрольной работе. Сегодня повторим, как решать уравнения и неравенства с модулем.
№1. Решить уравнение 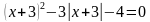 .
.
Выполним замену:
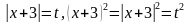 .
.
Получим и решим квадратное уравнение:
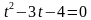 ,
,
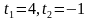 .
.
Тогда исходное уравнение будет эквивалентно совокупности уравнений:
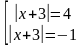
Второе уравнение совокупности решений не имеет, т.к. 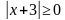 . Решаем первое по свойству модуля:
. Решаем первое по свойству модуля:
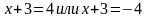
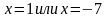 .
.
Ответ: 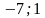 .
.
№2. Решить иррациональное уравнение 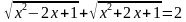 .
.
Заметим, что под знаками корня находятся выражения, которые можно свернуть по формулам сокращенного выражения:
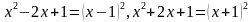 .
.
Тогда перепишем исходное уравнение в виде:
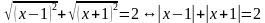 .
.
Приравняем подмодульные выражения к нулю, получим х1=1 и х2= -1. Эти точки разбивают всю числовую прямую на три интервала:
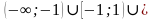 .
.
-
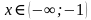 . Нужно узнать, с какими знаками (+ или - ) раскроются модули. Выполнив подстановку любого числа из интервала, получим:
. Нужно узнать, с какими знаками (+ или - ) раскроются модули. Выполнив подстановку любого числа из интервала, получим:
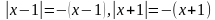 .
.
Тогда получим уравнение:
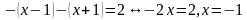
Но 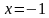 не принадлежит
не принадлежит  , а значит, не является корнем исходного уравнения.
, а значит, не является корнем исходного уравнения.
-
 . На этом интервале модули раскроются следующим образом:
. На этом интервале модули раскроются следующим образом:
 .
.
Получим уравнение:
.
-
 . Проверим как раскроются модули на этом интервале:
. Проверим как раскроются модули на этом интервале:
 .
.
Получим уравнение:
.
Теперь необходимо объединить между собой решения на каждом из трех этапов, при этом на первом решений не было, только на втором и третьем. Получим:
 .
.
Ответ:  .
.
№3. Решить уравнение .
Рассмотрим знаменатель, он не должен быть равен нулю. Перепишем его с помощью формулы сокращенного умножения в виде  . Это наше ОДЗ.
. Это наше ОДЗ.
Преобразуем уравнение  и сократим на скобку (х-3), получим:
и сократим на скобку (х-3), получим:

Распишем его по свойству модуля в виде совокупности двух уравнений

Раскроем как пропорцию, получим:
Оба этих корня удовлетворяют ОДЗ, значит оба идут в ответ.
Ответ: 2; 4.
№4. Решить неравенство  .
.
Распишем его как двойное неравенство с помощью равносильности:
 .
.
Решить двойное неравенство – значит найти решение соответствующей ей системе неравенств. Она выглядит следующим образом:
Решим первое неравенство  .
.
Решим это неравенство методом интервалов:
Решением первого неравенства является .
Решим теперь второе неравенство  .
.
Решим это неравенство методом интервалов:
Решением второго неравенства является  .
.
Но это решения каждого из неравенств отдельно, а у нас по условию система. Следовательно, на общую координатную прямую необходимо нанести решения каждого из них и найти пересечение полученных множеств:
Ответ: .
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание: подготовиться к с/р.
№1. Решить неравенство  .
.
№2. Решить уравнение  .
.







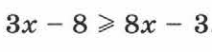
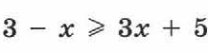
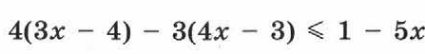
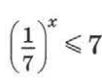
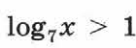
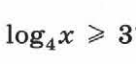
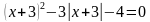 .
.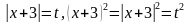 .
.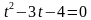 ,
,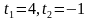 .
.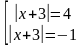
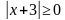 . Решаем первое по свойству модуля:
. Решаем первое по свойству модуля: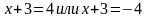
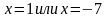 .
.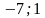 .
.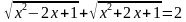 .
.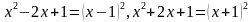 .
.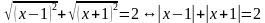 .
.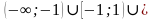 .
.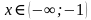 . Нужно узнать, с какими знаками (+ или - ) раскроются модули. Выполнив подстановку любого числа из интервала, получим:
. Нужно узнать, с какими знаками (+ или - ) раскроются модули. Выполнив подстановку любого числа из интервала, получим: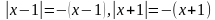 .
.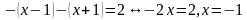
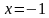 не принадлежит
не принадлежит 


















