Уравнения и системы уравнений.
Иррациональные уравнения
Уравнение, содержащее неизвестную под знаком корня n-ой степени, называется иррациональным.
Иррациональное уравнение чаще всего решается путём возведения в степень, которую имеет корень, содержащий неизвестную, или заменой неизвестной. Не следует забывать, что в степень возводятся обе части уравнения.
При возведении в нечётную степень обеих частей уравнения, получаем уравнение, равносильное исходному.
Новое уравнение, получившееся после возведения в чётную степень обеих частей, не всегда равносильно исходному уравнению, поэтому необходимо либо выполнить проверку полученных значений неизвестного путём подстановки в исходное уравнение, либо отбросить корни, не принадлежащие области определения уравнения.
Пример 15. Решить уравнение 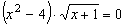 .
.
Решение:
Область определения: х + 1 ≥ 0.
x2 – 4 = 0 или х + 1 = 0;
х1 = – 2 , х3 = – 1.
х2 = 2,
х1 = – 2 не принадлежит области определения.
Ответ: – 1; 2
Пример 16. Решить уравнение .
Решение:
Данное уравнение решается возведением в квадрат левой и правой частей, и, так как в правой части уравнения содержится переменная, мы получим уравнение не равносильное исходному.
15 – 3х = х2 + 2х + 1; х2 + 5х – 14 = 0; х1 = – 7, х2 = 2.
Проверка. При х1 = – 7, 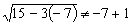 – не корень.
– не корень.
При х2 = 2, 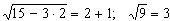 – корень.
– корень.
Ответ: 3.
Пример 17. Решить систему

Решение:

Замечание. В данном случае не требуется ни проверка, ни нахождение области определения, поскольку правые части обоих уравнений и до возведений в квадрат, и после – заведомо положительны.
Ответ: (29; 20).
Уравнения, содержащие знак модуля
Пример 18. Решите уравнение 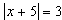 .
.
Решение:
х + 5 = 3 или х + 5 = – 3. Откуда х1 = – 2 или х2 = – 8.
Ответ: – 2; – 8.
Пример 19. Решите уравнение 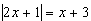 .
.
Решение:
Данное уравнение будем рассматривать на двух числовых промежутках: .
.
Значение –1/2 назовём пограничным, т.е. при х = –1/2, 2х – 1 = 0.
При 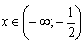 имеем –(2x+1)=x+3; -3=4; x=-4/3 - число принадлежит рассматриваемому промежутку, следовательно, –4/3 - корень.
имеем –(2x+1)=x+3; -3=4; x=-4/3 - число принадлежит рассматриваемому промежутку, следовательно, –4/3 - корень.
При 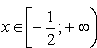 имеем 2x+1=x+3; x=2 – принадлежит рассматриваемому промежутку, следовательно, является корнем.
имеем 2x+1=x+3; x=2 – принадлежит рассматриваемому промежутку, следовательно, является корнем.
Помните! Пограничное значение смены знака необходимо включить хотя бы в один из интервалов.
Ответ: -4/3; 2.
Пример 20. Решите уравнение 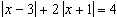 .
.
Решение:
Двучлен х – 3 меняет свой знак при переходе через х = 3, а х + 1 – при х = – 1. Данное уравнение будем рассматривать на трёх числовых промежутках: 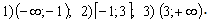
1)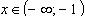 ; имеем-(x-3)-2(x+1)=4; – 3х = 3; х = – 1.
; имеем-(x-3)-2(x+1)=4; – 3х = 3; х = – 1.
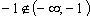 и не является корнем.
и не является корнем.
2) 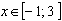 ;-(x-3)-2(x+1)=4; х = – 1.
;-(x-3)-2(x+1)=4; х = – 1.
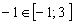 , – 1 – корень.
, – 1 – корень.
3) 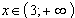 ;(x-3)-2(x+1)=4; 3х = 5; х =5/3.
;(x-3)-2(x+1)=4; 3х = 5; х =5/3.
 , следовательно, корнем не является.
, следовательно, корнем не является.
Ответ: – 1.
Пример 21. Решить систему

Решение:
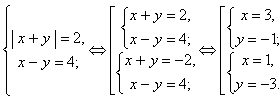
Ответ: (3; – 1), (1; – 3).
Уравнения с параметром
Пример 22. При каком значении а уравнение х(2 – а) – х = 5 + х не имеет решений?
Решение:
Выразим х через а. 2х – ах – х – х = 5; – ах = 5; х = –5/a .
При а = 0 х не определён.
Подставим а = 0 в исходное уравнение: х(2 – 0) – х = 5 + х; 2х – 2х = 5; 0 ≠ 5, следовательно, при а =0 данное уравнение не имеет решения.
Ответ: при а = 0.
Пример 23. Корни х1 и х2 уравнения х2 + х + а = 0 обладают свойством x12+x22=5 . Найти а.
Решение:
Уравнение х2 + х + а = 0 – приведённое квадратное. По теореме Виета х1 + х2 = – 1, х1 ∙ х2 = а. Т.к. x12+x22=5, то х1 – х2 = – 5.
Имеем х1 = – 3; х2 = 2, следовательно, а = (– 3)∙2= – 6.
Ответ: а = – 6.
Пример 24. При каких значениях параметра n уравнение (n-2)x2-2nx+n+3=0 имеет корни разных знаков.
Решение:
n – 2 ≠ 0. В противном случае – нет квадратного уравнения.
Приведём исходное уравнение (путём почленного деления обеих частей равенства на n – 2) к приведённому:

Чтобы уравнение имело корни разных знаков, необходимо и достаточно выполнение двух условий одновременно:
1) D/4 0 (по формуле чётного коэффициента);
2) x1 ∙ x2 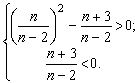

Ответ: 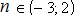 .
.
Решите самостоятельно
1) Решите уравнение 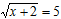 .
.
2) Решите уравнение 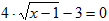 .
.
3) Решите уравнение 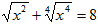 .
.
4) Решите уравнение 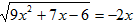 .
.
5) Решите систему уравнений 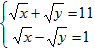 .
.
6) Решите систему уравнений 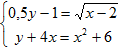 .
.
7) Пусть (х0; у0) решение системы уравнений 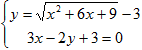 . Найдите произведение х0 ∙ у0.
. Найдите произведение х0 ∙ у0.
8) Решите систему уравнений 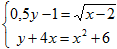 .
.







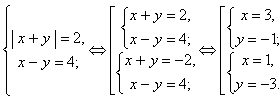
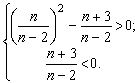

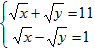 .
.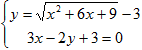 . Найдите произведение х0 ∙ у0.
. Найдите произведение х0 ∙ у0.









