| 1.Организационный этап
2. Актуализация знаний учащихся
Разбор задачи на применение алгоритма решения задач.
Этап закрепления изученного материала.
| 1.Организационный момент, настрой на урок Создание благоприятной психологической среды: Приветствие.
2. Актуализация знаний учащихся. Ответить на вопросы: 1.Определить знак первого коэффициента. 2.Определить знак дискриминанта. 3.Какое значение наибольшее или наименьшее существует? 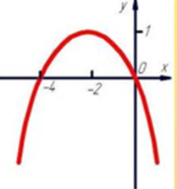 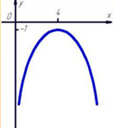 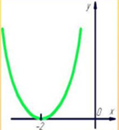 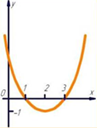
| Ф. И. класс | | 
Настроение в начале урока 
Настроение в конце урока | | № | Вид задания | Максимальный балл | Полученный балл | |
| Математический диктант | 8-«5» 6-7 -«4» 4-5-«3» б- “2” |
| | 1 | Задача №1 | 2 балла |
| | 2 | Задача №2 | 2 балла |
| | 4 | Задача №3 | 4балла |
| |
| Задача №4 | 2 балла |
| | Оценка за урок: |
| | Оцени свою работу на уроке: |
Математический диктант «да-нет» Цель: концентрация внимания учащихся Верно «+», неверно «-». 1.Функция у=-6+4х2 -5х является квадратичной 2.Графиком этой функции является прямая 3.Областью определения функции является множество всех действительных чисел 4.Эта функция имеет наибольшее значение 5.График функции симметричен относительно начала координат 6.Если телу сообщить начальную скорость, направленную под углом к горизонту, то траектория движения этого тела будет иметь такой же вид, как график квадратичной функции 7.Правда ли, что графиком зависимости кинетической энергии тела от его скорости является парабола? 8.Правда ли, что графиком зависимости потенциальной энергии тела от его высоты является парабола? Самопроверка ( + - + - + + + - ) Самооценка: В каких заданиях у вас возникали затруднения? Почему? 3. Сообщение темы, постановка целей урока.
Сегодня на уроке мы продолжим работать с квадратичными функциями, будем использовать квадратичную функцию для решения прикладных задач. Парная работа: По карточкам. Задание 1 : Задача Мяч подброшен вертикально вверх. Зависимость высоты мяча над землей h (м) от времени полета t (с) выражается формулой h = – 5t2 + 10t + 1,5. На какую максимальную высоту поднимется мяч? Решение.  Траектория полёта представляет собой параболу, ветви которой направлены вниз, своего наибольшего значения она достигнет в вершине параболы, т. е. решение задачи свелось к нахождению координат вершины параболы: t 0= 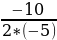 =1, h = – 5* =1, h = – 5*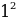 + 10*1 + 1,5 = 6,5 (м). + 10*1 + 1,5 = 6,5 (м). О т в е т: 6,5 метра. Дескриптор: Обучающийся - находит значение аргумента, при котором функция достигает максимального значения;
Парная работа Задача 1 Зависимость высоты прыжка спортсмена над землей h (м) от времени полета t (с) выражается формулой h = – 3 t 2 + 6 t +2. На какую максимальную высоту поднимется спортсмен в прыжке с шестом ? Постройте график данной функции .

t 0= 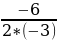 =1, =1, h = – 3*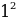 + 6*1 + 2 = 5 (м). + 6*1 + 2 = 5 (м). О т в е т: 5 метров.
Дескриптор: Обучающийся - строит график функции; - находит значение аргумента, при котором функция достигает максимального значения;

Задача 2. Некоторые процессы, происходящие вокруг нас, можно описать с помощью квадратичной функции. Если эту функцию задать с формулой или графически, то легко найти ответы на разнообразные вопросы. В следующих задачах вы рассмотрите несколько примеров применения квадратичной функции. Работа в парах: 1. Здание Национального архива Республики Казахстан построено в Астане в 2003 году. Хранилище архива имеет куполообразную форму, ограниченную параболой 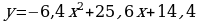 . Определите высоту хранилища. . Определите высоту хранилища. Решение. Для определения высоты здания найдем значение функции в вершине параболы: 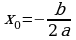 , , 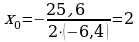 , тогда , тогда 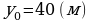 . . Таким образом, высота хранилища 40 метров. Ответ: 40 м.
Обучающийся - строит график функции; -определяют высоту здания.
Задача №3 (Парная работа) Исследование, проведенные в одной крупной производственной компании, показали, что производительность труда в течение рабочего времени меняется в зависимости от времени работы по закону N(t) = - 0,2t 2 +1,6t +3. Используя график функции, считая, что рабочий день равен 8 ч и ответьте на вопросы: 1) В какой промежуток времени растет производительность труда? 2) В какое время производительность труда достигает максимума? 3) Промежуток рабочего дня, во время которого производительность труда падает? 4) Сравните производительность труда через 2 часа и через 6 часов после начала работы. В какое время производительность выше? t 0= 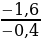 =4 h = -0,2* =4 h = -0,2*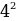 + 1,6*4 +3 = 6,2 + 1,6*4 +3 = 6,2 | t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | | N | 3 | 4,4 | 5,4 | 6 | 6,2 | 6 | 5,4 | 4,4 | 3 | Ответ: 1. [0;4] 2. 4ч 3. [4;8] 4. 5,4=5,4; Дескриптор: Обучающийся - строит график функции; - находит промежутки возрастания функции; - определяет по графику максимальное значение функции; - находит значение аргумента, при котором функция достигает максимального значения; - находит производительность труда по заданным значениям времени; - сравнивает найденные значения и делает вывод.
|
Отвечают на вопросы (самопроверка)
Таким образом, учащиеся разбиваются на пары, в которых будут работать в процессе урока.
Работают в паре и у доски.
Работают на рабочих листах.
Работают на рабочих листах
Учащиеся работают на рабочих листах, отвечают на вопросы. |
Наблюдение учителя за ответами учащихся. Похвала учителя
наблюдение за работой учащихся, оказывая консультации
наблюдение за работой учащихся, оказывая консультации
ФО
наблюдение за работой учащихся, оказывая консультации
ФО
наблюдение за работой учащихся, оказывая консультации ФО
наблюдение за работой учащихся, оказывая консультации ФО Выставление баллов в оценочном листе.
|
Слайд №4
Слайд №5
Приложение 1
Слайд №7
Слайд №2,3
Слайд №8 Слайд №9
Слайд № 10 Слайд № 11
Слайд №12 Слайд№13
Слайд№14 №15
|
| Этап самостоятельной работы ФО
| Задача 4. На полигоне, с высоты в два метра, под углом к горизонту была выпущена сигнальная ракета. Изменение высоты её полёта h (метры) в зависимости от времени движения t (секунды) описывается формулой h = 2 + 20t − 5t2 . Постройте график зависимости высоты поднятия ракеты от времени и ответьте на вопросы: 1) В какое время ракета поднимется на высоту 17 м? В какое время она окажется на той же высоте при спуске? 2) На какой высоте будет находиться ракета через 3,5 с полёта? 3) Укажите наибольшую высоту подъёма ракеты. 4) Сколько времени потребовалось ракете, чтобы подняться на максимальную высоту? t 0= 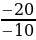 =2 h = -5* =2 h = -5*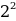 + 20*2 +2 = 22 + 20*2 +2 = 22 | t | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | | N | 2 | 10,75 | 17 | 20,75 | 22 | 20,75 | 17 | 10,75 | 2 | Ответ: 1. 1с; 3с 2. 10,75м 3. 22м 4. 2с
Дескриптор: Обучающийся - строит график функции - находит значение функции; - находит значение аргумента; - определяет по графику наибольшее значение функции; - находит при каком значении аргумента функция достигает своего наибольшего значения.
| Работают в рабочих листах
Выполняют самостоятельную работу | Наблюдение за работой учащихся, оказывая консультации ФО
| Слайд №15 Приложение 4
Слайд №16,17
Слайд №17
|













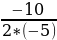 =1, h = – 5*
=1, h = – 5*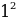 + 10*1 + 1,5 = 6,5 (м).
+ 10*1 + 1,5 = 6,5 (м). 
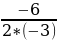 =1,
=1, 
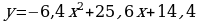 . Определите высоту хранилища.
. Определите высоту хранилища.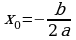 ,
, 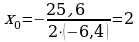 , тогда
, тогда 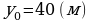 .
.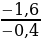 =4 h = -0,2*
=4 h = -0,2*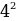 + 1,6*4 +3 = 6,2
+ 1,6*4 +3 = 6,2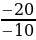 =2 h = -5*
=2 h = -5*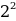 + 20*2 +2 = 22
+ 20*2 +2 = 22









