Урок алгебры в 11 классе "Показательная функция, ее свойства и график"

этап

деятельность

Показатель выполнения задач

учитель

ученики

I Оргмомент

Задача: проверить готовность

Приветствует учащихся, визуально определяет готовность класса к уроку.

Приветствуют учителя, садятся.

Кратковременность момента организации.

II Целеполагание

Задача: соотнести имеющиеся знания с новыми понятиями

Учитель создает проблемную ситуацию с помощью вопросов:

1. Какая функция называется степенной? Привести примеры.

2. Какие свойства функции вы знаете?

3. Какие преобразования графика функции вы знаете?

4. (2 слайд) Поставьте в соответствие графику функции формулу. Назвать все функции. Какие функции вам не знакомы? Чем они отличаются от остальных?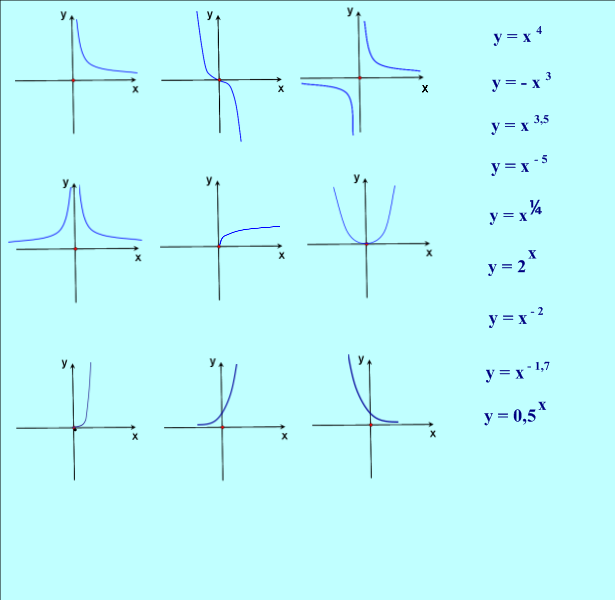

Отвечают на вопросы:

а) Степенной функцией называется функция вида

у = х^r, где r – любое действительное число. Например, у = х^0,5.

б) область определения, область значений, монотонность, четность/нечетность, ограниченность, непрерывность, выпуклость, экстремумы.

в) параллельный перенос вдоль оси Ох и Оу, растяжение/сжатие вдоль оси Ох и Оу, симметрия относительно оси Ох и Оу.

г) (один ученик выходит к доске и с помощью перетаскивания соотносит формулу с графиком, остальные проверяют и, при необходимости, помогают) Все функции являются степенными, кроме двух: у = 2^х и

у = 0,5^х. Здесь переменная находится не в основании, а в показателе степени.

Выделены из перечня неизвестные функции, отмечены отличия их от остальных функций.

III Изучение нового материала.

Задача: расширить знания о функциях на примере показательной функции

Давайте построим график функции у = 2^х по точкам. Что для этого необходимо сделать? На прошлых уроках мы говорили, что степень с основанием 2 существует при любом показателе степени, значит, при построении графика функции мы можем соединять точки на координатной плоскости сплошной линией (таблицу заполнить на 3 слайде, отметить точки на координатной плоскости и кликнуть в области координатной плоскости, чтобы появился график).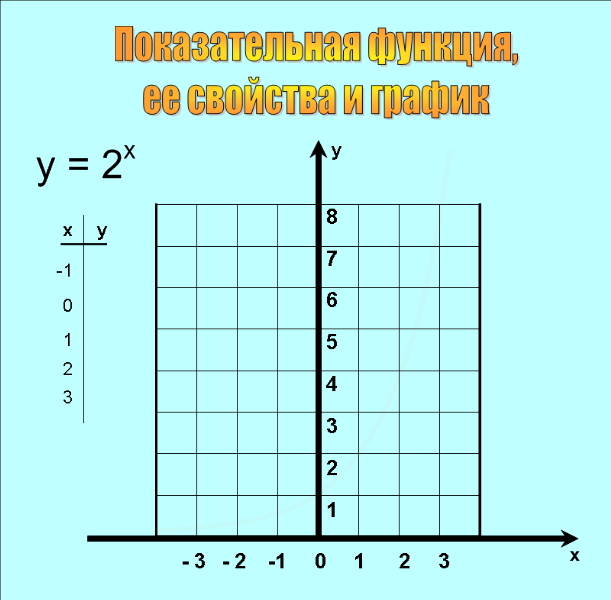

Аналогично построим график функции у = 0,5^х (4 слайд).

(5 слайд) Итак, функция у = а^х, где а0 и а  1 называется показательной, а ее график – экспонентой. Почему накладывается условие

а 0 и а  1? График любой функции у = а^х при а 1 имеет вид (на слайде слева), а график любой функции у = а^х при 0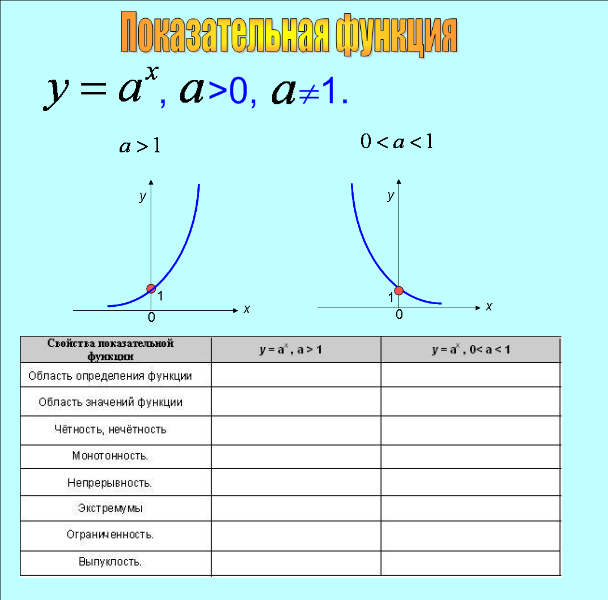

Дети отвечают на вопрос: построить таблицу значений.

Вместе с учителем дети в тетрадях заполняют таблицу значений и строят график функции.

Для построения графика второй функции к доске выходит один ученик, остальные - пишут в тетрадях.

Отвечают на вопрос: так как если показатель степени дробный, то по определению степени с дробным показателем, основание должно быть больше 0. А если а = 1, то функция будет иметь вид у = 1^х, графиком которой является прямая, параллельная оси Ох, т.е.график линейной функции.

Вместе с учителем учащиеся заполняют левую половину таблицы, а правую – самостоятельно.

Построены графики показательной функции при

а 1 и 0

IV Первичное закрепление.

Задача: установить осмысленность нового материала.

а) Какая из функций является показательной? Почему?

б) Какая из функций возрастает? Почему?

в) Найти множество значений функции

у = 2^х + 5.

Выбирают один из предложенных вариантов ответов, объясняя свой выбор

(ответ г)

(ответ в)

(ответ а)

По желанию один отвечает, остальные слушают и поправляют.

Верно выбранные варианты ответов, умение обосновать свой выбор.

Активность, внимание (через наблюдение).

V Совершенство-вание приобретенных умений.

Задача: проверить умение самостоятельно применять полученные знания при выполнении заданий.

Решить по учебнику №39.16 (аб) (проверка с помощью 7 слайда).

№39.29 (аб) и №39.30 (аб) (проверка с помощью 8 и 9 слайдов, графики перемещать в нужном направлении и по ним устно найти область значений).

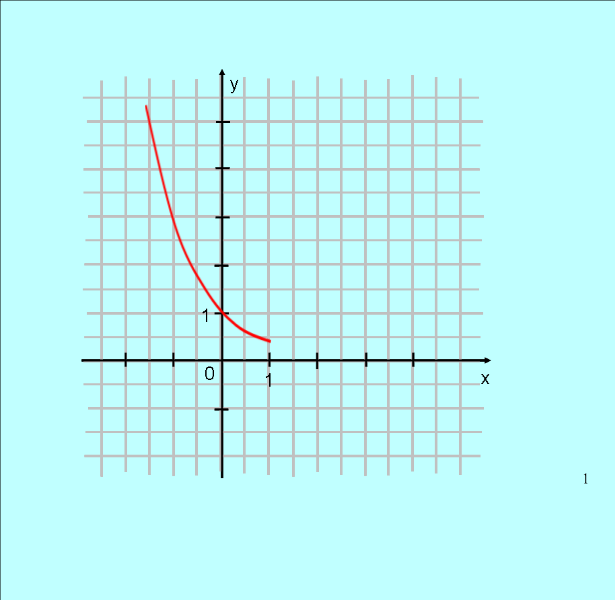
Самостоятельно выполняют задание на построение графиков показательной функции (с последующей проверкой по готовым чертежам на слайде).

Выполняют преобразование графиков функций. Один ученик показывает преобразования на интерактивной доске, остальные проверяют, корректируют.

Устно находят область значений функции с пояснениями.

Правильность построения графиков функций.

Умение слушать, аргументировать ответ.

VI Рефлексия.

Задача: определить уровень знания и незнания по данной теме

Вернемся к первому слайду (по гиперссылке) и проверим, все ли формулы показательных функций мы поставили верно к их графикам? Почему?

Итак, какая функция называется показательной? Привести примеры.

Анализируют свои первоначальные предполагаемые записи, делают выводы о правильности/неправильности выбора, корректируют записи.

Дают определение, приводят примеры.

Скорректированные записи на слайде.

VII Домашнее задание.

Задача: записать домашнее задание.

Записать в дневник задание:

на «3» - №39.16 (вг), 39.29 (вг)

на «4» - №39.31

на «5» - №39.33

Записывают задание в дневник, самостоятельно определяя объем задания.