План – конспект урока по алгебре в 7 Б классе ГБОУ СОШ № 47 г. Владикавказ по теме « Решение задач с помощью уравнений».
Учитель математики : Тадтаева Залина Зауровна.
Тип урока: урок обобщения и систематизации знаний, умений и навыков.
Методы обучения:
- объяснительно-иллюстративный;
- частично-поисковый;
- репродуктивный.
Формы организации познавательной деятельности:
- коллективная;
- индивидуальная.
Система контроля на уроке: сочетание контроля учителя, самоконтроля, самооценки.
Методы:
- на этапе актуализации: проблемный;
- на этапе отработки навыков: практический.
Цель: обобщить теоретические и практические знания, полученные на уроках математики.
Задачи:
Развивать умения использовать теоретические знания при решении задач.
Отрабатывать навык решения задач с помощью уравнений.
Развивать лингвистические умения учащихся: строить связное высказывание, давать логичный и последовательный ответ.
Развивать мыслительную деятельность учащихся. Развивать вычислительные навыки, память, самостоятельность, наблюдательность.
Оборудование: презентация,компьютер, экран, проектор, индивидуальные карточки,раздаточный материал.
Ход урока.
1. Оганизационный момент.
Учитель: Здравствуйте ребята! Сегодня у нас необычный урок, мы с гостями отправимся в необычное путешествие. На слайде записан эпиграф: « Числа правят миром».( слайд 2)
Этот тезис видвинул Пифагор. Чтобы начать наш урок с хорошим настроением,перед вами на столах лежат таблички со смайликами, покажите мне смайлик, выражающий ваше эмоциональное состояние. Повернитесь к друг другу с этими смайликами - улыбнитесь друг другу и мне.
Ученики: Поднимают таблички.
Учитель: Итак, начинаем. Запишите число в тетрадях, в которых вы выполняли домашнее задание и тему урока « Решение задач с помощью уравнений». А какие задачи мы будем решать,вы должны сами расшифровать по ребусу , приведенному на слайдах .( слайд 3- 5)
Ученики: Угадывают.
Учитель: Запишите тема урока : «Решение задач с помощью уравнений» и решать будем« Задачи Древней Греции».
Учитель: Сегодня мы с вами совершим погружение в мир древних греков.
Начало 1 периода зарождения математики неизвестно. О точном появлении математики мы можем судить по древним записям, в которых есть числа. Известно, что в 4-ом тысячелетии до нашей эры человек владел понятием величины и числа. В этом периоде особо следует выделить достижения математики Древнего Египта и Древнего Вавилона. Во всей математике Древнего Востока мы нигде не находим никакой попытки дать то, что мы называем доказательством. Мы имеем только предписания в виде правил: «делай то-то, делай так-то». Мы не знаем, как были получены теоремы. Как вавилонянам стала известна теорема Пифагора? У древних египтян была вычислительная арифметика дробей, они умели находить площади плоских фигур, достаточно точно вычислять площадь круга, знали точное правило нахождения объёма усечённой пирамиды. У вавилонян была алгебра (нахождение неизвестного числа по известным) – умели решать квадратные уравнения, системы. Собрание рецептов для решения задач было намного сложнее, чем у египтян, так как у вавилонян была более удобная система счисления. Главные достижения этого периода – возникновение абстрактных понятий (число, фигура, площадь, объём) и замена конкретных условий задач общими – это первичная форма создания алгоритмов. Основная черта II периода - появление доказательства. Вся элементарная математика развилась и сформировалась в период с VI в до н.э. по III в до н.э..Население Древней Греции составляли рабы, рабовладельцы и свободные граждане. Свободные граждане могли принимать участие в выборах, голосовании, благодаря чему, появилось ораторское искусство – искусство логического рассуждения. Логика – это начало математики – получение доказательства путём логического рассуждения. Математика как наука родилась в Греции. Греки выдвинули тезис «Числа правят миром». Или, как сформулировал эту же мысль Галилей два тысячелетия спустя: «книга природы написана на языке математики». Греки проверили справедливость этого тезиса в тех областях, где сумели: астрономия, оптика, музыка, геометрия, позже — механика. Всюду были отмечены впечатляющие успехи: математическая модель обладала неоспоримой предсказательной силой. Одновременно греки создали методологию математики и завершили превращение её из свода полуэвристических алгоритмов в целостную систему знаний. Основой этой системы впервые стал дедуктивный метод, показывающий, как из известных истин выводить новые, причём логика вывода гарантирует истинность новых результатов. Дедуктивный метод также позволяет выявить неочевидные связи между понятиями, научными фактами и областями математики. Начиная с VII в. до н.э. в Древней Греции начали возникать философские школы, которые сыграли огромную роль в развитии и распространении научных знаний. Ионийская школа (основатель - Фалес Милетский) VII-VI в. до н.э. Пифагорейская школа (основатель – Пифагор) VI-V в. до н.э. Афинская школа (основатель Платон) V-IV в. до н.э. Александрийская школа III-II в. до н.э.
Математика — одна из древнейших наук.
Изучением ее законов занимались еще в Древнем Египте, Вавилоне, Древней Индии и Древнем Китае. От математики Древнего Востока до нас дошли только отдельные задачи с решениями и таблицы .Во всей математике Древнего Востока мы нигде не находим никакой попытки дать то, что мы называем доказательством. Мы имеем только предписания в виде правил: «делай то-то, делай так-то». Мы не знаем, как были получены теоремы. Как вавилонянам стала известна теорема Пифагора? У древних египтян была вычислительная арифметика дробей, они умели находить площади плоских фигур, достаточно точно вычислять площадь круга, знали точное правило нахождения объёма усечённой пирамиды. У вавилонян была алгебра (нахождение неизвестного числа по известным) – умели решать квадратные уравнения, системы. Собрание рецептов для решения задач было намного сложнее, чем у египтян, так как у вавилонян была более удобная система счисления. Главные достижения этого периода – возникновение абстрактных понятий (число, фигура, площадь, объём) и замена конкретных условий задач общими – это первичная форма создания алгоритмов.
В Древней Греции рождается наука математика, основанная на строгих доказательствах. Греки выдвинули тезис «Числа правят миром». Или, как сформулировал эту же мысль Галилей два тысячелетия спустя: «книга природы написана на языке математики». Греки проверили справедливость этого тезиса в тех областях, где сумели: астрономия, оптика, музыка, геометрия, позже — механика. Древние греки были удивительно талантливым народом. В те времена Греция состояла из многих мелких государств. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площади, обсуждали его, спорили, а потом голосовали. Они были хорошими "спорщиками". По преданию, в то время сложилось утверждение: " В споре рождается истина!"Именно в этот период развивается исскуство – ораторства. Греки отличались трудолюбием и смелостью. Среди них были отличные строители, мореплаватели, купцы и художники. Они внесли большой вклад в развитие культуры и науки, особенно математики.
Дошедшие до нас из далекого VII в. до н.э. гомеровские поэмы «Илиада» и «Одиссея» дают полное представление о греческой душе и греческой культуре того периода. Она вызывает восхищение и глубокое почтение одновременно. И даже сейчас, в век развитых технологий, невозможно не преклоняться перед достижениями древних греков.
Лишь слегка прикоснувшись к греческой мифологии на уровне школьных знаний, задаешься вопросом: возможно, причина древне-греческого феномена в том, что греки на самом деле жили рядом с богами, учились у них? Может, оттуда пошла в мир высокоразвитая греческая культура? Это можно только предполагать, любуясь нестареющими античными скульптурами Афродиты Милосской и Аполлона Бельведерского.
Легендой и символом врачебного искусства стал Гиппократ, которого глубоко почитают доктора современности. Блестящий оратор IV века Демосфен до сих пор является образцом мастерства риторики, а труды Демокрита продолжают удивлять студентов-философов. Геродоту несомненно принадлежит слава создания истории как науки.
Из курса истории Древнего мира вам наверное хорошно знакомы имена таких древних ученых как Фалес, Гипатия- женщина – математик, философ, врач, после смерти , которой в мире более тысячи лет не было женщины, превзошедшей ее по уму, Пифагор, Аристотель, Эратосфен, Архимед, Платон, Евклид.. …
Сегодня, мы с вами постараемся постичь смысл тезиса последователей Пифагора « Все есть число» и поможет нам в этом умение решать уравнения.
Учитель:Ребята, кто мне напомнит тему предшествующего занятия?
Ученики: Решение задач с помощью уравнений.
Учитель: Пока мы будем готовиться к «путешествию», кто желает проверить свои умения по решению задач с помощью уравнений?
Учитель: раздает несколько карточек для индивидуальной работы.
Индивидуальная работа по теме « Решение задач с помощью уравнений»
Карточки 1 - 4(прилагаются)
Учитель: На дом вам были заданы две задачи, решаемые с помощью уравнений и два уравнения, содержащие дробные коэффициенты.Выполним выборочную проверку домашнего задания.Ребята,у кого из вас возникли затруднения при выполнении заданий домашней работы?На слайде показаны решения к задачам. Вы можете сверить полученные решения с образцом возможного правильного решения. ( слайд 6-7 )
Учитель: Вспомним основные понятия ,изученные нами и необходимые нам при решении задач и уравнений .
Учитель: А теперь сформулируем эти понятия и определения. Посмотрите на слайд ( слайд 8-10 )
Учащиеся отвечают на вопросы.
Учитель: Вспомним алгоритм решения задач с помощью уравнения.
Ученики. ( слайд 10 )
Обозначают некоторое неизвестное число буквой х и, используя условие задачи, составляют уравнение;
Решают это уравнение;
Истолковывают полученный результат в соответствии с условием задачи.
Учитель: Как уже упоминалось ранее, именно в Древней Греции родилась наука математика, основанная на строгих доказательствах. Этот важнейший скачок в науке относят к VI-V вв. до н.э. Отцом греческой науки называют Фалеса Милетского (ок. 625-547 гг. до н.э.). В математике Фалес доказал несколько важных теорем, предложил способы вычисления высоты фигуры по ее тени и определения расстояния до корабля на море. (Основатель – ионийской ( милетской) школы Фалес)
Еще одним из известнейших древнегреческих ученых был Пифагор. Пифагор, основатель Пифогорийской школы — личность легендарная, и достоверность дошедших до нас сведений о нём проверить невозможно. Пифагор родился на острове Самос. Видимо, он, как и Фалес, много путешествовал и тоже учился у египетских и вавилонских мудрецов. Вернувшись около 530 г. до н. э. в Великую Грецию (район южной Италии) он основал нечто вроде тайного духовного ордена. Именно он выдвинул тезис «Числа правят миром», и с исключительной энергией занимался его обоснованием. В начале V в. до н. э., после неудачного политического выступления, пифагорейцы были изгнаны из Южной Италии, и союз прекратил свое существование, однако популярность учения от рассеяния только возросла. Пифагорейские школы появились в Афинах, на островах и в греческих колониях, а их математические знания, строго оберегаемые от посторонних, сделались общим достоянием. В молодости он путешествовал по Египту и Вавилону, изучая мудрость жрецов, а около 530 г. до н.э. переехал в Кротон, где основал свою школу, знаменитый пифагорейский союз. Для развития у своих учеников неординарного самостоятельного мышления, в школе особое внимание уделялось замысловатым вопросам. ( слайд 11-13 )
Учитель: А сколько было учеников у Пифагора? Такой же вопрос однажды на пиру задал Пифагору тиран острова Самос Поликрат.
Задача 1. ( слайд 14-16 )
«Охотно скажу тебе, о Поликрат, - отвечал Пифагор. - Половина моих учеников изучает прекрасную математику, четверть исследует тайны вечной природы, седьмая часть молча упражняет силу духа, храня в сердце учение. Добавь еще к ним трех юношей, из которых Теон превосходит прочих своими способностями. Столько учеников веду я к рождению вечной истины».
Учитель: Так сколько же учеников было у Пифагора? Что нам известно? Каким способом будем решать задачу?
Ученики: С помощью уравнения.
Учитель: Как вам известно краткую запись к задаче можно приводить и в текста, и в табличном виде.Кто из учащихся пойдет к доске?
Ученик: Выходит к доске, выполняет решение задачи.
Рекомендуемая краткая запись к задаче о количестве учеников Пифагора.
| текст задачи | математическое выражение |
| колич-во учеников Пифагора | х |
| изучают математику | 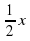
|
| исследователи тайн природы | 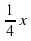
|
| упражняют силу духа | 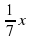
|
| юноши | 3 |
Уравнение, составленное по условию задачи. Решение уравнения. ( слайд 16)
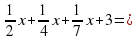 х. Приведем дроби к общему знаменателю НОК ( 2, 4, 7) = 28;
х. Приведем дроби к общему знаменателю НОК ( 2, 4, 7) = 28;
14х + 7х + 4х + 84 = 28х;
25х -28х = -84;
-3х = - 84;
х = 28.
Итак, учеников в школе у Пифагора было 28 .
Ответ: 28 учеников.
Учитель: Почти все математики древности занимались уравнениями. Много внимания им уделял древнегреческий ученый Диофант. ( слайд 17 -19) О Диофанте известно очень мало. Есть основание полагать, что он жил около III в. н.э. Одна группа уравнений, так называемые неопределенные уравнения, до сих пор называются диофантовыми уравнениями ( с двумя неизвестными). Именно для них он нашел способ решения. Часто такие уравнения или задачи, сводимые к составлению таких уравнений встречаются среди олимпиадных задач по математике.
Скудные сведения о Диофанте может дополнить нам лишь надпись на надгробном камне, сформулированная задача в стихах.
Задача № 2.( слайд 18)
Здесь погребен Диофант, а камень могильный
При счете искусном расскажет нам,
Сколь долог был его век.
Велением бога он мальчиком был шестую часть своей жизни,
В двенадцатой части прошла его юность.
Седьмую часть жизни прибавим – пред нами очаг Гименея,
Пять лет протекло и прислал Гименей ему сына
Но горе ребенку! Едва половину он прожил
Тех лет, что отец, скончался несчастный.
Четыре года страдал Диофант от утраты той тяжкой
И умер, прожив для науки. Скажи мне,
Скольких лет достигнув, смерть восприял Диофант?
Учитель: Есть желающие выйти и решить задачу?
Ученик: Выходит к доске составляет краткую запись и решает уравнение.
| период его жизни | математическое выражение | возраст Диофанта. |
| Часть шестую его представляло прекрасное детство | 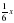
| 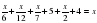
|
| Двенадцатая часть протекла еще жизни – покрылся Пухом тогда подбородок. | 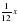
|
| Седьмую в бездетном Браке провел Диофант. | 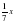
|
| Прошло пятилетие;он Был осчастливлен рождением прекрасного первенца сына, | 5 |
| Коему рок половину лишь жизни прекрасной и светлой Дал на земле по сравнению с отцом | 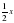
|
| И в печали глубокой Старец земного удела конец восприял, переживши Года четыре с тех пор, как сына лишился. | 4 |
Решение уравнения. ( слайд 19)
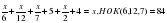
14х+7х+12х+420+42х+336=84х;
33х+42х-84х= -336 – 420;
-9х = - 756;
х = 84.
Итак, возраст Диофанта составил 84 года.
Ответ: возраст Диофанта 84 года.
Учитель: № 3 Задача о статуе Минервы( задача Метродора)
Сохранилась “Греческая антология” в форме сборника задач, составленных в стихах, главным образом гекзаметром, которым, как известно, написаны знаменитые поэмы Гомера (IX-VIII вв. до н.э.) “Илиада” и “Одиссея”. “Греческая антология” была написана в VI в. н.э. грамматиком Метродором.Лексическое значение слова « антология» из словаря С.Ожегова- сборник избранных художестченных произведений разных авторов.» Греческая антология» содержит 48 задач в стихотворной форме,некоторые из них мы разберем сегодня. В “Греческой антологии” содержится задача о статуе Менервы-богини мудрости, покровительнице наук, искусств и ремёсел, задача о возрасте Диофанта, задача об Эроте и яблоках и задача о статуе Полифема
( слайд 20-21 )
Я – изваянье из злата. Поэты то злато
В дар принесли: Харизий принёс половину всей жертвы,
Феспия часть восьмую дала; десятую Солон.
Часть двадцатая – жертва певца Фемисона, а девять
Всё завершивших талантов – обет, Аристоником данный.
Сколько же злата поэты все вместе в дар принесли?
Учитель: Пусть каждый из вас еще раз перечитает внимательно эту задачу. Похожа ли она на задачу о школе Пифагора?
Ученики: Похожа.
Учитель: Кто из учеников пойдет к доске выполнять решение задачи?
Ученик: Выходит к доске, по тексту задачи составляет краткую запись.
Рекомендуемая таблица
|
| математическое выражение | общее количество золота |
| дар Харизия | 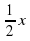
| х |
| Феспии | 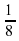 х х
|
| Солона | 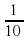 х х
|
| певца Фемисона | 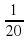 х х
|
| Аристоника | 9 |
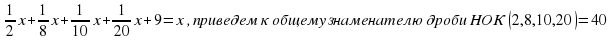 ( слайд 22)
( слайд 22)
20х + 5х+4х+2х+360 =40х;
-9х = -360;
х= 40.
Итак, вдар , на строительство статуи ушло 40 талантов.
Ответ : 40 талантов.( 1 талант = 16,8 кг золота)
Учитель: А что такое талант? ( слайд 22 )В античные времена существовала единица массы, которая называлась «талант»
( «талант»- крупнейшая денежная единица в Древней Греции и она была равна примерно 16,8 кг.) Давайте подсчитаем, сколько весила статуя Минервы в килограммах?
Ученики: Приблизительно 672 кг.
Учитель: Вот такая тяжелая статуя Минервы, богини мудрости.
Учитель: Задача № 4 Статуя Полифема.
Вот Полифема циклопа из меди статуя отлита.
Руку, уста и единое око ваятель сделал на диво.
Скрывши в них трубы:
водой великан истекает как будто.
И в настоящее время влагу уста изливают.
Хитрое в трубах устройство: ведущая в руку способна
Весь водоем до краев через три дня переполнить.
Оку – достаточно дня, а устам и всего лишь две пятых,
Вместе все три водоем скоро ли могут наполнить?
Учитель: Решение .
Весь объем работы - 1
Труба в руке за 1 час наполнит – 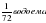
Труба в оке за 1 час наполнит - 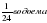
Труба в устах за 1 час наполнит – 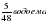 .
.
Уравнение.
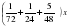 =1;
=1;
( 2+6+ 15)х=144;
х=144: 23;
х=6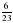 .
.
Итак, водоем наполнится за 6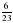 ч.
ч.
Ответ : 6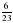 ч. .
ч. .
Учитель: А теперь, чтобы вы смогли убедиться в том, что полученные вами знания и умения можете применять в практической деятельности,предлагаю вам самостоятельную работу.
Самостоятельная работа по теме « Решение задач с помощью уравнений»
Вариант 1 .(Вариант 2.)
( задания прилагаются)
( слайд 25 )
Ученики: после окончания самостоятельной работы прередают тетради с работами на предение парты.
Учитель: А напомните-ка мне, кто ведал науками и искусствами по предствалениям древних греков? Подскажу. Это мифические женские существа.
Ученики: Музы.( слайд 26-28 )
Учитель: Верно. Деятельность ученых протекала в учреждениях, которые назывались музеумами (или музеями) — жилищами муз. Обитали музы на горе Геликон.Можете ли вы назвать всех муз Древней Греции или хотя бы их количество? Сохранилась древняя поэтическая задача, в которой бог любви Эрот жалуется богине красоты и любви Киприде на муз: 
Видя, что плачет Эрот, Киприда его вопрошает:
«Что тебя так огорчило, ответсвуй немедля!»
«Яблок я нес с Геликона немало, -Эрот отвечает, -
Музы, отколь ни возьмись, напали на сладкую ношу.
Частью двенадцатой вмиг овладела Евтерпа, а Клио
Пятую долю взяла. Талия — долю восьмую.
С частью двадцатой ушла Мельпомена. Четверть взяла Терпсихора.
С частью седьмою Эрато от меня убежала.
Тридцать плодов утащила Полимния. Сотня и двадцать
Взяты Уранией; триста плодов унесла Каллиопа.
Я возвращаюсь домой почти что с пустыми руками.
Только полсотни плодов мне оставили музы на долю.
Учитель: Эту задачу я предлагаю вам решить дома самостоятельно. Пока я раздаю вам карточки с текстом задачи, откройте дневники и запишите домашнее задание: ( слайд 29 )
Задача о греческих музах;
№ 407( старинная русская задача)
№ 374 ( второй столбик) ( решить уравнения, содержащие дробные коэффициенты)
Учитель: Что ж, наше путешествие в мир Древней Греции подошло к концу. Я предлагаю вам следующее задание
« Закончите предложение» ( слайд 30-31 )
Учитель: Ребята, поднимите смайлик, который выражает ваше состояние на конец урока.
Всем спасибо за работу, урок окончен!

Учитель математики : Тадтаева З.З.
14 января 2015г.
г. Владикавказ.






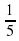 этого набора подарил сестре,
этого набора подарил сестре, 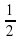 - брату, а оставшиеся 3 марки оставил себе. Сколько марок было в наборе?
- брату, а оставшиеся 3 марки оставил себе. Сколько марок было в наборе?
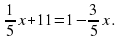
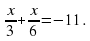
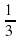 , то в корзине осталось 20 штук яблок .Сколько яблок было в корзине первоначально?
, то в корзине осталось 20 штук яблок .Сколько яблок было в корзине первоначально?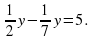
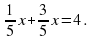

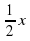
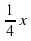
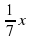
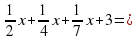 х. Приведем дроби к общему знаменателю НОК ( 2, 4, 7) = 28;
х. Приведем дроби к общему знаменателю НОК ( 2, 4, 7) = 28;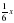
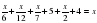
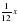
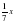
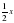
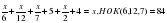
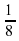 х
х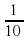 х
х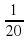 х
х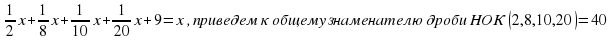 ( слайд 22)
( слайд 22)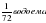
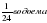
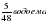 .
.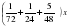 =1;
=1;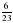 .
.