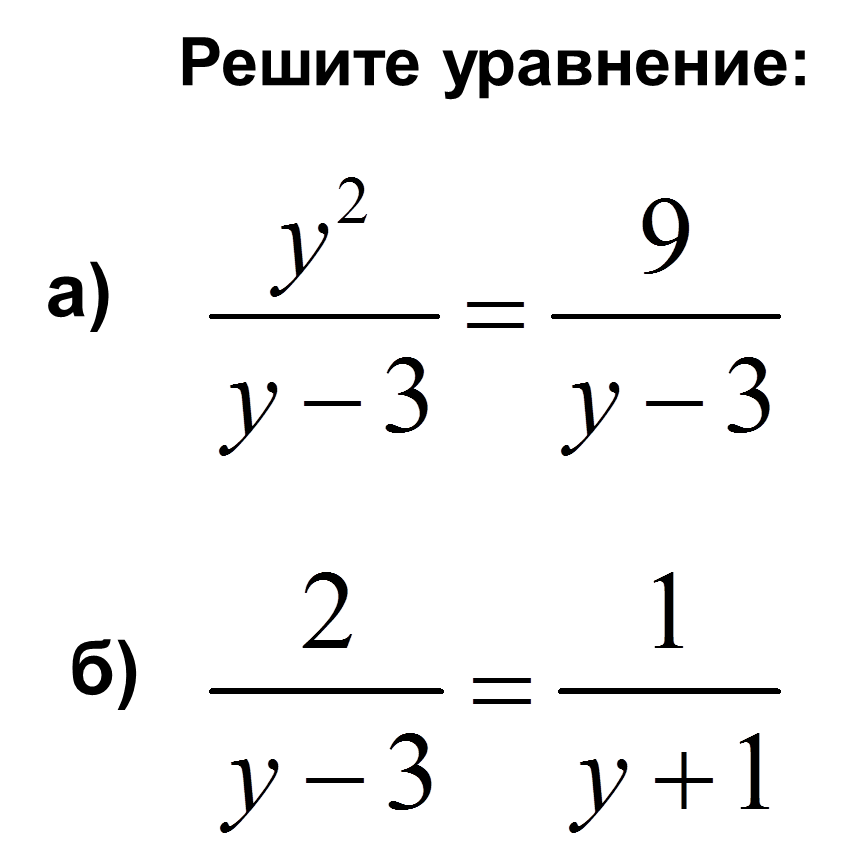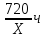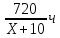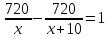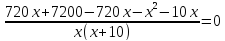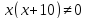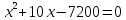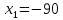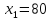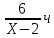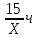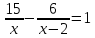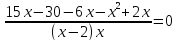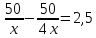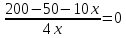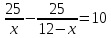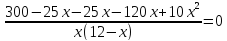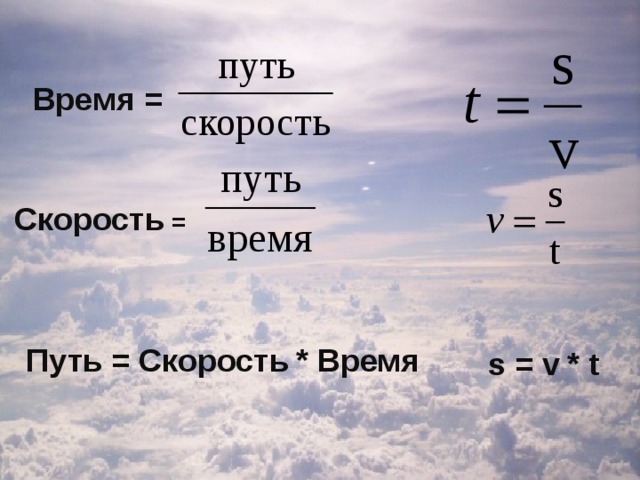Просмотр содержимого документа
«план откр урока»
Решение задач с помощью рациональных уравнений. Алгебра (8-й класс)
Цели урока:
- отработка навыков решения задач на составление дробных рациональных уравнений;
- знакомство с геометрическим способом решения уравнений;
- развитие способности к содержательному обобщению и рефлексии;
- развитие алгоритмического мышления;
- повышение интереса к решению математических задач
- показать связь с другими предметами, с жизнью.
Ход урока:
Использование презентации
Пусть математика сложна,
Ее до края не познать
Откроет двери всем она,
В них только надо постучать.
Чтобы двери в мир математики открывались как можно легче мы сегодня будем учиться…
Тема нашего урока: Решение задач с помощью рациональных уравнений.
1.Актуализация опорных знаний. Разминка.

Ответы: а)2; б)нет реш в) о или -4; г) -11 и -2
А) 4 и 3 б) -7 и 5 в) 8 и 7
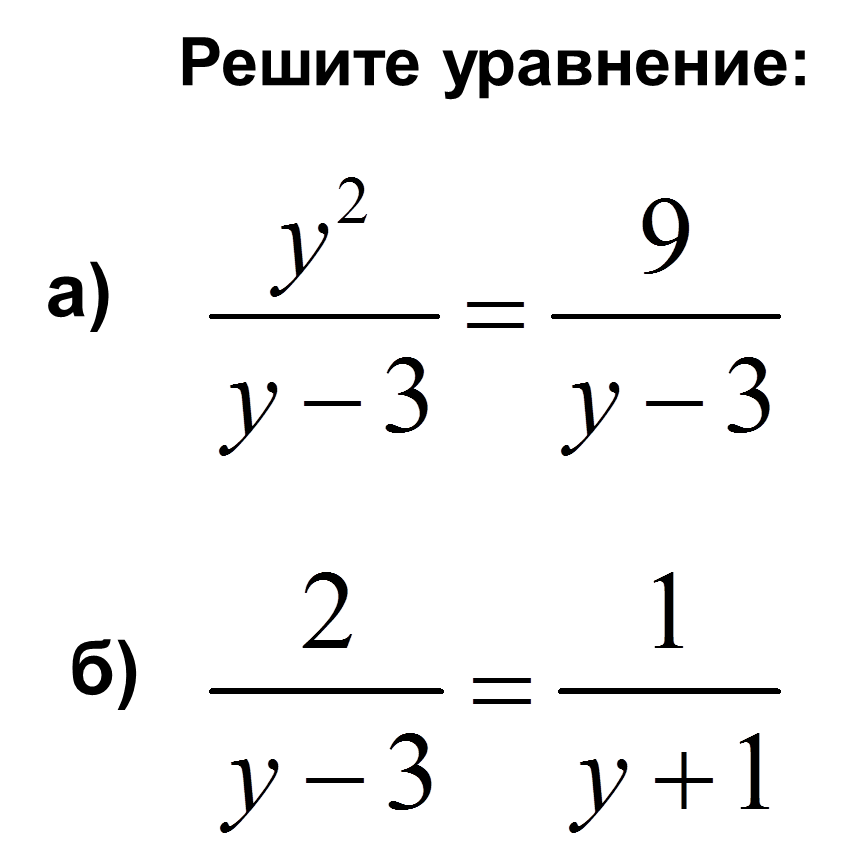
Ответы : а) -3; б) -5
2. Повторяем формулы : путь – время – скорость
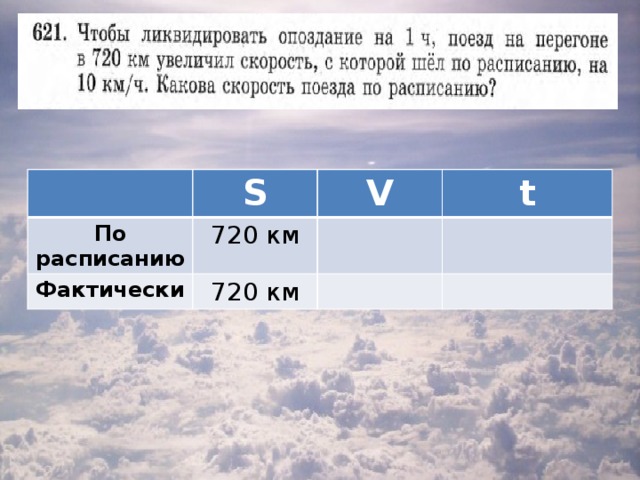
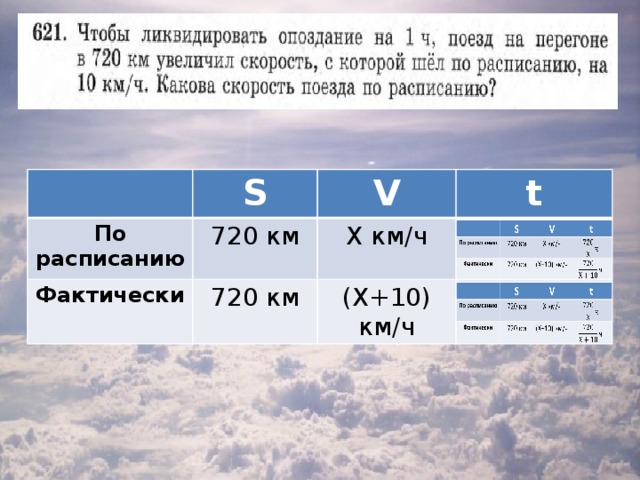
3. Работа с учебником: задача №621, стр 146

|
| S | V | t |
| По расписанию | 720 км | Х км/ч | 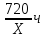
|
| Фактически | 720 км | (Х+10) км/ч |
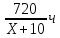
|

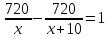
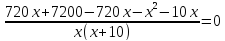
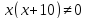
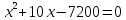
Корни по т. Виета
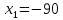
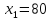
Ответ: 80 км/ч.

|
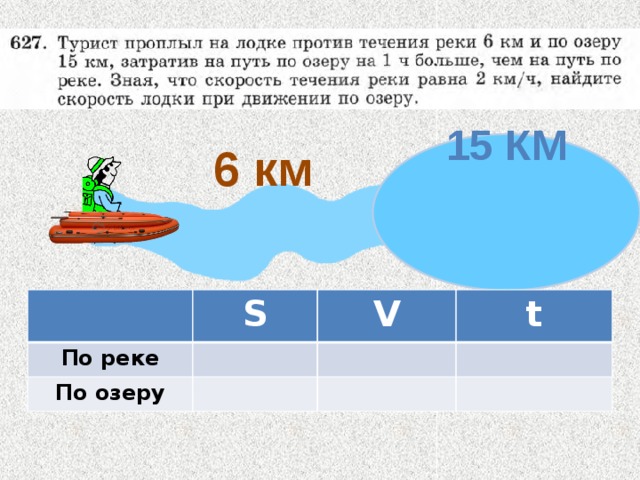
| S | V | t |
| По реке | 6 км | (Х-2)км/ч | 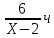
|
| По озеру | 15 км | Х км/ч | 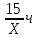
|
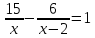
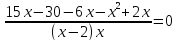

X2-11x+30=0
X1=5; x2=6
Задача. Разбираем условие задачи. Выполняют самостоятельно.
Одновременно п.В.Фиагдон в г. Владикавказ выехали велосипедист и автомобиль. Скорость автомобиля в 4 раза больше скорости велосипедиста, и поэтому автомобиль приедет в г. Владикавказ на 2 часа 30 минут раньше. Какое время понадобится велосипедисту на путь из В. Фиагдона до Владикавказа, если расстояние между ними 50 км.
1)
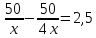
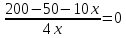
Х=15 км/ч
2) 50/15=3 часа 20 минут
Самостоятельная работа № 702
| 702 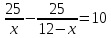
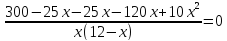
Х1=15 не явл. Реш. Х2=2 Ответ: 2 км/ч
|
Итог урока: Общеизвестно высказывание: “Решение математической задачи можно сравнить со взятием крепости”.
После данного урока решение большинства задач, я надеюсь, со взятием крепости уже не ассоциируется. Вы согласны со мной, ребята?
Домашнее задание: № 628, № 629
Просмотр содержимого презентации
«откр урок 8 кл»