Урок геометрии 7 класс

Раздел 7.2В: Треугольники.

Школа: № 66

Дата: 11.12.2018

Ф.И.О. учителя: Усачёва Е.А.

Класс: 7 «Д»

Количество присутствующих:

Количество отсутствующих:

Тема урока:

Третий признак равенства треугольников

Тип урока:

Изучение новой темы

Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):

7.1.1.21

знать и доказывать признаки равенства треугольников;

7.1.1.22

применять признаки равенства треугольников при решении задач на вычисление и на доказательство;

7.1.1.23

применять свойства и признаки равнобедренного треугольника;

7.1.1.24

применять свойства равностороннего треугольника при решении задач;

Цель урока:

• Знать и доказывать третий признак равенства треугольников (по трём сторонам).

• Формировать навыки доказательных рассуждений с помощью аксиом и теорем.

• Применять третий признак равенства треугольников при решении задач.

• Знать определение равнобедренного треугольника и его свойства;

• Применять свойства равнобедренного треугольника при решении задач;

Критерии оценивания:

Учащийся достиг цели обучения, если

Знает доказательство третьего признака равенства треугольников.

Умеет применять третий признак равенства треугольников при решении задач.

Языковые цели

Учащиеся будут:

• комментировать ход решения задачи;

• оперировать понятиями и терминами раздела;

• формулировать признаки равенства треугольников;

• описывать построение чертежа по тексту задачи;

• описывать данные чертежа;

Межпредметные связи

Знания, полученные на этом уроке, помогут решать базовые геометрические задачи, используемые в физике, в астрономии, на практике.

Предварительные знания

Знание аксиом, в которых отражены основные свойства простейших фигур. Умение измерять и строить углы с помощью транспортира. Знать определение равных фигур. Знать первый и второй признаки равенства треугольников.Знать свойства и признаки равнобедренного треугольника.

Ход урока

Этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало урока:

5 мин

Организационный момент

1. Приветствие класса.

2. Проверка готовности класса к уроку.

3. Деление на группы;

4. Проверка домашней работы:

№ 11.2

Дано:

AB=DC

BC=AD

Д-ть:

B = D

Д-во:

Рассмотрим ∆АВС и ∆ ADC

AB=DC, BC=AD (по условию); AC-общая =

= ∆АВС и ∆ ADC (по 3 признаку) = D ■

№ 11.5

Дано:

AB=АD

DC=ВС

Д-ть:

АС - биссетриса D

Д-во:

Рассмотрим ∆DAC и ∆ BAC .

AB=AD, DC=BC- по условию

AC-общая = ∆DAC=∆ BAC =

= АС-биссектриса D ■

№ 11.6

Дано:

АD=ВС

АС=ВD

Д-ть:

D=

Д-во:

Рассмотрим ∆ВАD и ∆АВС .

AD=ВС, АC=BD- по условию

AВ-общая = ∆ВАD = ∆АВС .= D=

Презентация

Середина урока

30 минут

1. Актуализация знаний:

1.1ИГРА «Верно – неверно» (Верно – зелёный кружок, неверно – красный):

1. Верно ли, что треугольник у которого боковые стороны равны называется разносторонним? (Нет)

2. Верно ли, что медиана в равнобедренном треугольнике является биссектрисой и высотой? (Да)

3. Верно ли, что если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны? (Да)

4. Верно ли, что если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники равны? (Нет)

5. Верно ли, что если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны? (Нет)

6. Верно ли, что если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны? (Да)

7. Верно ли, что если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны? (Да)

1.2 Математический диктант:

Укажите номера рисунков, на которых треугольники равны по:

• первому признаку:

• второму признаку:

• третьему признаку:

Ответы на диктант:

• По двум сторонам и углу между ними: 2,8,9,13.

• По стороне и прилежащим к ней углам: 3,6,12,14.

• По трём сторонам: 1,10,11.

Решение задач по готовому чертежу (задача №1, задача №2, задача№3)

- Используя, полученные знания и навыки, продолжим

решение задач.

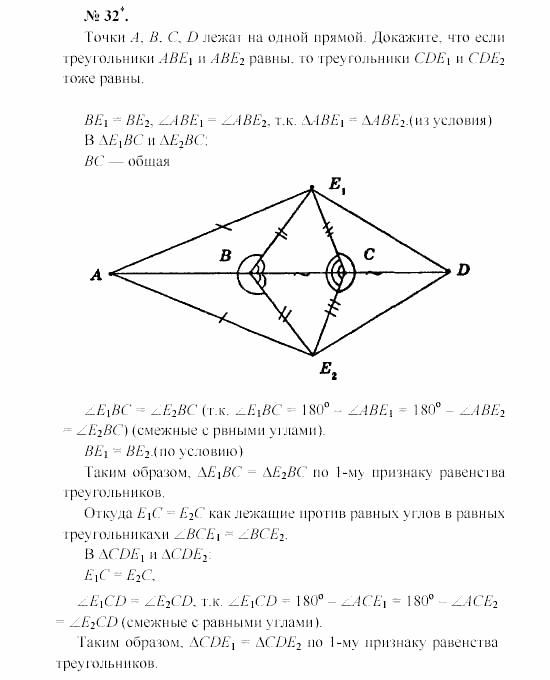
№1 (устно). По готовому чертежу докажите равенство треугольников.

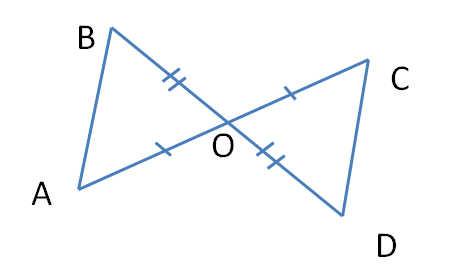
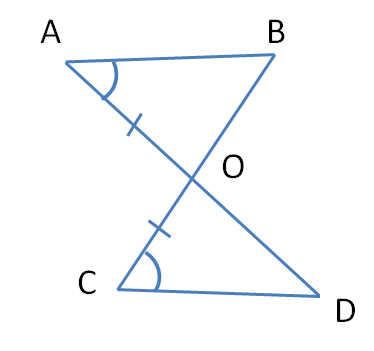
№2 (устно).

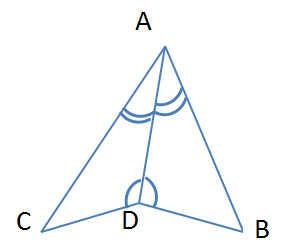
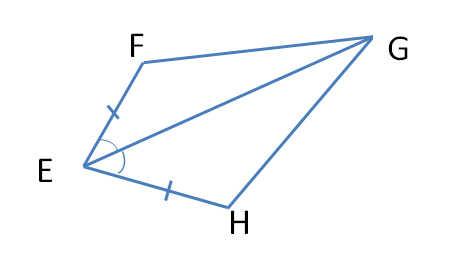
№3 (устно).

3. Работа по учебнику: стр. 64-65 №№ 11.8, 11.10,

№ 11.8

∆ADO =∆ CDO равны ( по 3 сторонам)

=,

∆ABD=∆ CBD (по 2 сторонам и углу между ними : BD общая, AD=CD по условию, равенство углов доказано выше) =АВ=ВС. ■

№ 11.10

∆ АВС=∆CDA = AD=BC, AB=DC, AC-общая(по 3 признаку)

Рассмотрим ∆BCD и ∆DAB AD=BC, AB=DC, BD-общая(по 3 признаку) ■

Конец урока:

5 минут

1. Подведение итогов урока. Рефлексия.

Острова

На доске вывешиваются рисунки островов. В конце урока ученики знаками отмечают. По какому острову путешествовал каждый. Острова могут дорисовываться. Учитель может спросить, почему выбран именно этот остров

Остров скуки

остров открытий

.

Остров радости

2. Постановка домашней работы: §11 теорема, №№ 11.9, 11.12

Дифференциация

Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?

Оценивание

Как Вы планируете проверить уровень усвоения материала учащимися?

Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.

Здоровье и соблюдение техники безопасности

Здоровье сберегающие технологии.

Используемые активные виды деятельности.