Тема урока геометрии « Решение треугольников»
(Учебник для 7-9 кл. сред.шк./Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М.: Просвещение, 2016.)
Предмет: геометрия
Класс: 9
Тип урока: закрепления изученного материала
Цель урока: научиться решать произвольные треугольники
Образовательные задачи урока:
закрепить знания по теме «Соотношения между сторонами и углами треугольника »;
разработка алгоритмов решения основных типов задач;
выработать умение применять созданные алгоритмы при решении базовых задач;
развивать математическую культуру речи;
формировать у учащихся мотивацию к изучению предмета.
Развивающие задачи урока:
развивать математическое мышление;
совершенствование навыков само- и взаимно- обучения;
совершенствование навыков самооценки результатов деятельности;
развитие навыка постановки образовательной цели ;
развивать познавательную и аналитическую деятельность.
Воспитательные задачи урока:
формировать ответственное отношение к результатам учебного труда;
совершенствовать умение самоорганизации и самоконтроля;
развивать умение индивидуальной и групповой продуктивной работы;
воспитывать дисциплинированность при организации работы на уроке.
Оборудование:
Компьютер, проектор.
Здоровье сберегающие составляющие урока:
четкая последовательность урока ;
уровневый подход к организации учебной деятельности;
участие каждого ученика в результативной работе на уроке;
соблюдение режима работы ИКТ;
доброжелательная обстановка урока.
Методы обучения: эвристическая беседа, репродуктивный, объяснительно-иллюстративный, исследовательский, проблемный.
Формы организации учебной работы: фронтальная, работа в группах, индивидуальная, метод джиксо.
Структура урока
Организационный момент. Целеполагание.
Актуализация знаний. Устная работа. Экзамен –опрос.
1. Какую фигуру называют треугольником?
2. Перечислите элементы треугольника.
3. Назовите виды треугольников по углам.
4. Назовите виды треугольников по сторонам.
4. Как построить единичную полуокружность?
5. Объясните, что такое синус угла α из промежутка 00 ≤ α ≤ 1800
6. Объясните, что такое синус угла α из промежутка 00 ≤ α ≤ 1800
7. Что называется тангенсом угла α?
8. Для какого значения тангенс α не определен и почему?
9. Назовите основное тригонометрическое тождество.
10. Сформулируйте теорему о площади треугольника.
11. Сформулируйте теорему синусов.
12. Сформулируйте теорему косинусов.
13. Сформулируйте теорему о сумме углов треугольника.
14. Что значит решить треугольник?
(слайды 3-9)
Основные этапы урока:
Работа над созданием алгоритма и его проверкой.
а) Введение в тему
Треугольник является одной из основных геометрических фигур. Многие из известных фигур (параллелограмм, трапеция, ромб, квадрат, прямоугольник и произвольный многоугольник) можно разбить на треугольники. Поэтому важно уметь решать треугольники.
Во всяком треугольнике есть шесть основных элементов: три стороны и три угла. В теме «Решение треугольников» ставится вопрос о том, как, зная одни из основных элементов, найти другие.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Решение данных задач основано на использовании теорем синусов и косинусов, теореме о сумме углов треугольника.
Причем, при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов. Почему?
Все задачи на решение треугольника сводятся к трем видам:
По двум сторонам и углу между ними.
По стороне и двум прилежащим углам.
По трем сторонам.
(слайды 10-12)
б). Решение задач
К доске по очереди приглашаются ученики для решения одной задачи из четырех предложенных выбранных учеником наугад.
(Презентация слайд 13-17 )

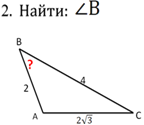


в) работа в разно- уровневых группах
в) Самостоятельное решение задач с выбором ответа (слайд 18)
Каждому ученику необходимо решить задачу и найти на общем столе карточку с правильным ответом. Тот ученик, который первым решает задачу, становится консультантом и помогает решить задачу своей группе.
| 1. Стороны треугольника 7см и 3см, а угол между ними 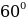 . Найдите третью сторону треугольника. . Найдите третью сторону треугольника. а) 2см б) 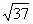 см в) см в)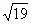 см г) 4 см см г) 4 см
|
| 2. Определите вид треугольника (относительно его углов), если его стороны равны 7, 8 и 12. а) остроугольный б) прямоугольный в) тупоугольный
|
| 3. Найдите сторону треугольника, лежащего против угла в 300. 
а) 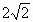 дм б) дм б) 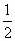 дм в) дм в) 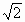 дм г) дм г) 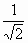 дм дм
|
| 4. У треугольника две стороны равны 5дм и 4дм, а угол между ними равен 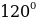 Найдите третью сторону треугольника. Найдите третью сторону треугольника. а) 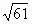 б) б) 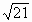 в) 24 г) 21 в) 24 г) 21
|
| 5.В треугольнике АВС АВ=5см , ВС=8см, угол С равен 450 . Найти синус угла А. а) 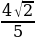 б) б)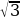 в) в)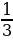 г) г) 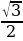
|
Ответы к задачам.

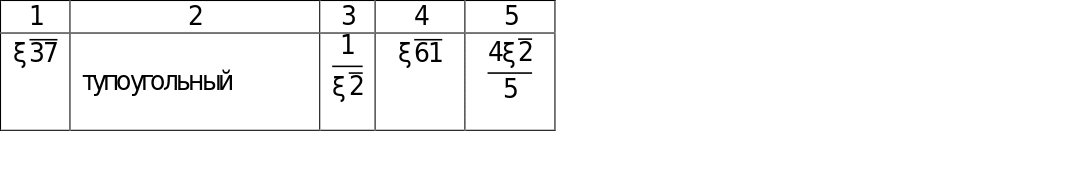
Из истории математики (слайды 19-22)
Термин «тригонометрия» дословно означает «измерение треугольников». Его ввел в употребление в 1595 году немецкий математик и богослов Питиск, автор учебника по тригонометрии и различных таблиц.
Тригонометрия – раздел математики, который изучает зависимость между углами и сторонами треугольника.
Первые отрывочные сведения по тригонометрии сохранились на клинописных табличках Древнего Вавилона. А в Древней Греции во 2 веке до н.э. астроном Гиппарх из Никеи составил таблицу для определения соотношений между элементами треугольника. По существу это была первая таблица синусов.
К концу 13 века ученые исламского мира уже оперировали тригонометрическими функциями, открыли и доказали несколько важных теорем, использовали окружность единичного радиуса. Арабские математики составили исключительно точные таблицы синусов и тангенсов с шагом в 1′. Особенно большое влияние на развитие тригонометрии оказал «Трактат о полном четырехугольнике» астронома Насир ад-Дин ат-Туси.
Это было первое в мире сочинение, в котором тригонометрия трактовалась как самостоятельная наука.
 Насир ад-Дин ат-Туси ( 1201 -1274)
Насир ад-Дин ат-Туси ( 1201 -1274)
Трактат Ат-Туси произвел огромное впечатление на немецкого астронома и математика Иоганна Мюллера (1436-1476). Современники больше знали его под другим именем. Это имя переводится на латинский язык как название его родного города Кёнигсберга.
Иоганн Мюллер – автор первых печатных астрономических таблиц, где применялись тригонометрические знания, которыми пользовались Васко да Гама, Христофор Колумб и другие мореплаватели.
 Иоганн Мюллер (1436—1476)
Иоганн Мюллер (1436—1476)
Труд Региомонтана «О треугольниках всех родов пять книг» сыграл в европейской математике огромную роль – дал толчок к бурному развитию тригонометрии в Европе. Дальнейшее ее развитие пошло по пути накопления и систематизации формул, уточнение основных понятий, становления терминологии и обозначений.
Региомонтан основал одну из первых астрономических обсерваторий в Европе (г. Нюрнберг, 1471г.)

Практическое применение. (слайды 23-25)
Тригонометрические функции могут быть использованы для проведения различных измерительных работ на местности. Об этом мы поговорим на следующем уроке.
А сейчас проведём небольшую спасательную операцию. Класс делится на две команды судна «Стремительный и судна «Быстрый». Выбираем капитана в каждой команде. Надо выяснить какая команда первой придёт на помощь?
Решение задачи с практическим содержанием.
На судна “Стремительный” и “Быстрый” поступил сигнал бедствия с судна “Звезда” .Радиопеленгатор судна “Стремительный” определил пеленг в 550, а судна “Быстрый” - 1000.Кто первым придет на помощь “Звезде”, если скорость “Стремительного” равна 60 км/ч, а “Доброго”- 45 км/ч?
Завершение урока. (слайды 26-27)
Закончим урок словами великого итальянского ученого Галилео Галилея: “Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать”.
Организация рефлексии и обратной связи. (Синквейн)
Подведение итогов работы
VII. Домашнее задание
а) п. 99, №1025(г,е), №1030
6








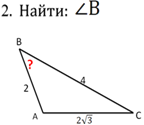


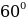 . Найдите третью сторону треугольника.
. Найдите третью сторону треугольника.
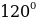 Найдите третью сторону треугольника.
Найдите третью сторону треугольника.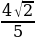 б)
б)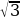 в)
в)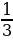 г)
г) 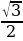

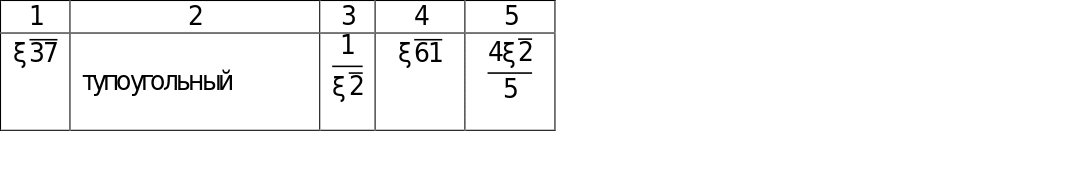
 Насир ад-Дин ат-Туси ( 1201 -1274)
Насир ад-Дин ат-Туси ( 1201 -1274) Иоганн Мюллер (1436—1476)
Иоганн Мюллер (1436—1476)










