Просмотр содержимого документа
«Урок геометрии в 10 классе Тема: «Двугранный угол. Линейный угол двугранного угла»»

Двугранный
угол

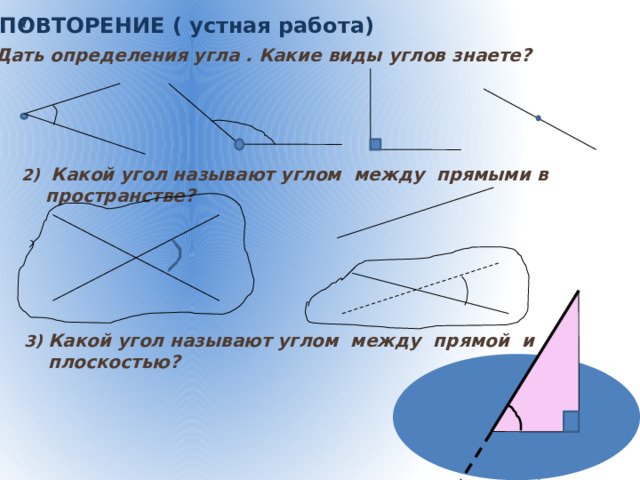
ПОВТОРЕНИЕ ( устная работа)
1) Дать определения угла . Какие виды углов знаете?
2) Какой угол называют углом между прямыми в пространстве?
3) Какой угол называют углом между прямой и плоскостью?
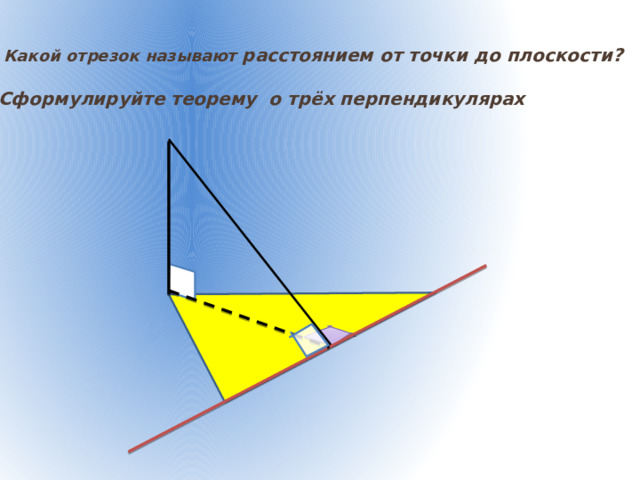
4) Какой отрезок называют расстоянием от точки до плоскости?
5) Сформулируйте теорему о трёх перпендикулярах
II.
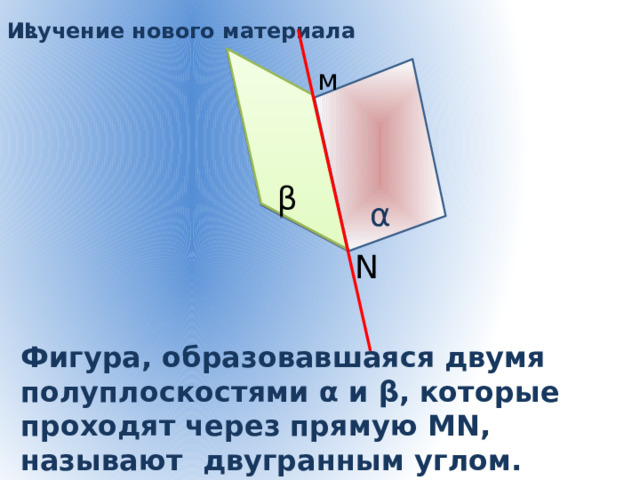
Изучение нового материала
β
м
α
N
Фигура, образовавшаяся двумя полуплоскостями α и β, которые проходят через прямую МN, называют двугранным углом.
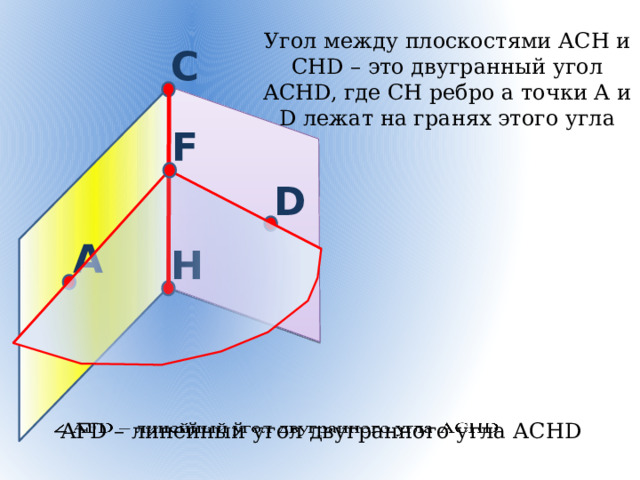
Угол между плоскостями АСН и СНD – это двугранный угол АСНD, где СН ребро а точки А и D лежат на гранях этого угла
C
F
D
A
H
AFD – линейный угол двугранного угла АCHD
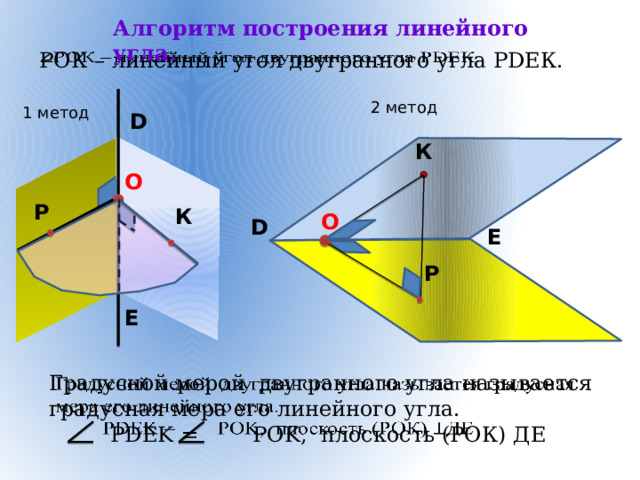
Алгоритм построения линейного угла.
РОК – линейный угол двугранного угла РDEК.
2 метод
1 метод
D
К
O
Р
К
O
D
E
Р
E
Градусной мерой двугранного угла называется градусная мера его линейного угла.
PDEK = POK, плоскость (РОК) ДЕ
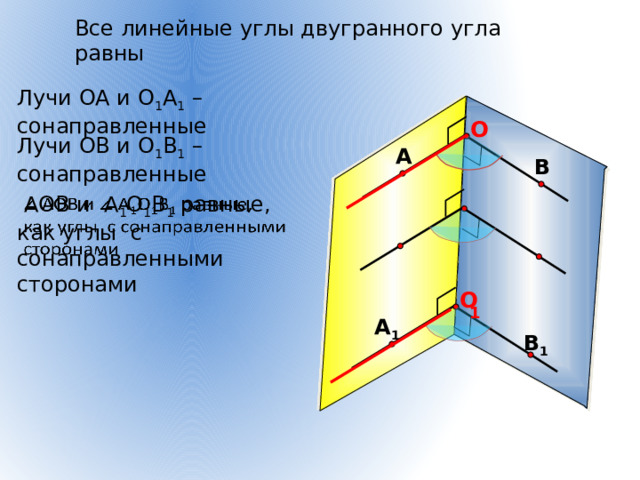
Все линейные углы двугранного угла равны
Лучи ОА и О 1 А 1 – сонаправленные
O
Лучи ОВ и О 1 В 1 – сонаправленные
А
В
АОВ и А 1 О 1 В 1 равные,
как углы с сонаправленными сторонами
O
1
А 1
В 1
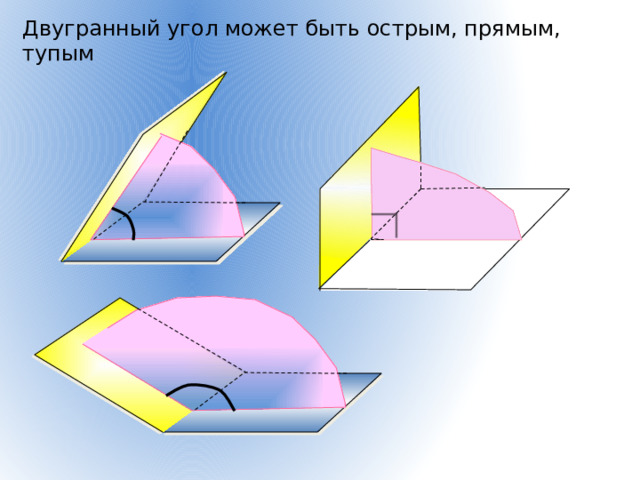
Двугранный угол может быть острым, прямым, тупым
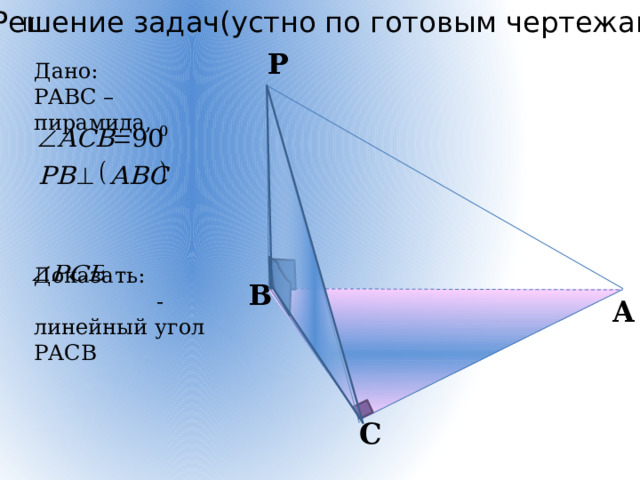
Решение задач(устно по готовым чертежам)
Р
Дано:
РАВС – пирамида,
Доказать:
- линейный угол РАСВ
В
A
С
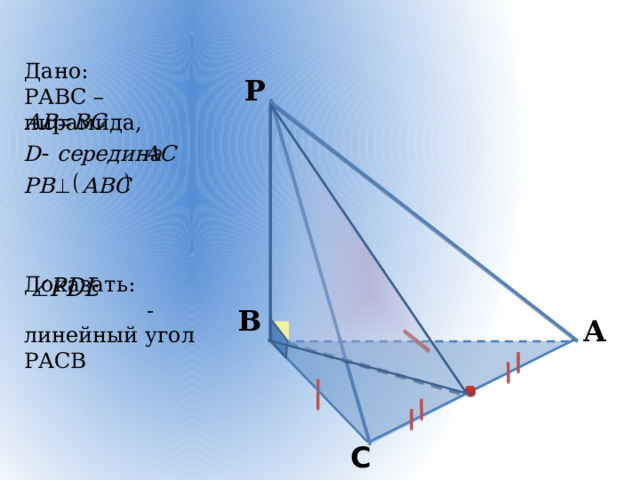
Дано:
РАВС – пирамида,
Доказать:
- линейный угол РАСВ
P
В
А
D
С
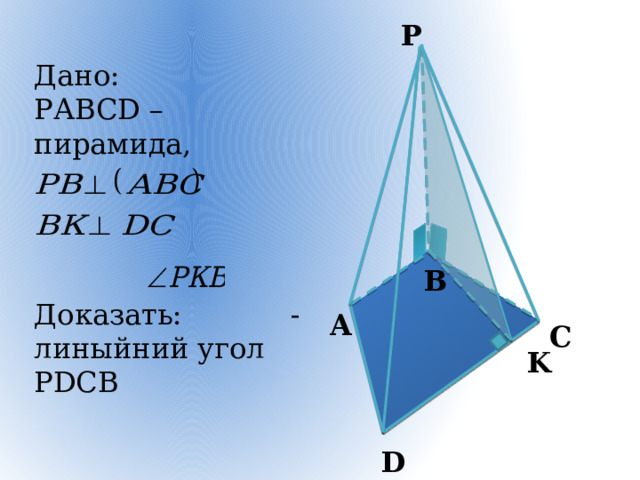
P
Дано:
РАВСD – пирамида,
Доказать: - линыйний угол РDСВ
B
A
C
K
D
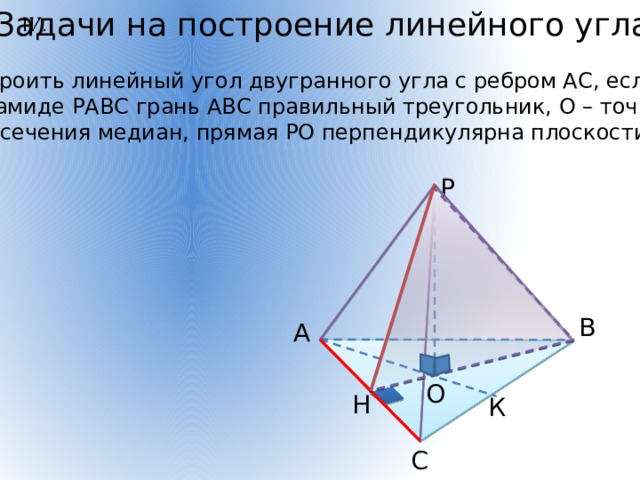
Задачи на построение линейного угла
Построить линейный угол двугранного угла с ребром АС, если в
пирамиде РАВС грань АВС правильный треугольник, О – точка
пересечения медиан, прямая РО перпендикулярна плоскости АВС.
Р
В
А
О
Н
К
С
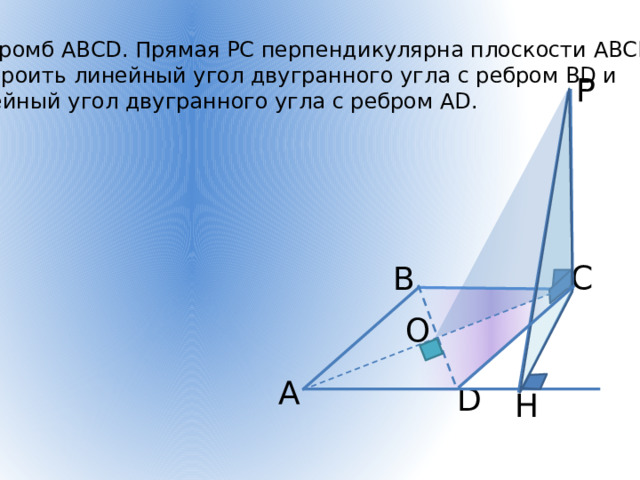
Дан ромб АВСD. Прямая РС перпендикулярна плоскости АВСD.
Построить линейный угол двугранного угла с ребром ВD и
линейный угол двугранного угла с ребром АD.
P
С
В
O
А
D
H
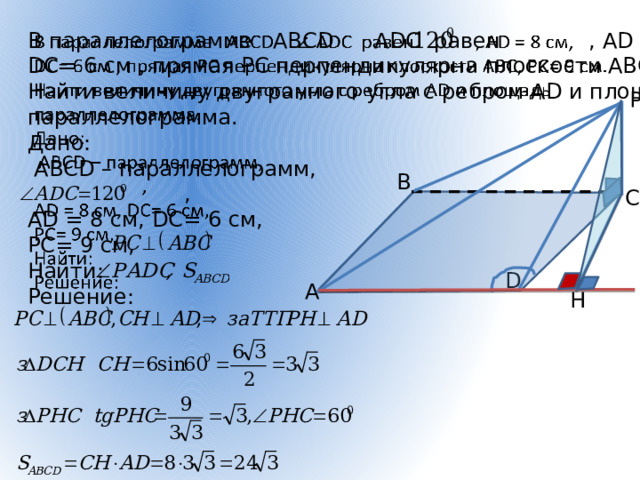
В параллелограмме АВСD АDС равен , АD = 8 см,
DС= 6 см , прямая РС перпендикулярна плоскости АВС, РС= 9 см.
Найти величину двугранного угла с ребром АD и площадь
параллелограмма.
Дано:
АВСD – параллелограмм,
,
АD = 8 см, DС= 6 см,
РС= 9 см,
Найти:
Решение:
P
В
С
D
А
H
15
































