

План урока:
1. Понятие цилиндра
2. Прямой круговой цилиндр и его элементы
3. Сечение цилиндра плоскостью
4. Площадь боковой и полной
поверхности цилиндра
5. Цилиндры вокруг нас
6. Проверочная работа
7. Домашнее задание
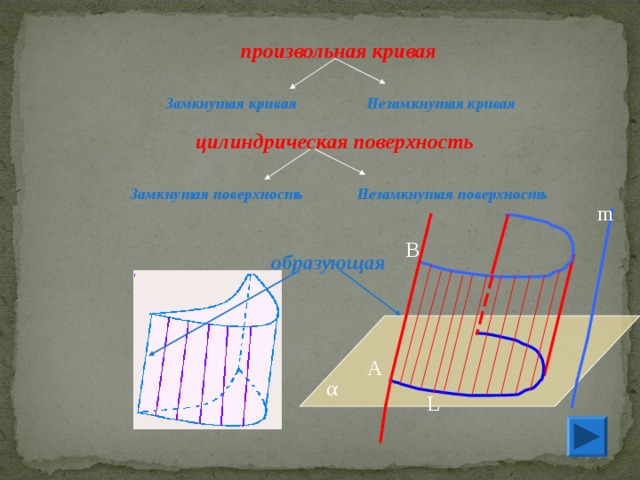
произвольная кривая
Замкнутая кривая
Незамкнутая кривая
цилиндрическая поверхность
Замкнутая поверхность
Незамкнутая поверхность
m
В
образующая
А
α
L
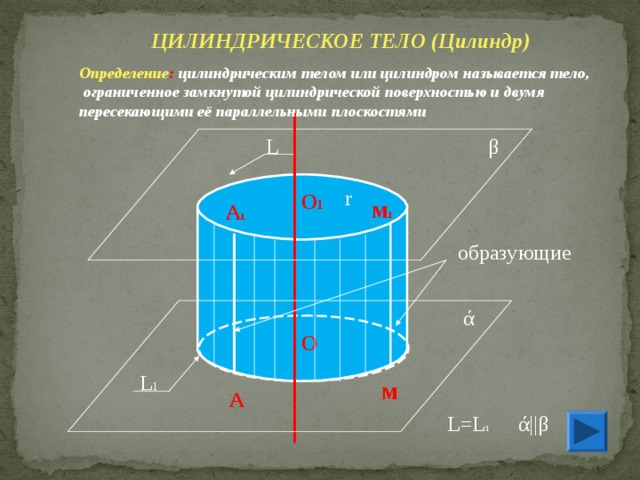
ЦИЛИНДРИЧЕСКОЕ ТЕЛО (Цилиндр)
Определение : цилиндрическим телом или цилиндром называется тело,
ограниченное замкнутой цилиндрической поверхностью и двумя
пересекающими её параллельными плоскостями
β
L
r
О 1
м 1
А 1
образующие
ά
О
L 1
м
А
L=L 1
ά || β
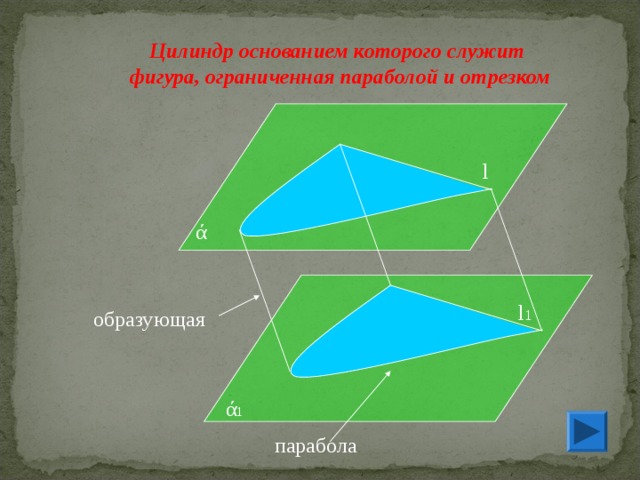
Цилиндр основанием которого служит
фигура, ограниченная параболой и отрезком
l
ά
l 1
образующая
ά 1
парабола
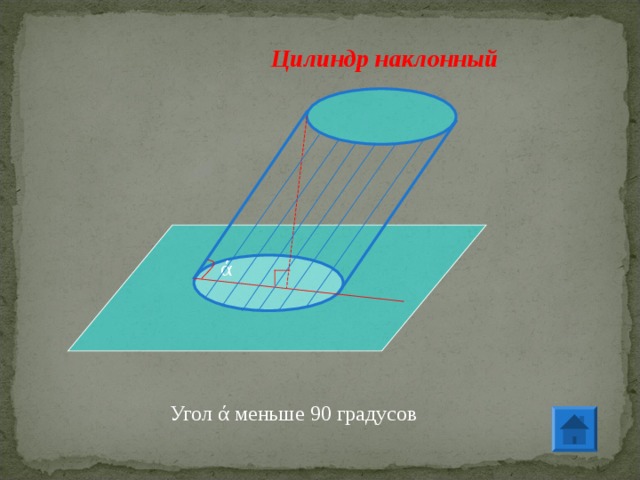
Цилиндр наклонный
ά
Угол ά меньше 90 градусов
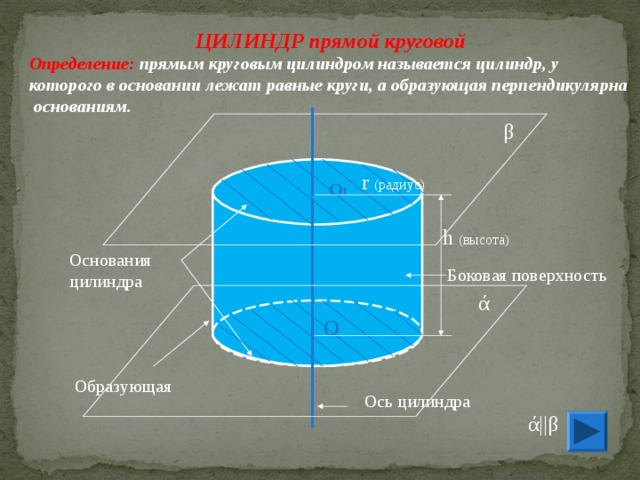
ЦИЛИНДР прямой круговой
Определение: прямым круговым цилиндром называется цилиндр, у
которого в основании лежат равные круги, а образующая перпендикулярна
основаниям.
β
r ( радиус)
О 1
h ( высота)
Основания
цилиндра
Боковая поверхность
ά
О
Образующая
Ось цилиндра
ά || β

1. Боковой поверхностью цилиндра называется часть
цилиндрической поверхности, заключенная между
параллельными плоскостями.
2. Основания - часть плоскостей, отсекаемых цилиндрической
поверхностью.
3. Радиусом цилиндра называется радиус его основания.
4. Высота цилиндра- расстояние между плоскостями оснований,
в прямом цилиндре она совпадает с образующей.
5. Ось цилиндра- прямая, проходящая через центры оснований,
она параллельна образующим.
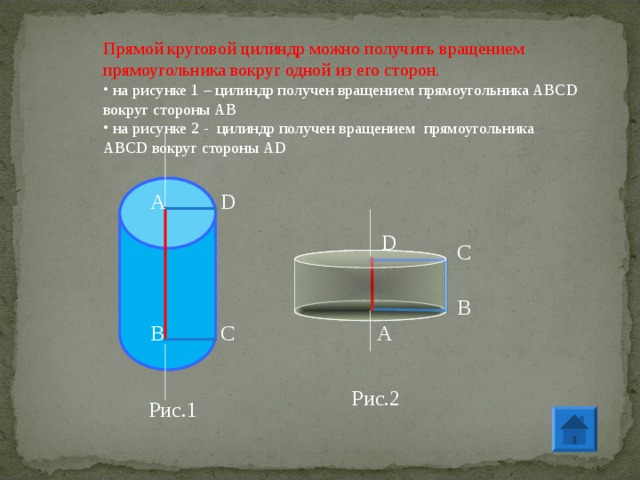
Прямой круговой цилиндр можно получить вращением
прямоугольника вокруг одной из его сторон.
- на рисунке 1 – цилиндр получен вращением прямоугольника АВС D
вокруг стороны АВ
- на рисунке 2 - цилиндр получен вращением прямоугольника
АВС D вокруг стороны AD
D
А
D
С
В
А
С
В
Рис.2
Рис.1
В
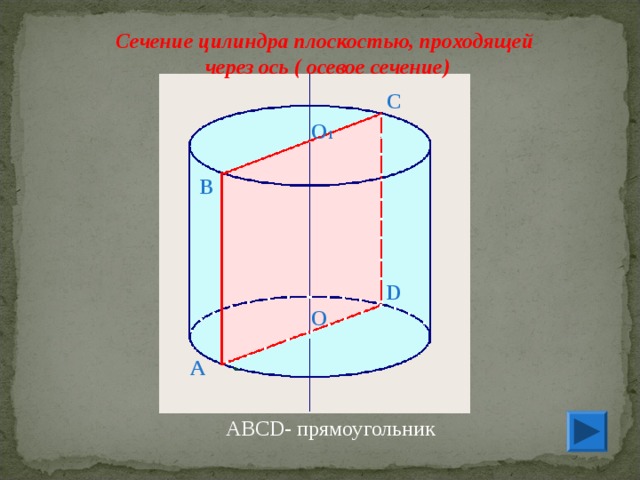
Сечение цилиндра плоскостью, проходящей
через ось ( осевое сечение)
С
О 1
D
О
А
АВС D - прямоугольник
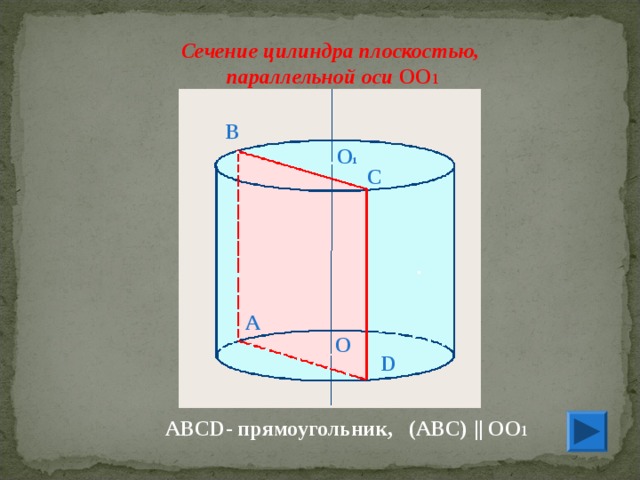
Сечение цилиндра плоскостью,
параллельной оси ОО 1
В
О 1
С
А
О
D
АВС D - прямоугольник, (ABC) || ОО 1
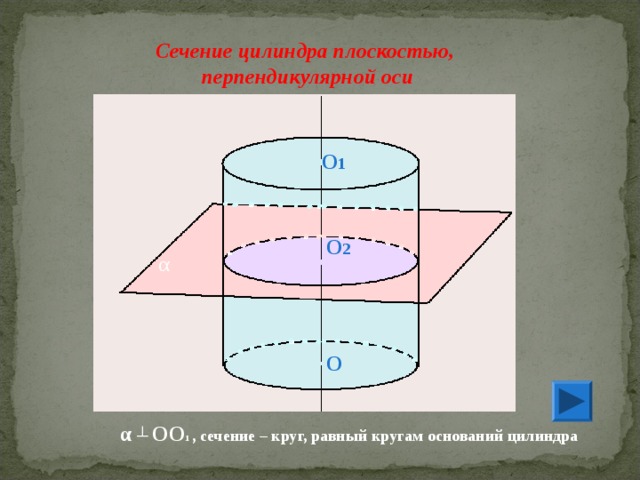
Сечение цилиндра плоскостью,
перпендикулярной оси
O 1
O 2
α
O
α ┴ OO 1 , сечение – круг, равный кругам оснований цилиндра

Сечение цилиндра плоскостью,
проходящей под углом к оси
о 1
α
α
о
Сечением является эллипс
/ α ≠ 90º
 S полн = 2 π rh + 2πr ² = 2π r ( r + h ) " width="640"
S полн = 2 π rh + 2πr ² = 2π r ( r + h ) " width="640"
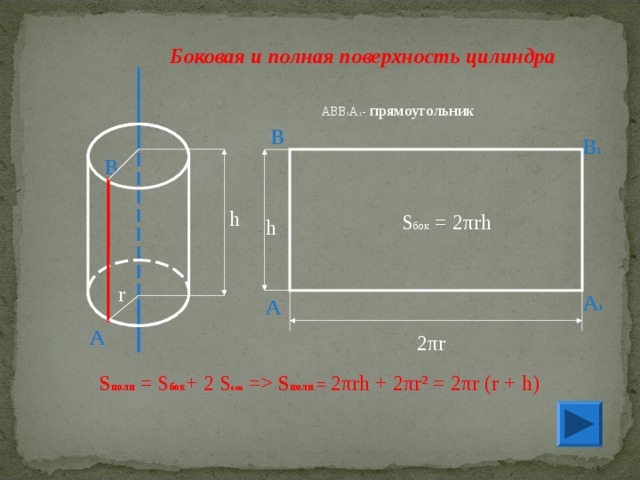
Боковая и полная поверхность цилиндра
АВВ 1 А 1 - прямоугольник
В
В 1
В
h
S бок = 2 π rh
h
r
А 1
А
А
2 π r
S полн = S бок + 2 S осн = S полн = 2 π rh + 2πr ² = 2π r ( r + h )
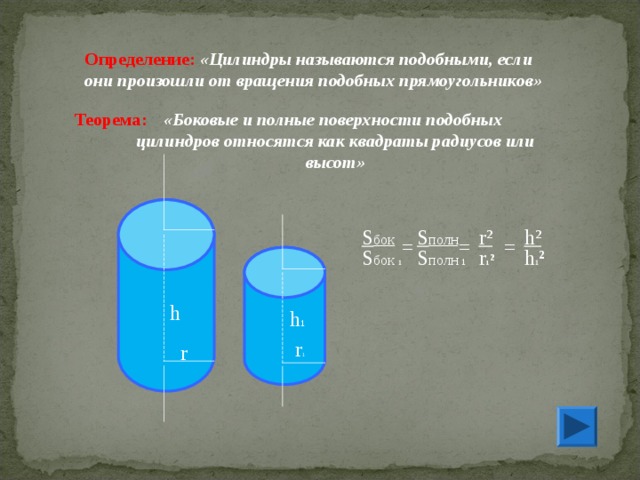
Определение: «Цилиндры называются подобными, если
они произошли от вращения подобных прямоугольников»
Теорема:
«Боковые и полные поверхности подобных
цилиндров относятся как квадраты радиусов или высот»
S бок
r²
h²
S полн
=
=
=
S бок 1
r 1 ²
h 1 ²
S полн 1
h
h 1
r 1
r

Внимание!

Задача
Второй вариант
Вычислите полную и боковую
поверхность цилиндра,
радиус которого равен 2 дм, а высота 6 дм
(ответ дать, не вычисляя значения π )
Первый вариант
Вычислите полную и боковую
поверхность цилиндра,
радиус которого равен 3 м, а высота 4 м
(ответ дать, не вычисляя значения π )

Историческая справка
Слово «цилиндр» происходит от греческого
слова « ΚΙΛΙΝΔΡΟΣ »,
что означает «валик», «каток».





















Ответь на вопросы
1. Назови элементы цилиндра
2.Назови вид осевого сечения цилиндра
3. Может ли сечение цилиндра быть:
- прямоугольником
- квадратом
- трапецией?
4.Какие из данных утверждений верны:
- любое сечение цилиндра плоскостью, перпендикулярной основанию есть окружность, равная окружности основания;
- любое сечение цилиндра плоскостью есть окружность, равная окружности основания;
- плоскость, перпендикулярная оси цилиндра, пересекает его по кругу, равному основанию цилиндра;
- сечением цилиндра могут быть круг, прямоугольник, эллипс.




















 S полн = 2 π rh + 2πr ² = 2π r ( r + h ) " width="640"
S полн = 2 π rh + 2πr ² = 2π r ( r + h ) " width="640"



































