Урок геометрии в 7 классе Решение задач по теме "Треугольники"

Тема урока: Решение задач по теме «Треугольники».

Тип урока: урок обобщения и систематизации знаний.

Цели урока:

Образовательные: организовать деятельность учащихся по применению знаний при решении задач на применение элементов треугольника; признаков равенства треугольников.

Развивающие:

- развитие ключевых компетенций;

- развитие навыков исследования через выполнение проектов по теме;

- формирование способности к оцениванию собственной деятельности.

Воспитательные: создать условия для

- формирования интереса учащихся к математике через углубление их представлений о практическом значении треугольников и применении их в окружающем мире;

- развитие деловых качеств личности, личностного самосовершенствования через представление проектов.

Задачи урока:

- учить учащихся грамотно вести монологическую речь;

- учить самостоятельной работе учащихся с различными источниками информации;

- учить использовать компьютерные информационные технологии для сопровождения собственного доклада или защиты результатов самостоятельной деятельности.

Необходимое оборудование и материалы:

компьютер;

экран;

проектор;

слайды;

дидактический материал

Межпредметные связи: география, литература, изо

Планируемые результаты:

личностные:

умение понимать смысл поставленной задачи, ясно и чётко излагать свои мысли в устной речи, выстраивать аргументацию, приводить контрпримеры;

опыт смыслообразования;

самооценка результатов деятельности, осознание границ применения нового знания;

умение работать в паре;

ценностно-эмоциональное отношение к изучаемому математическому содержанию с общекультурных позиций;

представление о значении математической науки как сфере человеческой деятельности;

метапредметные:

умение выделять главное, сравнивать, обобщать, проводить аналогию, применять индуктивные способы рассуждений, выдвигать гипотезы при решении учебных задач;

осознанное чтение текста;

способность к интерпретации;

представление о математике как средстве моделирования явлений окружающего мира;

предметные:

понятие треугольника;

умение использовать признаки равенства треугольников и строить речевые высказывания с использованием специальной терминологии;

умение устанавливать закономерность в применении признаков;

умение изображать геометрические фигуры;

использовать различные языки математики (словесный – символический – графический).

Структура урока

1. Организационный момент.

2. Постановка учебной проблемы.

3. Актуализация опорных знаний. Работа по готовым чертежам.

4. Обобщение и систематизация ключевых понятий.

5. Закрепление навыков решения практических задач.

6. Применение изучаемой темы в природе.

7. Задание на дом.

8. Подведение итогов урока.

9. Рефлексия

Ход урока:

1 Организационный момент.

Цель: формирование мотивации.

Здравствуйте! Меня зовут Дилара Сабировна, и эти 30 минут я буду вашим учителем математики. Ребята, я надеюсь, что этот урок пройдет интересно, с большой пользой для всех. Очень хочу, чтобы тот, кто еще равнодушен к царице всех наук, с нашего урока ушел с глубоким убеждением, что математика – интересный и нужный предмет.

Французский писатель XIX столетия Анатоль Франс однажды заметил: «Учиться можно только весело…. Чтобы переваривать знания, надо поглощать их с аппетитом» (слайд 3).

Давайте последуем совету писателя на сегодняшнем уроке: будьте активны, внимательны, поглощайте с большим желанием знания, которые пригодятся вам в дальнейшей жизни.

2. Постановка учебной проблемы.

Учитель: Ребята, при изучении темы «Треугольники» вы познакомились с понятием треугольника и с его видами - равнобедренный и равносторонний треугольник. Вряд ли кто-нибудь из вас не слышал о загадочном Бермудском треугольнике? (слайд 4). Это место, расположенное между Бермудскими островами, государством Пуэрто-Рико, полуостровом Флорида. А ещё его называют “дьявольский треугольник”, “треугольник проклятых”. Загадочность его заключается в чём? В том, что в нём бесследно исчезают корабли и самолёты. Природа “бермудского треугольника” остаётся тайной и посей день.

А ведь знакомый всем нам треугольник, который мы изучаем на уроках математики, также таит в себе немало интересного и загадочного.

Цель: формулирование цели урока

Учитель: Что нужно знать, на какие вопросы суметь ответить, чтобы получить полное представление о треугольнике? (слайд 5)

Учащиеся ставят проблемные вопросы и отвечают на них:

- Я думаю, мы должны знать, что называется треугольником? (слайд 6)

Учитель: Согласна. Так что же называется треугольником?

- А я думаю, что мы должны знать из чего состоит треугольник?

Учитель: Пожалуйста, перечисли элементы треугольника.

- Я предполагаю, что нам необходимо знать какие отрезки называются медианой, биссектрисой и высотой треугольника?

Учитель: Правильно. Дать определение медианы, биссектрисы и высотой треугольника.

- Я думаю, что необходимо знать, какие треугольники бывают? (по углам и сторонам) (слайд 7).

Учитель: И какие же?

Учитель. Правильно, ребята. А я хочу добавить вопросы, какими свойствами обладает равнобедренный треугольник? (слайд 8)

Какие треугольники называются равными и их признаки равенства? (слайд 9)

Учитель: Почему же так важно знать эти свойства? Я вам открою секрет: в материалах ГИА в задании № 15 есть задачи, которые мы научились решать уже сегодня. Пусть нынешний урок станет первым в подготовке к ГИА. (Слайд 8).

Цель: развитие пространственного мышления посредством решения задач на готовых чертежах.

Учитель: В повседневной жизни мы часто встречаемся с треугольником, используем его свойства, но! Одно дело иметь готовый чертеж и по нему работать, а другое, когда необходимо представить треугольник, его элементы и применить к воображаемому треугольнику свои знания. Другими словами нам с вами нужно иметь пространственное предсатвление, воображение, мышдение. Я предлагаю решить задачи, которые нам это помогут сделать.

Задание 1. На рисунке МP =MT, PK=TK какие точки достаточно соединить, чтобы получились равные треугольники? (слайд 10)

Задание 2. Проведите отрезок так, чтобы получились равные треугольники.

Проведите два отрезка так, чтобы получились равные треугольники. (слайд 11)

Задание 3. На рисунке даны две окружности с общим центром О и равные отрезки АВ и СD. Какие пары точек достаточно соединить, чтобы получились равные треугольники? (слайд 12)

4. Обобщение и систематизация ключевых понятий.

Цель: Применение исследовательских навыков при нахождении различных способов решения одной задачи.

Задача: На рисунке изображены два равных треугольника: ∆АВС=∆ВАD. Докажите, что ∆ АОС = ∆ ВОD. (слайд 13)

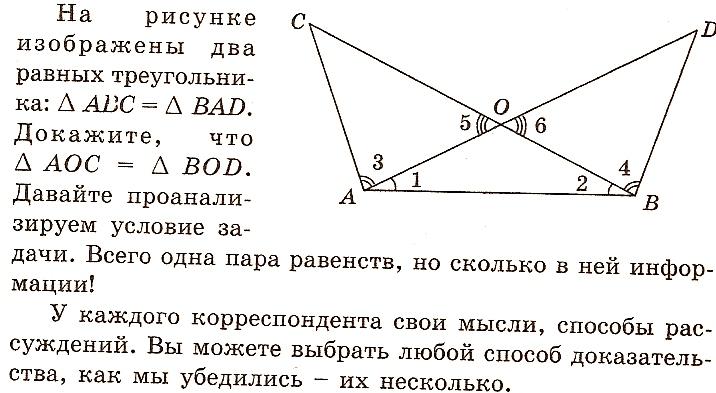
Учитель: Учитель: Ребята, исходные данные у всех были одинаковыми, и цель у всех была одна. А вот пути решения были разными. Давайте их рассмотрим.

Учащиеся указывают различные способы доказательства.

Учитель: Ребята, проведем небольшую физзарядку для глаз (слайд 14). Следим за движением геометрических фигур.

_______________________________________________________________

5.Закрепление навыков решения практических задач.

Цель: Ознакомление с историей развития математики, применение знаний при решении практической задачи.

Учитель: Ребята, при решении последней задачи вы использовали такой приём, как – доказательство. Эта форма работы вам ещё недостаточно хорошо известна. А до VI века н.э. с доказательством люди вообще были не знакомы.

Первым ученым, который стал рассуждать, доказывать был Фалес Милетский.

Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. Одним из самых известных его высказываний было «Познай самого себя».

Послушаем ________________, который подготовил небольшое сообщение о Фалесе.

___________ (Слайд 15). Первым, кто начал получать новые геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик Фалес, который жил в VI в. до н. э. Ему принадлежит открытие следующих теорем: вертикальные углы равны; в равнобедренном треугольнике углы, лежащие при основании, равны; Теорема о равенстве двух треугольников по стороне и двум прилежащим к ней углам.

(Слайд 16). Теореме о равенстве треугольников по двум сторонам и углу между ними Фалес нашел практическое приложение

В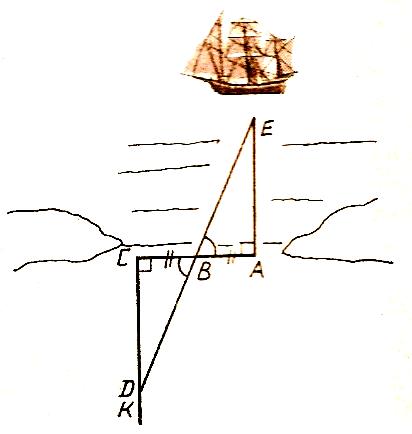 гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В, С, (АВ = ВС) и размеченную прямую 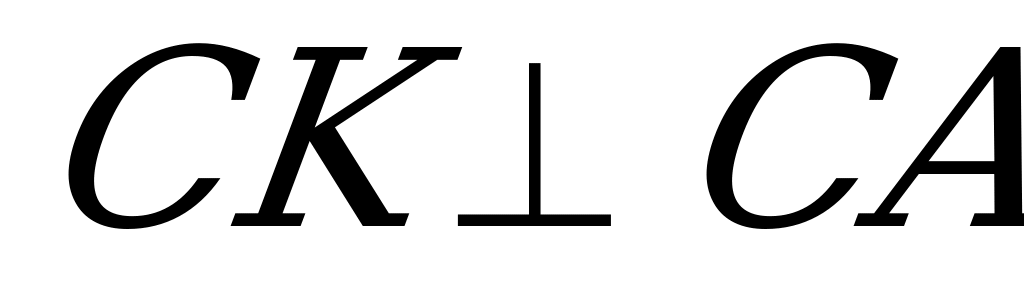. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, В, Е оказывались на одной прямой. Как ясно из чертежа, расстояние на земле СD и является искомым расстоянием до корабля АЕ по воде

Учитель: В нашей местности немало озер. Решение следующей задачи позволит вам научиться определять ширину любого озера.

З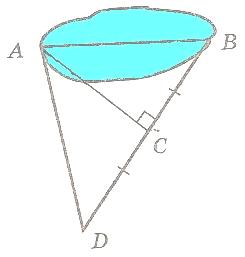 адача (слайд 17): Чтобы измерить длину озера (расстояние АВ на рисунке) на местности провели прямою ВD, на ней выбрали точку C, из которой точка А видна под прямым углом, и отложили отрезок СD, равный отрезку ВC. Какое расстояние на местности надо измерить, чтобы узнать длину озера?

Учащиеся: Для этого достаточно измерить длину отрезка АD, так как ∆АСD=∆ВСА (по первому признаку).

6. Применение изучаемой темы в природе.

Цель: формирование причинно-следственных связей.

Учитель: Ребята, математика связана с красотой окружающего нас мира. Например, мир природы и симметрии. Искусство и математика, в частности архитектура, скульптура, изобразительное искусство. На нашем уроке мы узнаем два новых понятия, которые никогда не узнало бы человечество, если бы в VI веке до нашей эры Фалес Милетский не ввел понятие равнобедренного треугольника и не попытался доказать его свойства. Но прежде, вашему вниманию будет представлена с одной стороны простая, а с другой очень интересная и красивая геометрически, а также интересная и для науки геометрическая система, которая состоит из равнобедренных и равносторонних треугольников.

В ходе изучения темы вам были заданы проблемные вопросы, на которые вы должны были найти ответы (слайд 18):

1. Фракталы? Их связь с геометрией.

2. Что мы знаем о Спидронах и Снежинке Коха?

Учитель: Итак, что такое фрактал? Бенуа Мандельброт создал неевклидову геометрию негладких, шероховатых, зазубренных, объектов. По его мнению, именно «неправильные» объекты составляют подавляющее большинство объектов в природе. ________________ расскажет нам о фракталах.

Красота фракталов сочетает в себе красоту симметричных объектов типа кристаллов с красотой «живых», природных объектов, привлекательных именно своей неправильностью.

Учитель: И еще одно не менее интересное понятие, которое возникло совсем недавно, но также интересно и красиво - это Спидрон. __________ подготовил мини-проект о спидронах.

Учитель: Снежинка Коха является родственницей целого класса фигур, которые получили название Фракталы. Основной фигурой, которая участвовала в построении фракталов, являлся равнобедренный треугольник, впоследствии теория фракталов была развита и получила широкое применение не только в геометрии, но и в других отраслях и сейчас мы об этом узнаем из сообщения __________.

Учитель: Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть новые элементы прекрасного, которые находят свое применение в окружающем нас мире. Так в чем же заключается уникальность треугольника? Людей с давних времен волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким-либо математическим расчетам. Можно ли «проверить алгеброй гармонию?»- как сказал А.С.Пушкин.

Я предлагаю вам, ребята, на время представить себя Мандельбротом, Кохом и выполнить практическое задание: собрать из 4 треугольников: 1 группа - равнобедренный, 2 группа – тупоугольный, 3 группа – прямоугольный, 4 группа – равносторонний.

Задание на дом (слайд 19).

Цель: Развитие творческих и изобретательских способностей учащихся.

Учащимся предлагается дома выполнить домашнее задание с опорой на проблемный вопрос урока.

1. Четыре страны имеют форму треугольников. Как расположены страны одна относительно другой, если у каждой из них есть общие границы с тремя другими? Нарисуйте.

2) Из треугольника, разрезанного на меньшие треугольники собрать различные рисунки (можно собрать кошку, рыбку и робота).

3) Творческая группа: написать мини-сочинение «Для чего изучаем геометрию мы?».

Учитель: Я думаю, что и в дальнейшем людей будет интересовать равнобедренный и равносторонний треугольники. И из таких простых слагаемых, может быть кто-нибудь из вас, составит ещё более интересную, более сложную, более многогранную сумму и назовет это новое чудо природы еще более интересным и замечательным словом. Я благодарна вам за активное участие на уроке. «5» _________________________________ за подготовку сообщений, защиту проектов, также _____________________________ за решение практических задач.

«4» _____________________________________. Ребята, вы хорошо проработали на уроке, но вам необходимо повторить теорию.

Цель: Развитие рефлексивной деятельности

Рефлексия (Слад 20):

Учитель: Сегодня на занятии мы учились смотреть и видеть, замечать различные особенности геометрической фигуры - треугольника, правильно мыслить и рассуждать. Рассмотрели различные виды треугольников. Мы встретились с занимательными задачами и геометрическими играми, которые развивают усидчивость и аккуратность.

С помощью геометрии мы можем решить многие задачи и ответить на многие вопросы. В свое время Галилео Галилей говорил, что «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Я вам заготовила развертку тетраэдра. Дома, ребята склейте по изгибам, и у вас получится тетраэдр, который вам будет напоминать о нашем уроке и он пригодится при изучении геометрии в 10 классе.

Удачи вам, ребята! (слайд 21). Спасибо за урок!

2.Собрать треугольник из 4 частей.

1 группа (равнобедренный)

2 группа (тупоугольный)

3 группа (прямоугольный)

4 группа (равносторонний)